
例1.某厂2001年生产利润逐月增加,且每月增加的利润相同,但由于厂方正在改造建设,元月份投入资金建设恰好与元月的利润相等,随着投入资金的逐月增加,且每月增加投入的百分率相同,到12月投入建设资金又恰好与12月的生产利润相同,问全年总利润m与全年总投入N的大小关系是 ( )
A. m>N B. m<N C.m=N D.无法确定
[分析]每月的利润组成一个等差数列{an},且公差d>0,每月的投资额组成一个等比数列{bn},且公比q>1。 ,且
,且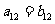 ,比较
,比较 与
与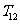 的大小。
的大小。
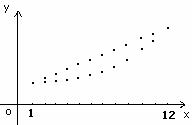
若直接求和,很难比较出其大小,但注意到等差数列的通项公式an=a1+(n-1)d是关于n的一次函数,其图象是一条直线上的一些点列。等比数列的通项公式bn=a1qn-1是关于n的指数函数,其图象是指数函数上的一些点列。
在同一坐标系中画出图象,直观地可以看出ai≥bi 则 >
>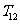 ,即m>N。
,即m>N。
[点评]把一个原本是求和的问题,退化到各项的逐一比较大小,而一次函数、指数函数的图象又是每个学生所熟悉的。在对问题的化归过程中进一步挖掘了问题的内涵,通过对问题的反思、再加工后,使问题直观、形象,使解答更清新。

例2.如果,三棱锥P-ABC中,已知PA⊥BC,PA=BC=l,PA,BC的公垂线ED=h.求证三棱锥P-ABC的体积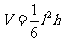 .
.
分析:如视P为顶点,△ABC为底面,则无论是S△ABC以及高h都不好求.如果观察图形,换个角度看问题,创造条件去应用三棱锥体积公式,则可走出困境.
解:如图,连结EB,EC,由PA⊥BC,PA⊥ED,ED∩BC=E,可得PA⊥面ECD.这样,截面ECD将原三棱锥切割成两个分别以ECD为底面,以PE、AE为高的小三棱锥,而它们的底面积相等,高相加等于PE+AE=PA=l,所以
VP-ABC=VP-ECD+VA-ECD=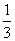 S△ECD•AE+
S△ECD•AE+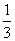 S△ECD•PE=
S△ECD•PE=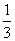 S△ECD •PA=
S△ECD •PA=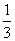 •
• BC·ED·PA=
BC·ED·PA=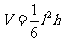 .
. 评注:辅助截面ECD的添设使问题转化为已知问题迎刃而解.
评注:辅助截面ECD的添设使问题转化为已知问题迎刃而解.
例3.在 的展开式中x的系数为( ).
的展开式中x的系数为( ).
(A)160 (B)240 (C)360 (D)800
分析与解:本题要求 展开式中x的系数,而我们只学习过多项式乘法法则及二项展开式定理,因此,就要把对x系数的计算用上述两种思路进行转化:
展开式中x的系数,而我们只学习过多项式乘法法则及二项展开式定理,因此,就要把对x系数的计算用上述两种思路进行转化:
思路1:直接运用多项式乘法法则和两个基本原理求解,则 展开式是一个关于x的10次多项式,
展开式是一个关于x的10次多项式, =(x2+3x+2) (x2+3x+2) (x2+3x+2)
(x2+3x+2) (x2+3x+2),它的展开式中的一次项只能从5个括号中的一个中选取一次项3x并在其余四个括号中均选 择常数项2相乘得到,故为
=(x2+3x+2) (x2+3x+2) (x2+3x+2)
(x2+3x+2) (x2+3x+2),它的展开式中的一次项只能从5个括号中的一个中选取一次项3x并在其余四个括号中均选 择常数项2相乘得到,故为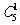 ·(3x)·
·(3x)·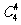 ·24=5×3×16x=240x,所以应选(B).
·24=5×3×16x=240x,所以应选(B).
思路2 利用二项式定理把三项式乘幂转化为二项式定理再进行计算,∵x2+3x+2=x2+ (3x+2)=(x2+2)+3x=(x2+3x)+2=(x+1)(x+2)=(1+x)(2+x),∴这条思路下又有四种不同的化归与转化方法.①如利用x2+3x+2=x2+(3x+2)转化,可以发现只有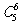 (3x+2)5中会有x项,即
(3x+2)5中会有x项,即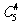 (3x)·24=240x,故选(B);②如利用x2+3x+2= (x2+2)+3x进行转化,则只
(3x)·24=240x,故选(B);②如利用x2+3x+2= (x2+2)+3x进行转化,则只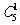 (x2+2) 4·3x中含有x一次项,即
(x2+2) 4·3x中含有x一次项,即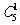 ·3x·C44·24=240x;③如利用x2+3x+2=(x2+3x)+2进行转化,就只有
·3x·C44·24=240x;③如利用x2+3x+2=(x2+3x)+2进行转化,就只有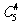 ·(x2+3x)·24中会有x项,即240x;④如选择x2+3x+2=(1+x)(2+x)进行转化,
·(x2+3x)·24中会有x项,即240x;④如选择x2+3x+2=(1+x)(2+x)进行转化, =
=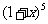 ×
×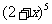 展开式中的一次项x只能由(1+x)5中的一次项乘以(2+x)5展开式中的常数项加上(2+x)5展开式中的一次项乘以(1+x)5展开式中的常数项后得到,即为
展开式中的一次项x只能由(1+x)5中的一次项乘以(2+x)5展开式中的常数项加上(2+x)5展开式中的一次项乘以(1+x)5展开式中的常数项后得到,即为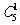 x·
x·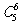 25+
25+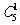 •24•x•
•24•x•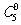 •15=160x+80x=240x,故选(B).
•15=160x+80x=240x,故选(B).
评注:化归与转化的意识帮我们把未知转化为已知。
例4.若不等式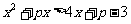 对一切
对一切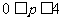 均成立,试求实数
均成立,试求实数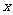 的取值范围。
的取值范围。
解:
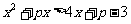
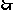
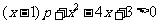
令
 ,则要使它对
,则要使它对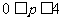 均有
均有 ,只要有
,只要有
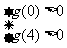
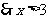 或
或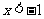 。
。
点评:在有几个变量的问题中,常常有一个变元处于主要地位,我们称之为主元,由于思维定势的影响,在解决这类问题时,我们总是紧紧抓住主元不放,这在很多情况下是正确的。但在某些特定条件下,此路往往不通,这时若能变更主元,转移变元在问题中的地位,就能使问题迎刃而解。本题中,若视x为主元来处理,既繁且易出错,实行主元的转化,使问题变成关于p的一次不等式,使问题实现了从高维向低维转化,解题简单易行。
4.化归与转化应遵循的基本原则:
(1)熟悉化原则:将陌生的问题转化为熟悉的问题,以利于我们运用熟知的知识、经验和问题来解决。
(2)简单化原则:将复杂的问题化归为简单问题,通过对简单问题的解决,达到解决复杂问题的目的,或获得某种解题的启示和依据。
(3)和谐化原则:化归问题的条件或结论,使其表现形式更符合数与形内部所表示的和谐的形式,或者转化命题,使其推演有利于运用某种数学方法或其方法符合人们的思维规律。
(4)直观化原则:将比较抽象的问题转化为比较直观的问题来解决。
(5)正难则反原则:当问题正面讨论遇到困难时,可考虑问题的反面,设法从问题的反面去探求,使问题获解。
3.转化有等价转化和非等价转化。等价转化前后是充要条件,所以尽可能使转化具有等价性;在不得已的情况下,进行不等价转化,应附加限制条件,以保持等价性,或对所得结论进行必要的验证。
2.化归与转化思想的实质是揭示联系,实现转化。除极简单的数学问题外,每个数学问题的解决都是通过转化为已知的问题实现的。从这个意义上讲,解决数学问题就是从未知向已知转化的过程。化归与转化的思想是解决数学问题的根本思想,解题的过程实际上就是一步步转化的过程。数学中的转化比比皆是,如未知向已知转化,复杂问题向简单问题转化,新知识向旧知识的转化,命题之间的转化,数与形的转化,空间向平面的转化,高维向低维转化,多元向一元转化,高次向低次转化,超越式向代数式的转化,函数与方程的转化等,都是转化思想的体现。
1.解决数学问题时,常遇到一些问题直接求解较为困难,通过观察、分析、类比、联想等思维过程,选择运用恰当的数学方法进行变换,将原问题转化为一个新问题(相对来说,对自己较熟悉的问题),通过新问题的求解,达到解决原问题的目的,这一思想方法我们称之为“化归与转化的思想方法”。
15. 设a>0且 ,试求使方程
,试求使方程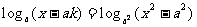 有解的k的取值范围。
有解的k的取值范围。

14. 已知椭圆的中心在原点,集点在坐标轴上,焦距为 ,另一双曲线与此椭圆有公共焦点,且其实轴比椭圆的长轴小8,两曲线的离心率之比为3:7,求此椭圆、双曲线的方程。
,另一双曲线与此椭圆有公共焦点,且其实轴比椭圆的长轴小8,两曲线的离心率之比为3:7,求此椭圆、双曲线的方程。
13. 不等式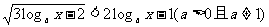 的解集为_____________。
的解集为_____________。
12. 在50件产品中有4件是次品,从中任抽取5件,至少有3件次品的抽法共有______________种(用数字作答)
11. 与圆 相切,且在两坐标轴上截距相等的直线方程为____________。
相切,且在两坐标轴上截距相等的直线方程为____________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com