
2. 已知x , y为正实数, 且x、a1、a2、y成等差数列, x、b1、b2、y成等比数列, 则 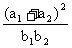
的取值范围是 ( )
A. R
B. 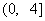 C.
C.
 D.
D.
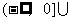

1. 在项数为2n+1的等差数列中, 所有奇数项和与所有偶数项和之比为 ( )
A. 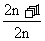 B.
B.
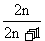 C.
C.
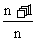 D.
D.
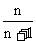
14. 解: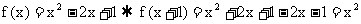 ,
,
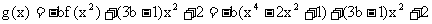 ,
,
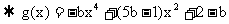 ,
,
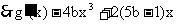 , 当
, 当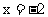 时
时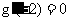
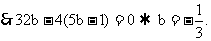
13. 解:(1)设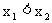 ,
, 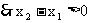 , 当
, 当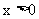 时,
时, 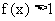 ,
,
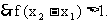
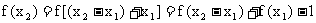
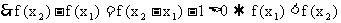
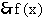 在R上为增函数
在R上为增函数
(2) 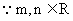 , 不妨设
, 不妨设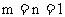
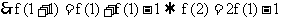
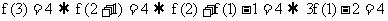
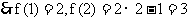
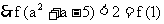 ,
, 
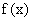 在R上为增函数
在R上为增函数
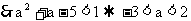
即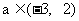
12. 解: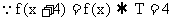 ,
, 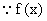 为奇函数,
为奇函数,
当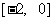 时,
时, 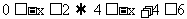
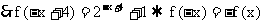
得: 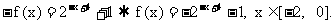
11. 解:当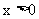 时,
时,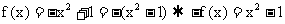
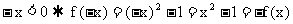
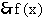 在
在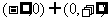 上为奇函数.
上为奇函数.
7. 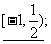 8.
8.  9.
9. 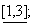 10.
10. 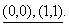
(二) 专题测试与练习
(一) 典型例题
例1 C.
例2 解: (1) 
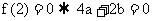 , 由
, 由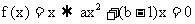

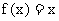 有等根,
有等根, 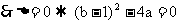
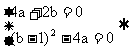 得:
得: 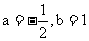
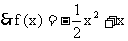
(2) 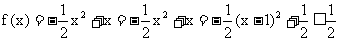 ,
,
则有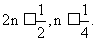
又二次函数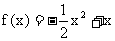 的对称轴为直线
的对称轴为直线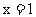 ,
,
∴ 解得:
解得: 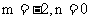
∴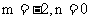 .
.
例3解: (1)
先求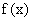 在
在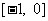 上的解析式
上的解析式
设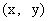 是
是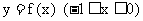 上的一点,
上的一点,
则点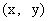 关于
关于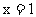 的对称点为
的对称点为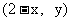 且
且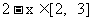
所以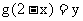 得
得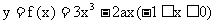 .
.
再根据偶函数的性质, 求当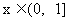 上的解析式为
上的解析式为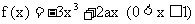
所以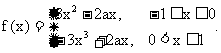
(2) 当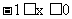 时,
时, 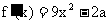
因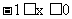 时, 所以
时, 所以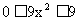
因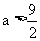 , 所以
, 所以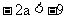 , 所以
, 所以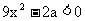 而
而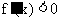 . 所以
. 所以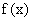 在
在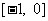 上为减函数.
上为减函数.
当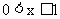 时,
时, 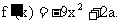 因
因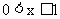 , 所以
, 所以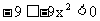
因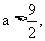 所以
所以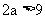 , 所以
, 所以 , 即
, 即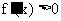
所以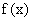 在
在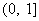 上为增函数
上为增函数
(3) 由(2)知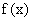 在
在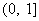 上为增函数,在
上为增函数,在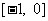 上为减函数,
上为减函数,
又因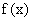 为偶函数, 所以
为偶函数, 所以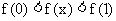
所以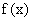 在
在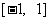 上的最大值
上的最大值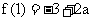
由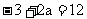 得
得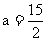 .
.
11. 用定义判断函数f (x )=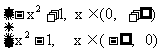 的奇偶性
的奇偶性
12. 设奇函数f (x )的定义域为R , 且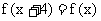 , 当x
, 当x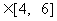 时f (x)=
时f (x)=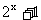 , 求f (x )
, 求f (x )
在区间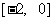 上的表达式.
上的表达式.
13. 函数f (x )对任意的m、n∈R, 都有f (m+n )=f (m)+f (n)-1, 并且x>0时, 恒有f (x )>1.
(1) 求证: f (x )在R上是增函数; (2 ) 若f (3 )=4, 解不等式f ( )<2.
)<2.
14. 已知函数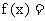
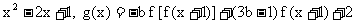 在区间
在区间
 上是减函数, 且在区间
上是减函数, 且在区间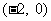 上是增函数, 求实数b的值.
上是增函数, 求实数b的值.
函数的单调性与奇偶性解答
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com