
17. 将3k(k为正整数)个石子分成五堆.如果通过每次从其中3堆中各取走一个石子,而最后取完,则称这样的分法是“和谐的”.试给出和谐分法的充分必要条件,并加以证明.
解: 分法是和谐的 充分必要条件 是 最多一堆石子的个数不超过k.………(5分)
下面设五堆石子的个数分别为a,b,c,d,e(其中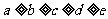 ).
).
“必要性”的证明: 若分法是和谐的,则把a所对应的石子取完至少要取a次,这a次每次都要取走3个石子.如果 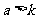 ,则
,则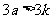 ,即把a所对应的一堆取完时,需取走的石子多于五堆石子的总数.矛盾.因此最多一堆石子的个数不能超过k.…………………(15分)
,即把a所对应的一堆取完时,需取走的石子多于五堆石子的总数.矛盾.因此最多一堆石子的个数不能超过k.…………………(15分)
“充分性”的证明:(数学归纳法)
(1) 当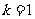 时,满足“
时,满足“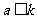 ” 的分法只能是1,1,1,0,0.显然这样的分法是和谐的.
” 的分法只能是1,1,1,0,0.显然这样的分法是和谐的.
(2) 假设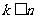 时,满足“
时,满足“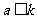 ” 的分法是和谐的.
” 的分法是和谐的.
(3) 当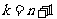 时,若
时,若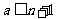 ,且分法a,b,c,d,e是不和谐的,则分法a-1,b-1,c-1, d, e也是不和谐的.由(2)及必要性的证明,可知
,且分法a,b,c,d,e是不和谐的,则分法a-1,b-1,c-1, d, e也是不和谐的.由(2)及必要性的证明,可知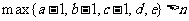 .
.
因为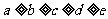 ,所以
,所以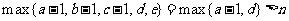 .
.
若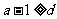 ,则有
,则有 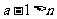 .这与
.这与 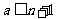 矛盾.
矛盾.
若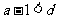 ,则有
,则有 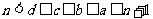 ,从而有
,从而有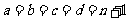 ,于是有
,于是有
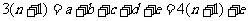 ,这是不可能的.矛盾.
,这是不可能的.矛盾.
因此当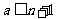 时,分法a,b,c,d,e是和谐的.…………………………………………(25分)
时,分法a,b,c,d,e是和谐的.…………………………………………(25分)
16.设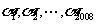 为2008个整数,且
为2008个整数,且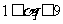 (
(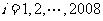 ).如果存在某个
).如果存在某个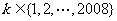 ,使得2008位数
,使得2008位数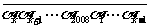 被101整除,试证明:对一切
被101整除,试证明:对一切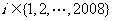 ,2008位数
,2008位数 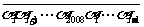 均能被101整除.
均能被101整除.
解: 根据已知条件,不妨设k=1,即2008位数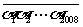 被101整除,只要能证明2008位数
被101整除,只要能证明2008位数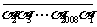 能被101整除. ……………………(5分)
能被101整除. ……………………(5分)
事实上,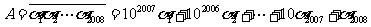 ,
,
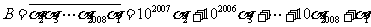 ……………………(10分)
……………………(10分)
从而有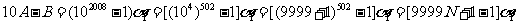 ,
,
即有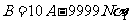 .……………………(20分)
.……………………(20分)
因为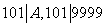 ,所以
,所以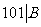 . 利用上述方法依次类推可以得到
. 利用上述方法依次类推可以得到
对一切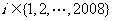 ,2008位数
,2008位数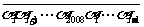 均能被101整除.……(25分)
均能被101整除.……(25分)
15.设非负等差数列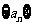 的公差
的公差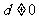 ,记
,记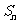 为数列
为数列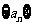 的前n项和,证明:
的前n项和,证明:
(1)若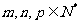 ,且
,且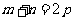 ,则
,则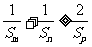 ;
;
(2)若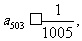 则
则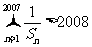 。
。
解:设非负等差数列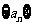 的首项为
的首项为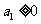 ,公差为
,公差为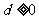 .
.
(1)因为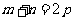 ,所以
,所以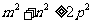 ,
,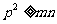 ,
,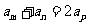 .
.
从而有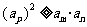 . 因为
. 因为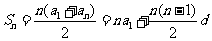 ,所以有
,所以有
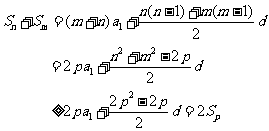 ……………………(5分)
……………………(5分)

于是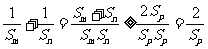 . ……………………(10分)
. ……………………(10分)
(2) 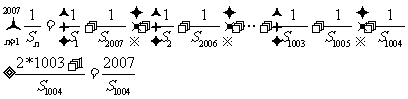 ………(15分)
………(15分)
又因为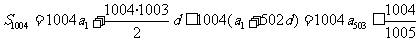 ,所以有
,所以有
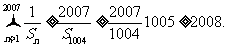 …………………………………………(20分)
…………………………………………(20分)
14.求解不等式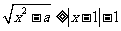 。
。
解:(I)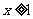 情形.此时不等式为
情形.此时不等式为 .于是有
.于是有
(1) .
.
因此 当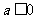 时,有
时,有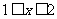 ;当
;当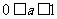 时,有
时,有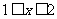 ;
;
当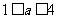 时,有
时,有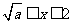 ;当
;当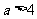 时,空集. …………………… (5分)
时,空集. …………………… (5分)
(2)  .
.
此时有 当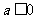 时,有
时,有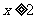 ;当
;当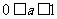 时,有
时,有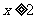 ;当
;当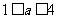 时,有
时,有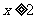 ;当
;当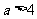 时,
时,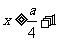 .
…………………………………………(10分)
.
…………………………………………(10分)
(II)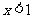 情形.此时不等式为
情形.此时不等式为 .
.
于是有
(3) .
.
因此 当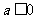 时,有
时,有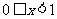 ;当
;当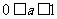 时,有
时,有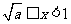 ;当
;当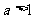 时,空集.……(15分)
时,空集.……(15分)
(4) .
.
因此 当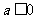 时,有
时,有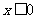 ;当
;当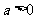 时,空集.
时,空集.
综合(1)-(4)可得
当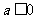 时,有
时,有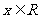 ;当
;当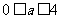 时,有
时,有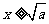 ;当
;当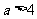 时,
时,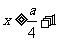 .…(20分)
.…(20分)
13.已知椭圆C: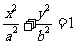 (
(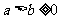 ),其离心率为
),其离心率为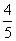 ,两准线之间的距离为
,两准线之间的距离为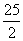 。(1)求
。(1)求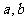 之值;(2)设点A坐标为(6, 0),B为椭圆C上的动点,以A为直角顶点,作等腰直角△ABP(字母A,B,P按顺时针方向排列),求P点的轨迹方程。
之值;(2)设点A坐标为(6, 0),B为椭圆C上的动点,以A为直角顶点,作等腰直角△ABP(字母A,B,P按顺时针方向排列),求P点的轨迹方程。
解:(1)设c为椭圆的焦半径,则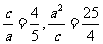 . ……………………(5分)
. ……………………(5分)
于是有a=5,b=3.
(2) 解法一:设B点坐标为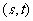 ,P点坐标为
,P点坐标为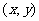 .于是有
.于是有
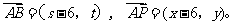
因为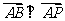 ,所以有
,所以有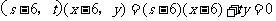 .
(A1 )
.
(A1 )
又因为ABP为等腰直角三角形,所以有 AB=AP,即
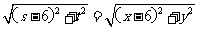 .
(A2 ) …………(10分)
.
(A2 ) …………(10分)
由(A1)推出 ,代入(A2),得
,代入(A2),得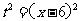 ……(15分)
……(15分)
从而有 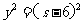 ,即
,即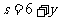 (不合题意,舍去)或
(不合题意,舍去)或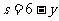 .
.
代入椭圆方程,即得动点P的轨迹方程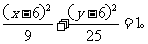 …………(20分)
…………(20分)
解法二: 设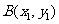 ,
,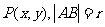 ,则以A为圆心,r为半径的圆的参数方程为
,则以A为圆心,r为半径的圆的参数方程为
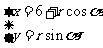 .
.
设AB与x轴正方向夹角为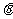 ,B点的参数表示为
,B点的参数表示为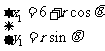 , …………(10分)
, …………(10分)
P点的参数表示为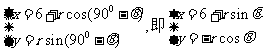 .
.
从上面两式,得到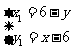 . ……………………(15分)
. ……………………(15分)
又由于B点在椭圆上,可得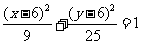 . ……………………(20分)
. ……………………(20分)
此即为P点的轨迹方程.
12.在边长为1的正三角形ABC的边AB、AC上分别取D、E两点,使沿线段DE折叠三角形时,顶点A正好落在边BC上.AD的长度的最小值为 .
解:设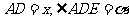 ,作△ADE关于DE的对称图形,A的对称点G落在BC上.在△DGB中,
,作△ADE关于DE的对称图形,A的对称点G落在BC上.在△DGB中,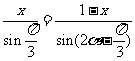
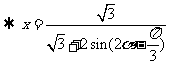
当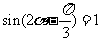 时,即
时,即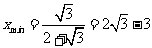 .
.
11.已知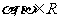 ,直线
,直线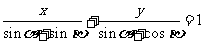 与
与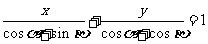
的交点在直线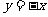 上,则
上,则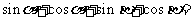 .
.
解:由已知可知,可设两直线的交点为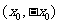 ,且
,且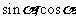 为方程
为方程
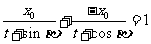 ,
,
的两个根,即为方程
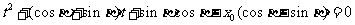
的两个根.因此
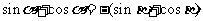 ,
,
即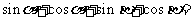 0.
0.
10. 设实系数一元二次方程 有两个相异实根,其中一根在区间
有两个相异实根,其中一根在区间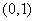 内,另一根在区间
内,另一根在区间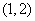 内,则
内,则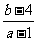 的取值范围是
.
的取值范围是
.
解: 根据题意,设两个相异的实根为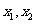 ,且
,且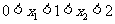 ,则
,则
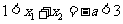 ,
,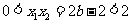 .
.
于是有 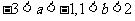 ,也即有
,也即有
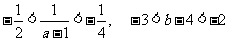 .
.
故有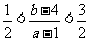 ,即取值范围为
,即取值范围为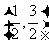 .
.
9.设 ,则
,则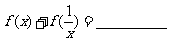 .
.
解: 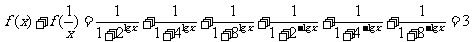 .
.
8.设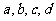 为非负实数,满足
为非负实数,满足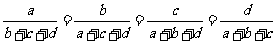 ,则
,则
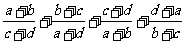 =
.
=
.
解:显然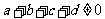 ,由于
,由于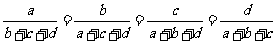 ,有
,有
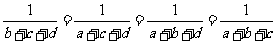 .于是有
.于是有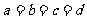 ,故
,故
 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com