
5. 若函数y=x 3-2x 2+mx, 当x=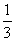 时, 函数取得极大值, 则m的值为
( )
时, 函数取得极大值, 则m的值为
( )
A. 3
B. 2
C. 1
D. 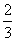
4. 已知函数y=-x 2-2x+3在区间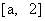 上的最大值为
上的最大值为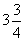 , 则a等于
( )
, 则a等于
( )
A. -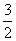 B.
B. 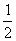 C. -
C. -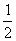 D. -
D. -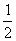 或-
或-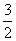
3. 函数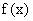 =
=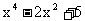 在区间
在区间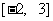 上的最大值与最小值分别是
( )
上的最大值与最小值分别是
( )
A. 5, 4 B. 13, 4 C. 68, 4 D. 68, 5
2. 已知某物体的运动方程是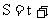
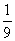
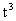 , 则当
, 则当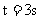 时的瞬时速度是
( )
时的瞬时速度是
( )
A. 10m /s B. 9m /s C. 4m /s D. 3m /s
1. 曲线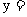
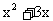 在
在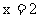 处的切线的斜率为 ( )
处的切线的斜率为 ( )
A. 7 B. 6 C. 5 D. 4
14. 解: (1) 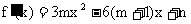 因为
因为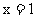 是函数
是函数 的一个极值点, 所以
的一个极值点, 所以
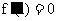 , 即
, 即 所以
所以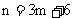
(2) 由(1)知, 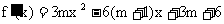
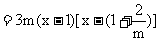
当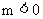 时, 有
时, 有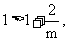 当x变化时,
当x变化时, 与
与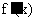 的变化如下表:
的变化如下表:

故有上表知, 当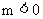 时,
时,  在
在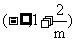 单调递减, 在
单调递减, 在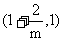 单调递增, 在
单调递增, 在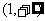
上单调递减.
(3) 由已知得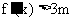 , 即
, 即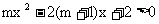
又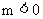 所以
所以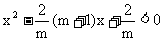 , 即
, 即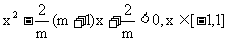 ……①
……①
设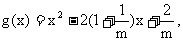 其函数开口向上, 由题意知①式恒成立,
其函数开口向上, 由题意知①式恒成立,
所以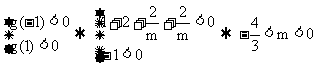 , 即m的取值范围为
, 即m的取值范围为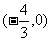 .
.
13. 解: (1) 由 的图象经过P
的图象经过P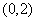 ,知
,知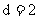 , 所以
, 所以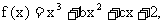
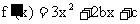 .即
.即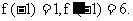
由在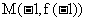 处的切线方程是
处的切线方程是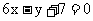 , 知
, 知
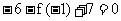 ,
,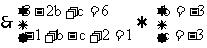
故所求的解析式是 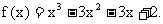
(2) 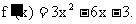 令
令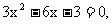 即
即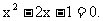
解得 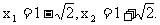 当
当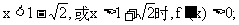
当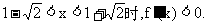
故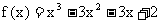 在
在 内是增函数, 在
内是增函数, 在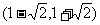 内是减函数,
内是减函数,
在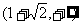 内是增函数.
内是增函数.
12. 解: 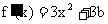 , 设
, 设 的极值点为(
的极值点为(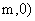 , 则
, 则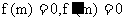 所以
所以
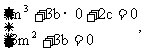 所以
所以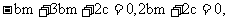 所以
所以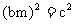 ,
,
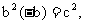 所以
所以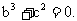
11. 解: (1) 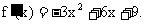 令
令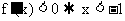 或
或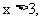
所以函数 的单调递减区间为
的单调递减区间为 ,
,  .
.
(2) 因为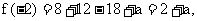

所以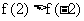 . 因为在
. 因为在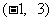 上
上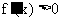 , 所以
, 所以 在
在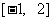 上单调递增, 又由于
上单调递增, 又由于
 在
在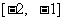 上单调递减, 因此
上单调递减, 因此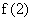 和
和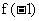 分别是
分别是 在区间
在区间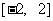 上的最大值和
上的最大值和
最小值, 于是有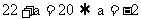 . 故
. 故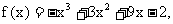
因此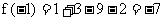 , 即函数
, 即函数 在区间
在区间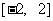 上的最小值为
上的最小值为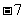 .
.
9. (提示: 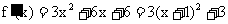 , 当
, 当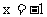 时,
时,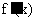 的最小值为
的最小值为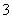 ,
,
所以当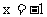 时,
时, 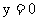 所求切线过点
所求切线过点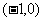 且斜率为3, 所以切线方程为
且斜率为3, 所以切线方程为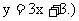
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com