
13.(2007届岳阳市一中高三数学能力题训练汇编)已知点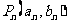 都在直线
都在直线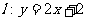 上,
上,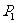 为直线
为直线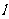 与
与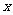 轴的交点,数列
轴的交点,数列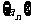 成等差数列,公差为1. (
成等差数列,公差为1. (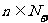 )
)
(1)求数列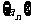 ,
,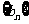 的通项公式;
的通项公式;
(2)若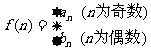 , 问是否存在
, 问是否存在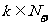 ,使得
,使得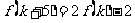 成立;若存在,求出
成立;若存在,求出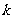 的值,若不存在,说明理由.
的值,若不存在,说明理由.
(3)求证: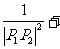
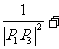 ……
+
……
+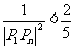 (
(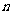
 2,
2,
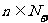 )
)
解 (1) 
(2)

假设存在符合条件的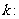
(ⅰ)若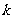 为偶数,则
为偶数,则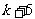 为奇数,有
为奇数,有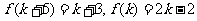
如果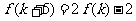 ,则
,则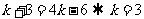 与
与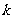 为偶数矛盾.不符舍去;
为偶数矛盾.不符舍去;
(ⅱ)
若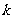 为奇数,则
为奇数,则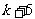 为偶数,有
为偶数,有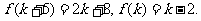
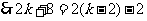 这样的
这样的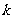 也不存在.
也不存在.
综上所述:不存在符合条件的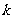 .
.
(3)
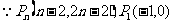
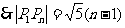
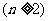
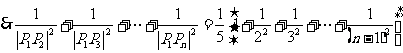
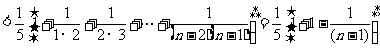
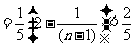
12.(武汉市2008届高中毕业生二月调研测试文科数学试题)设数列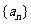 的前n项和
的前n项和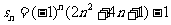 ,
,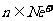 。
。
(1)求数列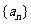 的通项公式
的通项公式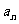 ;(2)记
;(2)记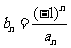 ,求数列
,求数列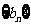 前n项和
前n项和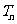
解:(1)数列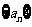 的前n项之和
的前n项之和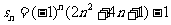
在n=1时,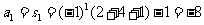
在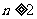 时,
时,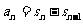
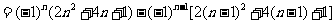
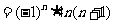
而n=1时,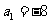 满足
满足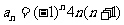
故所求数列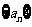 通项
通项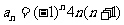 ………………………………(7分)
………………………………(7分)
(2)∵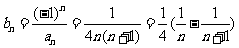
因此数列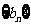 的前n项和
的前n项和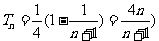 ………………………(12分)
………………………(12分)
11.(山东省潍坊市2007-2008学年度高三第一学期期末考试)已知数列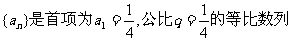 ,设
,设
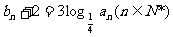 ,数列
,数列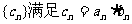 。
。
(1)求证: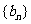 是等差数列;
是等差数列;
(2)求数列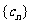 的前n项和Sn;
的前n项和Sn;
(3)若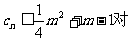 一切正整数n恒成立,求实数m的取值范围。
一切正整数n恒成立,求实数m的取值范围。
解:(1)由题意知,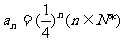 ……………………1分
……………………1分
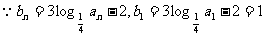
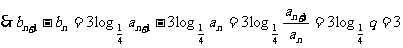
∴数列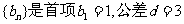 的等差数列……………………4分
的等差数列……………………4分
(2)由(1)知,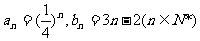
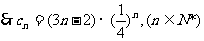 …………………………5分
…………………………5分

于是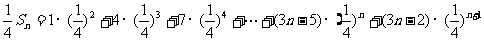
两式相减得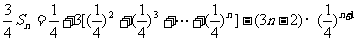
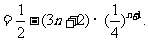
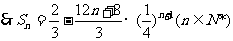 ……………………8分
……………………8分
(3)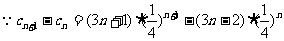
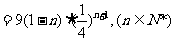
∴当n=1时,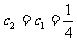
当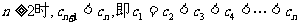
∴当n=1时,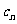 取最大值是
取最大值是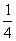
又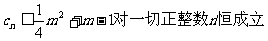
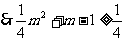
即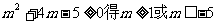 ……………………12分
……………………12分
10..(2008江苏省阜中2008届高三第三次调研考试试题)设集合W是满足下列两个条件的无穷数列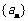 的集合:①
的集合:①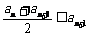 ; ②
; ②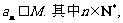 M是与n无关的常数.
M是与n无关的常数.
(1)若{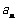 }是等差数列,
}是等差数列,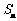 是其前n项的和,
是其前n项的和,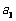 =4,
=4,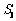 =18,试探究
=18,试探究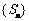 与集合W之间的关系;
与集合W之间的关系;
(2)设数{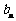 }的通项为
}的通项为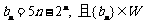 ,求M的取值范围;(4分)
,求M的取值范围;(4分)
解 (1)设等差数列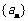 的公差是d ,则a1+2d=4,3a1+3d=18,解得a1=8,d =-2,
的公差是d ,则a1+2d=4,3a1+3d=18,解得a1=8,d =-2,
所以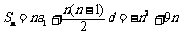 ,(2分),
,(2分),
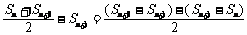
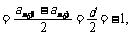
得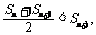 适合条件①. (4分);
适合条件①. (4分);
又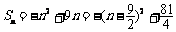 ,
,
所以当n = 4或5时,Sn取得最大值20,即Sn ≤ 20,适合条件②, (3分),
综上,{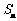 }
}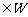 . (1分)
. (1分)
(2)因为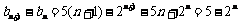 ,(2分),
,(2分),
所以当n≥3时,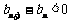 ,此时数列{bn}单调递减;(1分)
,此时数列{bn}单调递减;(1分)
当n = 1,2时,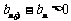 ,即b1<b2<b3,
,即b1<b2<b3,
因此数列{bn}中的最大项是b3=7,所以M≥7.(3分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com