
3、读书贵在生疑,重在解疑。第一段只有区区五个分句,语言简练,但字里行间隐藏许多内容,引导学生讨论。教师补充史料助读。
提示:“无礼于晋”指的是公元前637年晋公子重耳出亡途中路过郑国,郑文公不礼之事。“贰于楚也” 指的是公元前632年城濮之战前,郑文公背晋助楚,怂恿楚成王出兵作战,楚败,郑文公又与晋侯结盟之事。
一个弱小的郑国,同时受到两个强国的进攻,大军压境,国都被围,气氛十分紧张。“以其无礼于晋,且贰于楚也”,说明这次围郑主要是晋国为了报复,与秦国并没有多大的厉害关系,为下文烛之武退秦军埋下伏笔;“晋军函陵,秦军汜南”可见两国军队并没有驻扎在一起,也就为烛之武的分化瓦解工作提供了可能。“晋军”“汜南”均属郑国领土,分别为晋秦所占,一是说明晋秦联军来势凶猛,势不可挡;二是暗示郑国有机可乘。
开篇寥寥数语,既点出了战争爆发的原因,敌我双方力量的对比又为下文烛之武退秦军埋下伏笔,可见笔墨之经济。
㈡赏析第二段
2、学生结合课文注释理解文句并快速背诵。教师提示“以其无礼于晋,且贰于楚也”的句式特点并要求学生翻译。
㈠赏析第一段
1、诵读指导:“以其无礼于晋,且贰于楚也”是本段关键一句,语速要较慢,尤其是“且”处应稍作停顿,“也”字要拖长声音。此句读完,稍作停顿,再起后句“晋/军函陵,秦/军汜南”。“晋”“秦”之后要略作停顿。因为“军”在此名词活用为动词,当“驻扎”讲。
3、学生自由朗读后复述故事情节,教师引导学生概括情节并板书。
第一段:秦晋围郑
第二段:临危受命
第三段:说秦退军
第四段:晋侯撤兵
2、教师正音并提示文言异读现象(古音异读、通假异读、破读)
氾(fàn)南 佚(yì) 之狐 夜 缒(zhuì) 阙(jué) 秦 朝(zhāo)济 逢(páng)孙
戍(shù)之 失其所与(yǔ)) 夫(fú)人之力
共(供)(gōng)其乏困 不知(智)(zhì)
1、录音范读(最好教师范读),学生标注重点字词读音。
2、复习《左传》常识,教师补充。
《左传》相传为鲁国的史官左丘明所作,是我国第一部详细完整的编年体历史著作,为“十三经”之一。因与《公羊传》《谷梁传》均为解说《春秋》而作,故并称“春秋三传”。《左传》又名《左氏春秋》、《春秋左氏传》。
《左传》以《春秋》的记事为纲,以时间先后为序,详细地记述了春秋时期各国内政外交等大小事实。 起于鲁隐公元年,终于鲁哀公二十七年,记事比《春秋》详细而具体,保存了大量古代史料。有关春秋时期各诸候国间的政治、军事,外交以及经济、文化等方面的重大史实都有载述,具体面完整地显示了时代概貌。
《左传》善于描写战争和记述行人辞令,叙事委婉详尽,情节富于故事性和戏剧性,描写人物婉而有致,人物形象性格鲜明、栩栩如生,常常是寥寥几句,就能使读者如见其人,如闻其声,显示了作者高超的艺术表现能力。
1、由初中学习过的《曹刿论战》导入,学生回顾,教师补充,并齐诵《曹刿论战》的精彩语句,如“一鼓作气,再而衰,三而竭,彼竭我盈,故克之。”
3.反冲问题:在某些情况下,原来系统内物体具有相同的速度,发生相互作用后各部分的末速度不再相同而分开。这类问题相互作用过程中系统的动能增大,有其它能向动能转化。可以把这类问题统称为反冲。
例题分析
例1:质量为M的楔形物块上有圆弧轨道,静止在水平面上。质量为m
的小球以速度v1向物块运动。不计一切摩擦,圆弧小于90°且足够长。
求小球能上升到的最大高度H 和物块的最终速度v。
解:系统水平方向动量守恒,全过程机械能也守恒。
在小球上升过程中,由水平方向系统动量守恒得: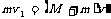
由系统机械能守恒得: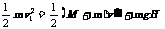 解得
解得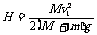
全过程系统水平动量守恒,机械能守恒,得
本题和上面分析的弹性碰撞基本相同,唯一的不同点仅在于重力势能代替了弹性势能。
例2:动量分别为5kgžm/s和6kgžm/s的小球A、B沿光滑平面上的同一条直线同向运动,A追上B并发生碰撞后。若已知碰撞后A的动量减小了2kgžm/s,而方向不变,那么A、B质量之比的可能范围是什么?
 解:A能追上B,说明碰前vA>vB,∴
解:A能追上B,说明碰前vA>vB,∴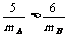 ;碰后A的速度不大于B的速度,
;碰后A的速度不大于B的速度, 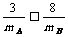 ;又因为碰撞过程系统动能不会增加,
;又因为碰撞过程系统动能不会增加,
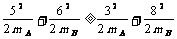 ,由以上不等式组解得:
,由以上不等式组解得: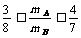
此类碰撞问题要考虑三个因素:①碰撞中系统动量守恒;②碰撞过程中系统动能不增加;③碰前、碰后两个物体的位置关系(不穿越)和速度大小应保证其顺序合理。
例3:设质量为m的子弹以初速度v0射向静止在光滑水平面上的质量为M的木块,并留在木块中不再射出,子弹钻入木块深度为d。求木块对子弹的平均阻力的大小和该过程中木块前进的距离。
解:子弹和木块最后共同运动,相当于完全非弹性碰撞。从动量的角度看,子弹射入木块过程中系统动量守恒:
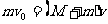
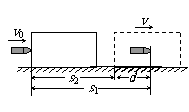
从能量的角度看,该过程系统损失的动能全部转化为系统的内能。设平均阻力大小为f,设子弹、木块的位移大小分别为s1、s2,如图所示,显然有s1-s2=d
对子弹用动能定理: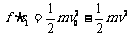 ……①
……①
对木块用动能定理: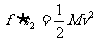 ……②
……②
①、②相减得: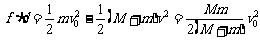 ……③
……③
这个式子的物理意义是:fžd恰好等于系统动能的损失;根据能量守恒定律,系统动能的损失应该等于系统内能的增加;可见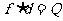 ,即两物体由于相对运动而摩擦产生的热(机械能转化为内能),等于摩擦力大小与两物体相对滑动的路程的乘积(由于摩擦力是耗散力,摩擦生热跟路径有关,所以这里应该用路程,而不是用位移)。
,即两物体由于相对运动而摩擦产生的热(机械能转化为内能),等于摩擦力大小与两物体相对滑动的路程的乘积(由于摩擦力是耗散力,摩擦生热跟路径有关,所以这里应该用路程,而不是用位移)。
由上式不难求得平均阻力的大小: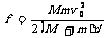
至于木块前进的距离s2,可以由以上②、③相比得出:
从牛顿运动定律和运动学公式出发,也可以得出同样的结论。由于子弹和木块都在恒力作用下做匀变速运动,位移与平均速度成正比:
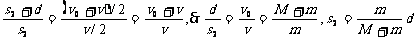
一般情况下 ,所以s2<<d。这说明,在子弹射入木块过程中,木块的位移很小,可以忽略不计。这就为分阶段处理问题提供了依据。象这种运动物体与静止物体相互作用,动量守恒,最后共同运动的类型,全过程动能的损失量可用公式:
,所以s2<<d。这说明,在子弹射入木块过程中,木块的位移很小,可以忽略不计。这就为分阶段处理问题提供了依据。象这种运动物体与静止物体相互作用,动量守恒,最后共同运动的类型,全过程动能的损失量可用公式: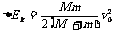 …④
…④
当子弹速度很大时,可能射穿木块,这时末状态子弹和木块的速度大小不再相等,但穿透过程中系统动量仍然守恒,系统动能损失仍然是ΔEK= f žd(这里的d为木块的厚度),但由于末状态子弹和木块速度不相等,所以不能再用④式计算ΔEK的大小。
做这类题目时一定要画好示意图,把各种数量关系和速度符号标在图上,以免列方程时带错数据。
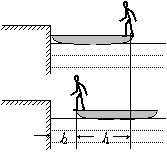 例4:质量为m的人站在质量为M,长为L的静止小船的右端,小船的左端靠在岸边。当他向左走到船的左端时,船左端离岸多远?
例4:质量为m的人站在质量为M,长为L的静止小船的右端,小船的左端靠在岸边。当他向左走到船的左端时,船左端离岸多远?
解:先画出示意图。人、船系统动量守恒,总动量始终为零,所以人、船动量大小始终相等。从图中可以看出,人、船的位移大小之和等于L。设人、船位移大小分别为l1、l2,则:mv1=Mv2,两边同乘时间t,ml1=Ml2,而l1+l2=L,∴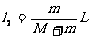
应该注意到:此结论与人在船上行走的速度大小无关。不论是匀速行走还是变速行走,甚至往返行走,只要人最终到达船的左端,那么结论都是相同的。
做这类题目,首先要画好示意图,要特别注意两个物体相对于地面的移动方向和两个物体位移大小之间的关系。
以上所列举的人、船模型的前提是系统初动量为零。如果发生相互作用前系统就具有一定的动量,那就不能再用m1v1=m2v2这种形式列方程,而要利用(m1+m2)v0= m1v1+ m2v2列式。
例5:总质量为M的火箭模型 从飞机上释放时的速度为v0,速度方向水平。火箭向后以相对于地面的速率u喷出质量为m的燃气后,火箭本身的速度变为多大?
解:火箭喷出燃气前后系统动量守恒。喷出燃气后火箭剩余质量变为M-m,以v0方向为正方向,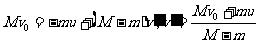
2.子弹打木块类问题:子弹打木块实际上是一种完全非弹性碰撞。作为一个典型,它的特点是:子弹以水平速度射向原来静止的木块,并留在木块中跟木块共同运动。下面从动量、能量和牛顿运动定律等多个角度来分析这一过程。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com