1. 三点确定一个平面的条件是___________；

共点的四条直线最多可以确定_______平面；

互不相交的三条直线可以确定_______平面.

(二)空间两条直线

1．空间两直线的位置关系有：

(1)相交；　 (2)平行；

(3)异面.定义--

2 公理4 ：平行于同一条直线的两条直线互相平行.

3 等角定理：一个角的两边和另一个角的两边分别平行且方向相同，则这两个角相等.

推论:两条相交直线和另两条相交直线分别平行,则这两条直线所成的角相等.

4 空间两条异面直线:不同在任何全个平面内.

判定定理：过平面内一点与平面外一点的直线，和这个平面内不经过此点的直线是异面直线.

5．异面直线所成的角的求法：

找(或)作出过一条直线上一点,于另一直线平直线;或过空间一点与两条直线平行的直线,转化为平面内的角,再用平面几何的方法去求;也可用向量法.

注意:两条直线所成的角的范围: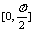. 两条异面直线所成的角的范围:.

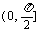6 两条异面直线的公垂线、距离

和两条异面直线都垂直且相交的直线，我们称之为异面直线的公垂线.

理解：和异面直线都垂直的直线有无数条，公垂线只有一条.

两条异面直线的公垂线在这两条异面直线间的线段(公垂线段)的长度，叫做两条异面直线间的距离．

　 计算方法：①几何法；②向量法

(一)平面的概念和性质

1．平面的概念：平面是没有厚薄的，可以无限延伸.

2．空间点、线、面的位置关系及表示：要正确运用下列符号：

点A,B,C,…;直线 a,b,c,…;平面α,β,γ…

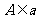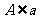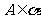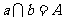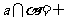,,,,,,a∥b,a⊥b,a∥α,a⊥β, α⊥β, α//β, α⊥β, α∩β=a

3．平面的基本性质

公理1.线的在平面内.

用途：判定直线在平面内，验证是否平面．

公理2两个平面的交线.　　　

用途：①确定两相交平面的交线；②判定点在直线上.

公理3及其三个推论: 确定平面的条件.

注意“确定”即“有且只有一个”的含义．

4．所有点都在一个平面内的图形称为平面图形，否则称为空间图形.

3．能进行简单的文字、符号、图形三者之间的转化.

2．掌握空间两直线的位置关系，理解异面直线的定义，能证明和判断两条直线是异面直线.能用图形表示两条直线的位置关系，会解决与位置关系有关的问题.

1．掌握平面的基本性质，会运用这些性质解决有关共面、共线、共点、交线等问题.

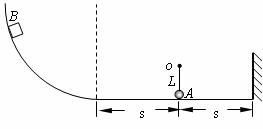
19．(10分)如图所示，一长度L=0.2m的轻质细绳一端系一质量m=0.5kg的小球A，另一端挂在光滑水平轴o上，小球A和水平面接触但无相互作用，在球的两侧等距离s=1m处分别固定一光滑大圆弧面和一挡板。现有一小滑块B，质量也为m，从圆弧面上滑下，与小球A碰撞时交换速度，与挡板碰撞时不损失机械能。若滑块B从圆弧面某一高度h处由静止滑下与小球A第一次碰撞后，使小球A恰好在竖直面内做圆周运动。已知滑块与水平面间的动摩擦因数μ=0.25(不计空气阻力，将滑块和小球视为质点，g=10m／s²)。求

　　 ⑴ A、B第一次碰撞后的瞬间绳子的拉力；

　　 ⑵ 高度h；

　　 ⑶ 若滑块B从圆弧面上高度H=6.25m处由静止滑下，与小球A碰撞后，小球A所能完成的完整圆周运动的次数。

18．(9分)如图所示，在水平面上有2个质量均为m=1kg的小木箱排成一条直线，小木箱之间的距离L=1m。现用水平恒力F推第一个小木箱使之滑动，然后与另一小木箱相碰。碰撞后两木箱粘在一起，且恰好做匀速运动。整个过程中恒力不变，已知小木箱与地面之间的动摩擦因数均为μ=0.1，重力加速度g=10m/s²，设碰撞时间极短，求：

⑴水平推力F；

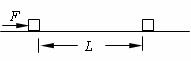⑵两木箱匀速运动的速度；

⑶在碰撞过程中损失的机械能。

17．(8分)“黑洞”是质量足够大并足够致密的恒星，它有强大的引力场，以至于连光线都不能逃逸，所以我们无法看见它，但我们可以根据它周围星体的运动来判断它的存在。在下列两种情况下求“黑洞”的质量M(已知万有引力常量为G)

⑴若已知某一恒星围绕该“黑洞”做匀速圆周运动的半径为R、周期为T；

⑵若已知该黑洞在距离“黑洞”中心H处产生的重力加速度为。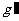

16．(7分)一列沿着x轴正方向传播的简谐横波，某时刻的波形如图所示。其周期为0.4s。

⑴ 指出该时刻P点的振动方向;

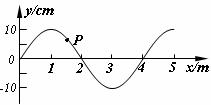⑵ 求该波的波长;

⑶ 求该波的波速。