
2.(2008惠州调研二理)方程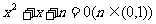 有实根的概率为(
).
有实根的概率为(
).
A、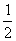 B、
B、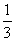 C、
C、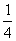 D、
D、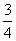
1.(2008辽宁文、理) 4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为( )
A.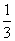 B.
B.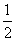 C.
C.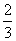 D.
D.
5.不确定关系的应用
(1)估算氢原子可能具有的最低能量
电子束缚在半径为r的球内,所以
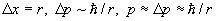
当不计核的运动,氢原子的能量就是电子的能量:
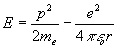
用不确定关系代入上式得:
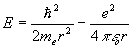
基态能应满足
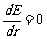 得
得
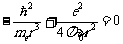
由此得出基态氢原子半径
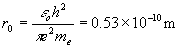
基态氢原子的能量
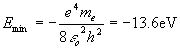
与波尔理论结果一致。
(2) 解释谱线的自然宽度
原子中某激发态的平均寿命为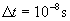
由普朗克能量子假说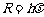 及
及
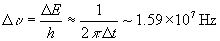
这就是谱线的自然宽度。

[例1]已知一个光子沿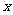 方向传播,其波长
方向传播,其波长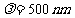 ,对波长的测量是相当准确的,
,对波长的测量是相当准确的,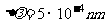 ,求该光子
,求该光子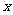 坐标的不确定度;
坐标的不确定度;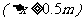
[例2]质量为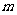 的粒子位置的不确定量等于粒子的德布罗意波长
的粒子位置的不确定量等于粒子的德布罗意波长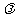 ,求
,求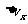 的最小值.
的最小值.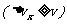
[例3]氢原子中基态电子的速度大约是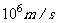 ,电子位置的不确定度可按原子大小估算
,电子位置的不确定度可按原子大小估算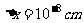 ,求电子速度的不确定度.
,求电子速度的不确定度.
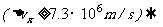 轨道概念在量子力学中无意义!
轨道概念在量子力学中无意义!
4.其它表示:
能量、时间:
角动量、角位移:
3.讨论
(1)不确定关系式表示电子的坐标及相应的动量不能同时准确测量
(2)不确定关系取决于电子本身的固有特性-波粒二象性,即精度、方法等都无济于事
(3)对宏观物体讲不受此限制
2.测不准关系的推证(1927年,海森堡)
微观粒子的位置和动量具有不确定性,这可用电子单缝衍射实验说明,并验证不确定关系.
如下图所示,设有一束电子,以速度v沿y轴射向AB屏上的单缝,缝宽为d,在屏幕CD上得到衍射图样,衍射的第一极小角为q1 ,则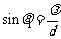
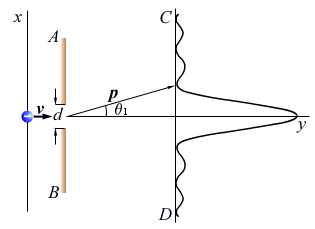
电子位置在x方向上的不确定量为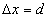 ,由于衍射的缘故,电子在x方向上动量分量px具有各种不同的量值.如果只考虑衍射主极大区域,则x方向动量不确定度为
,由于衍射的缘故,电子在x方向上动量分量px具有各种不同的量值.如果只考虑衍射主极大区域,则x方向动量不确定度为
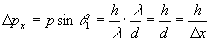
即
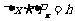
如果考虑高次衍射条纹,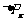 还要大些,
还要大些,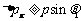 ,因此一般地有
,因此一般地有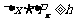
这就是海森堡分析得到的不确定关系.
不确定度关系不是仪器的误差,或人为测量误差造成的,而是波粒二象性的必然结果.我们只能说粒子位置不确定性越大(d越宽),粒子的动量就越确定.能级的寿命越长,能级的宽度(不确定度)就越小,辐射产生的谱线宽度就越小,单色性就越好,反之亦然.
1.描述物体的运动状态
(1)宏观: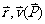 ,两者可同时准确测量;
,两者可同时准确测量;
(2)微观粒子: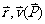 不能同时准确测量,原因是微观粒子具有波、粒二象性,有测不准关系:
不能同时准确测量,原因是微观粒子具有波、粒二象性,有测不准关系: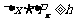
即:粒子有某方向的坐标测不准量与该方向上的动量分量的测不准量的积,必不小于普朗克常数;位置测得越准,动量测得越不准!
现代量子力学证明: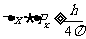
3.德布罗意假设的实验验证
德布罗意关于物质波的假设在微观粒子的衍射实验中得到了验证。其中最有代表性的是电子散射实验、透射实验和双缝干涉实验。这些实验有力地证明了德布罗意物质波假说的正确性。
实物粒子的衍射效应在近代科技中有广泛的应用,例如中子衍射技术,已成为研究固体微观结构的最有效的手段之一。
光学仪器的分辨率与波长成正比,而电子的德布罗意波长比光波长短很多,例如在10万伏的加速电压下,电子的波长只有0.004 m,比可见光短10万倍左右,因而利用电子波代替光波制成电子显微镜就可以有极高的分辨本领。现代的电子显微镜不仅可以直接看到如蛋白质一类的大分子,而且能分辨单个原子的尺寸,为研究物质结构提供了有力的工具。
(1) 电子散射实验
电子散射实验的典型代表是戴维孙-革末实验。1927年戴维孙和革末用电子束垂直投射到镍单晶,电子束被散射。电子经晶格散射后在某一特定方向衍射极大,这一结果与X射线散射相似,其强度分布可用德布罗意关系和衍射理论给以解释,从而验证了物质波的存在。
衍射加强时的电子德布罗意波长应满足布拉格公式
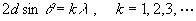
式中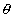 是入射电子束对晶面的掠射角,d是晶面间距。晶面间距d与镍原子的间隔l的关系是
是入射电子束对晶面的掠射角,d是晶面间距。晶面间距d与镍原子的间隔l的关系是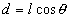 ,考虑第一级衍射极大,有
,考虑第一级衍射极大,有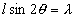
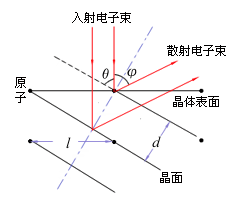
由图知电子相对于入射方向的散射角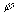 与掠射角
与掠射角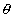 之间有关系
之间有关系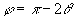 ,因此上式可写成
,因此上式可写成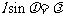
当加速电压U=54伏,加速电子的能量: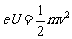
电子的德布罗意波长: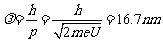
镍的原子间隔是21.5nm,由此求出衍射第一极大的散射角度: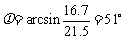
实验测量出的值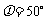 ,是理论值比实验值稍大的原因是电子受正离子的吸引,在晶体中的波长比在真空中稍小(动量稍大)。经修正后,理论值与实验结果完全符合。
,是理论值比实验值稍大的原因是电子受正离子的吸引,在晶体中的波长比在真空中稍小(动量稍大)。经修正后,理论值与实验结果完全符合。
(2) 电子透射实验
电子穿过晶体薄片后产生的衍射,与X射线通过晶体的衍射极其类似。汤姆逊实验证明了电子在穿过金属片后也象X射线一样产生衍射现象。下图是电子射线通过多晶时的衍射图样。

戴维逊和汤姆逊因验证电子的波动性分享1937年的物理学诺贝尔奖金。
(3) 电子双缝干涉实验
1960年,约恩孙直接做了电子双缝干涉实验,从屏上摄得了类似杨氏双缝干涉图样的照片。干涉图样如下图所示。

在电子波动性获得证实以后,在其它一些实验中也观察到中性粒子如分子、原子和中子等微观粒子,也具有波动性,1988年蔡林格等做了中子的双缝实验。德布罗意公式也同样正确,德布罗意公式成了波粒二象性的统一性的基本公式,德布罗意由于发现电子的波动性,荣获1929年诺贝尔物理学奖。
[例1]求波长都等于0.2nm的光子与电子的总能量和动量
[例2]电子通过单缝的实验中,加速电压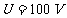 ,垂直穿过
,垂直穿过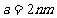 的单缝,求:
的单缝,求:
① 加速后的速率;
② 电子相应的波长;
③
中央明纹的半角宽度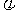
解:① 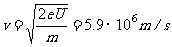 ②
② 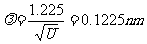
③ 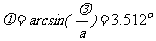
第四讲 测不准关系
2.德布罗意假设
(1)假设:质量为m的粒子,以速度v运动时,不但具有粒子的性质,也具有波动的性质;
粒子性:可用E、P描述
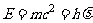 ,
, 
波动性:可用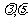 描述
描述
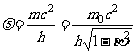 ,
,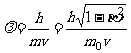 -------德布罗意公式
-------德布罗意公式
(2)电子的德布罗意波长
加速电势差为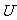 ,则:
,则: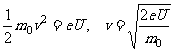
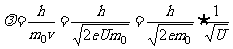
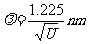
如: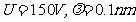 (与
(与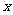 射线的波长相当)
射线的波长相当)

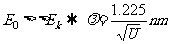
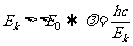
1.光的波粒二象性
波动性:干涉、衍射、偏振
粒子性:热辐射,光电效应,散射等
同时具有,不同时显现
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com