
4.给出下列命题:①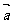 ·
·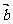 =0,则
=0,则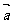 =0或
=0或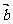 =0. ②若
=0. ②若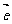 为单位向量且
为单位向量且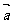 //
//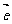 ,则
,则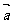 =|
=|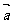 |·
|·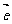 .
.
③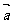 ·
·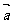 ·
·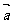 =|
=|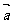 |3. ④若
|3. ④若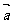 与
与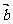 共线,
共线,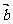 与
与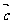 共线,则
共线,则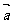 与
与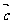 共线.其中正确的个数是 ( )
共线.其中正确的个数是 ( )
A.0 B.1 C.2 D.3
3.把直线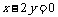 按向量
按向量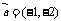 平移后,所得直线与圆
平移后,所得直线与圆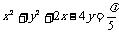 相
相
切,则实数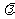 的值为 ( A )
的值为 ( A )
A.39 B.13 C.-21 D.-39
2.已知△ABC中,点D在BC边上,且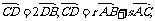 则
则 的值是( )
的值是( )
A.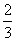 B.
B.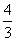 C.-3 D.0
C.-3 D.0
1.已知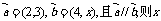 的值为 ( )
的值为 ( )
A.-6 B.6 C.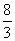 D.-
D.-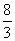
2.导数的几何意义.
1.曲线的切线及切线的斜率.
2.求曲线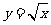 在点
在点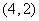 处的切线.
处的切线.
1.求曲线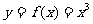 在点
在点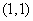 处的切线.
处的切线.
例1
(1)求曲线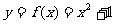 在点
在点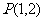 处的切线方程.
处的切线方程.
(2)求函数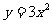 在点
在点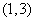 处的导数.
处的导数.
解: (1)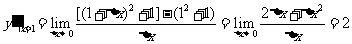
所以,所求切线的斜率为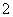
因此,所求的切线方程为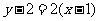 即
即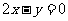
(2)因为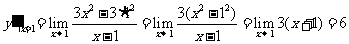
所以,所求切线的斜率为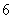 ,
,
因此,所求的切线方程为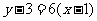 即
即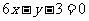
例2 如图3.1-3,它表示跳水运动中高度随时间变化的函数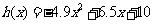 ,根据图像,请描述、比较曲线
,根据图像,请描述、比较曲线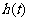 在
在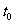 、
、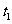 、
、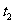 附近的变化情况.
附近的变化情况.
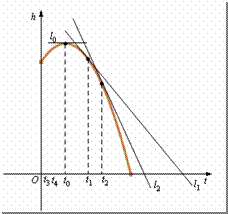 解: 我们用曲线
解: 我们用曲线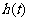 在
在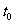 、
、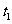 、
、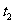 处的切线,
处的切线,
刻画曲线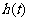 在上述三个时刻附近的变化情况.
在上述三个时刻附近的变化情况.
(1)
当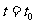 时,曲线
时,曲线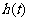 在
在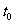 处的切线
处的切线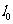 平行于
平行于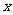 轴,
轴,
所以,在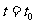 附近曲线比较平坦,几乎没有升降.
附近曲线比较平坦,几乎没有升降.
(2)当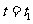 时,曲线
时,曲线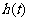 在
在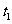 处的切线
处的切线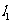 的斜率
的斜率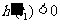 ,
,
所以,在 附近曲线下降,
附近曲线下降,
即函数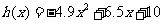 在
在 附近单调递减.
附近单调递减.
(3)当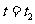 时,曲线
时,曲线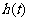 在
在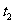 处的切线
处的切线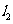 的斜率
的斜率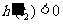 ,
,
所以,在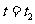 附近曲线下降,
附近曲线下降,
即函数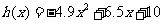 在
在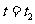 附近单调递减.
附近单调递减.
从图3.1-3可以看出,直线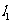 的倾斜程度小于直线
的倾斜程度小于直线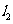 的倾斜程度,
的倾斜程度,
这说明曲线在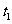 附近比在
附近比在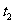 附近下降的缓慢.
附近下降的缓慢.
 例3 如图3.1-4,它表示人体血管中药物浓度
例3 如图3.1-4,它表示人体血管中药物浓度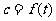 (单位:
(单位: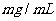 )随时间
)随时间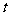 (单位:
(单位: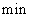 )变化的图象.根据图像,估计
)变化的图象.根据图像,估计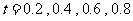 时,血管中药物浓度的瞬时变化率(精确到
时,血管中药物浓度的瞬时变化率(精确到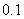 ).
).
解: 血管中某一时刻药物浓度的瞬时变化率,就是药物浓度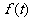 在此时刻的导数,
在此时刻的导数,
从图像上看,它表示曲线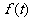 在此点处的切线的斜率.
在此点处的切线的斜率.
如图3.1-4,画出曲线上某点处的切线,利用网格估计这条切线的斜率,
可以得到此时刻药物浓度瞬时变化率的近似值.
作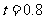 处的切线,并在切线上去两点,如
处的切线,并在切线上去两点,如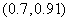 ,
,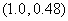 ,
,
则它的斜率为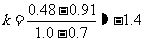 ,所以
,所以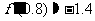
下表给出了药物浓度瞬时变化率的估计值:
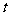 |
0.2 |
0.4 |
0.6 |
0.8 |
药物浓度瞬时变化率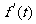 |
0.4 |
0 |
-0.7 |
-1.4 |
(四)函数 在点
在点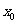 处的导数
处的导数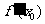 、导函数
、导函数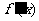 、导数之间的区别与联系
、导数之间的区别与联系
(1)函数在一点处的导数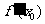 ,就是在该点的函数的改变量与自变量的改变量之比的极限,它是一个常数,不是变数.
,就是在该点的函数的改变量与自变量的改变量之比的极限,它是一个常数,不是变数.
(2)函数的导数,是指某一区间内任意点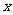 而言的,就是函数
而言的,就是函数 的导函数.
的导函数.
(3)函数 在点
在点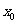 处的导数
处的导数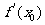 就是导函数
就是导函数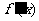 在
在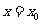 处的函数值,这也是求函数在点
处的函数值,这也是求函数在点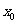 处的导数的方法之一.
处的导数的方法之一.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com