
14、(2009年烟台市)23.(本题满分10分)某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
解:(1)根据题意,得 ,
,
即 .······················································································ 2分
.······················································································ 2分
(2)由题意,得 .
.
整理,得 .················································································ 4分
.················································································ 4分
解这个方程,得 .·········································································· 5分
.·········································································· 5分
要使百姓得到实惠,取 .所以,每台冰箱应降价200元.································· 6分
.所以,每台冰箱应降价200元.································· 6分
(3)对于 ,
,
当 时,······················································································ 8分
时,······················································································ 8分
 .
.
所以,每台冰箱的售价降价150元时,商场的利润最大,最大利润是5000元. 10分
13、(2009年山西省太原市)28.(本小题满分9分) 、
、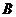 两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往
两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往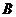 城,乙车驶往
城,乙车驶往 城,甲车在行驶过程中速度始终不变.甲车距
城,甲车在行驶过程中速度始终不变.甲车距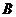 城高速公路入口处的距离
城高速公路入口处的距离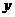 (千米)与行驶时间
(千米)与行驶时间 (时)之间的关系如图.
(时)之间的关系如图.
(1)求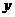 关于
关于 的表达式;
的表达式;
(2)已知乙车以60千米/时的速度匀速行驶,设行驶过程中,两车相距的路程为 (千米).请直接写出
(千米).请直接写出 关于
关于 的表达式;
的表达式;
 (3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为
(3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为 (千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度
(千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度 .在下图中画出乙车离开
.在下图中画出乙车离开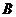 城高速公路入口处的距离
城高速公路入口处的距离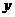 (千米)与行驶时间
(千米)与行驶时间 (时)之间的函数图象.
(时)之间的函数图象.
解:(1)方法一:由图知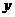 是
是 的一次函数,设
的一次函数,设 ········································ 1分
········································ 1分
 图象经过点(0,300),(2,120),∴
图象经过点(0,300),(2,120),∴ ··························· 2分
··························· 2分
解得 ························································································ 3分
························································································ 3分
∴ 即
即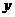 关于
关于 的表达式为
的表达式为 ····················· 4分
····················· 4分
方法二:由图知,当 时,
时, ;
; 时,
时,
所以,这条高速公路长为300千米.
甲车2小时的行程为300-120=180(千米).
∴甲车的行驶速度为180÷2=90(千米/时).··········································· 3分
∴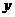 关于
关于 的表达式为
的表达式为 (
( ).······················ 4分
).······················ 4分
(2) ······················································································ 5分
······················································································ 5分
(3)在 中.当
中.当 时,
时,
即甲乙两车经过2小时相遇.············································································· 6分
 在
在 中,当
中,当 .所以,相遇后乙车到达终点所用的时间为
.所以,相遇后乙车到达终点所用的时间为 (小时).
(小时).
乙车与甲车相遇后的速度
 (千米/时).
(千米/时).
∴ (千米/时).··································· 7分
(千米/时).··································· 7分
乙车离开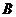 城高速公路入口处的距离
城高速公路入口处的距离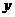 (千米)与行
(千米)与行
驶时间 (时)之间的函数图象如图所示.·············· 9分
(时)之间的函数图象如图所示.·············· 9分
12、(2009年山西省)(24.(本题8分)某批发市场批发甲、乙两种水果,根据以往经验和市场行情,预计夏季某一段时间内,甲种水果的销售利润 (万元)与进货量
(万元)与进货量 (吨)近似满足函数关系
(吨)近似满足函数关系 ;乙种水果的销售利润
;乙种水果的销售利润 (万元)与进货量
(万元)与进货量 (吨)近似满足函数关系
(吨)近似满足函数关系 (其中
(其中 为常数),且进货量
为常数),且进货量 为1吨时,销售利润
为1吨时,销售利润 为1.4万元;进货量
为1.4万元;进货量 为2吨时,销售利润
为2吨时,销售利润 为2.6万元.
为2.6万元.
(1)求 (万元)与
(万元)与 (吨)之间的函数关系式.
(吨)之间的函数关系式.
(2)如果市场准备进甲、乙两种水果共10吨,设乙种水果的进货量为 吨,请你写出这两种水果所获得的销售利润之和
吨,请你写出这两种水果所获得的销售利润之和 (万元)与
(万元)与 (吨)之间的函数关系式.并求出这两种水果各进多少吨时获得的销售利润之和最大,最大利润是多少?
(吨)之间的函数关系式.并求出这两种水果各进多少吨时获得的销售利润之和最大,最大利润是多少?
解:(1)由题意,得: 解得
解得 ······················································· (2分)
······················································· (2分)
∴ ····················································································· (3分)
····················································································· (3分)
(2)
∴ ··················································································· (5分)
··················································································· (5分)
 ∴
∴ 时,
时, 有最大值为6.6.
····························· (7分)
有最大值为6.6.
····························· (7分)
∴ (吨).
(吨).
答:甲、乙两种水果的进货量分别为4吨和6吨时,获得的销售利润之和最大,最大利润是6.6万元. (8分)
11、(重庆市2009年)25.某电视机生产厂家去年销往农村的某品牌电视机每台的售价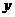 (元)与月份
(元)与月份 之间满足函数关系
之间满足函数关系 ,去年的月销售量
,去年的月销售量 (万台)与月份
(万台)与月份 之间成一次函数关系,其中两个月的销售情况如下表:
之间成一次函数关系,其中两个月的销售情况如下表:
|
月份 |
1月 |
5月 |
|
销售量 |
3.9万台 |
4.3万台 |
(1)求该品牌电视机在去年哪个月销往农村的销售金额最大?最大是多少?
(2)由于受国际金融危机的影响,今年1、2月份该品牌电视机销往农村的售价都比去年12月份下降了 ,且每月的销售量都比去年12月份下降了
,且每月的销售量都比去年12月份下降了 。国家实施“家电下乡”政策,即对农村家庭购买新的家电产品,国家按该产品售价的13%给予财政补贴。受此政策的影响,今年3月份至5月份,该厂家销往农村的这种电视机在保持今年2月份的售价不变的情况下,平均每月的销售量比今年2月份增加了1.5万台。若今年3至5月份国家对这种电视机的销售共给予财政补贴936万元,求
。国家实施“家电下乡”政策,即对农村家庭购买新的家电产品,国家按该产品售价的13%给予财政补贴。受此政策的影响,今年3月份至5月份,该厂家销往农村的这种电视机在保持今年2月份的售价不变的情况下,平均每月的销售量比今年2月份增加了1.5万台。若今年3至5月份国家对这种电视机的销售共给予财政补贴936万元,求 的值(保留一位小数)
的值(保留一位小数)
解: (1)p=0.1x+3.8
月销售金额w=py=-5(x-7) +10125
+10125
故7月销售金额最大,最大值是10125万元
(2)列方程得
2000(1-m%)[5(1-1.5 m%)+1.5]×3×13%=936
化简得 3m -560m+21200=0 解得 m
-560m+21200=0 解得 m =
= m
m =
=
因为m >1舍去,所以m=52.78≈52.8
>1舍去,所以m=52.78≈52.8
(参考数据: ,
, ,
, ,
, )
)
10、(重庆市2009年)25.某商场在销售旺季临近时 ,某品牌的童装销售价格呈上升趋势,假如这种童装开始时的售价为每件20元,并且每周(7天)涨价2元,从第6周开始,保持每件30元的稳定价格销售,直到11周结束,该童装不再销售。
(1)请建立销售价格y(元)与周次x之间的函数关系;
(2)若该品牌童装于进货当周售完,且这种童装每件进价z(元)与周次x之间的关系为 , 1≤ x ≤11,且x为整数,那么该品牌童装在第几周售出后,每件获得利润最大?并求最大利润为多少?
, 1≤ x ≤11,且x为整数,那么该品牌童装在第几周售出后,每件获得利润最大?并求最大利润为多少?
9、(内江市二○○九年)6.(10分)我市部分地区近年出现持续干旱现象,为确保生产生活用水,某村决定由村里提供一点,村民捐一点的办法筹集资金维护和新建一批储水池.该村共有243户村民,准备维护和新建的储水池共有20个,费用和可供使用的户数及用地情况如下表:
|
储水池 |
费用(万元/个) |
可供使用的户数(户/个) |
占地面积(m2/个) |
|
新建 |
4 |
5 |
4 |
|
维护 |
3 |
18 |
6 |
已知可支配使用土地面积为106m2,若新建储水池 个,新建和维护的总费用为
个,新建和维护的总费用为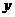 万元.
万元.
(1)求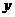 与
与 之间的函数关系;
之间的函数关系;
(2)满足要求的方案各有几种;
(3)若平均每户捐2000元时,村里出资最多和最少分别是多少?
8、(成都市二0 0九年)(共8分)26.某大学毕业生响应国家“自主创业”的号召,投资开办了一个装饰品商店.该店采购进一种今年新上市的饰品进行了30天的试销售,购进价格为20元/件.销售结束后,得知日销售量P(件)与销售时间x(天)之间有如下关系:P=-2x+80(1≤x≤30,且x为整数);又知前20天的销售价格 (元/件)与销售时间x(天)之间有如下关系:
(元/件)与销售时间x(天)之间有如下关系: (1≤x≤20,且x为整数),后10天的销售价格
(1≤x≤20,且x为整数),后10天的销售价格 (元/件)与销售时间x(天)之间有如下关系:
(元/件)与销售时间x(天)之间有如下关系: =45(21≤x≤30,且x为整数).
=45(21≤x≤30,且x为整数).
(1)试写出该商店前20天的日销售利润 (元)和后l0天的日销售利润
(元)和后l0天的日销售利润 (元)分别与销售时间x(天)之间的函数关系式;
(元)分别与销售时间x(天)之间的函数关系式;
(2)请问在这30天的试销售中,哪一天的日销售利润最大?并求出这个最大利润.
注:销售利润=销售收入一购进成本.
7、(2009年宜宾市)23.(本题满分8分) 从2008年12月1日起,国家开始实施家电下乡计划,国家将按照农民购买家电金额的13%予以财政补贴.某商场计划购进A、B两种型号的彩电共l00台,已知该商场所筹购买的资金不少于222000元,但不超过222800元.国家规定这两种型号彩电的进价和售价如下表:
|
型号 |
A |
B |
|
进价(元/台) |
2000 |
2400 |
|
售价(元/台) |
2500 |
3000 |
(1)农民购买哪种型号的彩电获得的政府补贴要多一些?请说明理由;
(2)该商场购进这两种型号的彩电共有哪些方案?其中哪种购迸方案获得的利润最大?请说明理由.(注:利润=售价一进价)
6、(遂宁市2009年)23.某校原有600张旧课桌急需维修,经过A、B、C三个工程队的竞标得知,A、B的工作效率相同,且都为C队的2倍,若由一个工程队单独完成,C队比A 队要多用10天.学校决定由三个工程队一齐施工,要求至多6天完成维修任务.三个工程队都按原来的工作效率施工2天时,学校又清理出需要维修的课桌360张,为了不超过6天时限,工程队决定从第3天开始,各自都提高工作效率,A、B队提高的工作效率仍然都是C队提高的2倍.这样他们至少还需要3天才能成整个维修任务.
⑴求工程队A原来平均每天维修课桌的张数;
⑵求工程队A提高工作效率后平均每天多维修课桌张数的取值范围.
解:⑴设C队原来平均每天维修课桌x张,
根据题意得:
解这个方程得:x=30
经检验x=30是原方程的根且符合题意,2x=60
答:A队原来平均每天维修课桌60张.
⑵设C队提高工效后平均每天多维修课桌x张,施工2天时,已维修(60+60+30)×2=300(张),从第3天起还需维修的张数应为(300+360)=600(张)
根据题意得:
3(2x+2x+x+150)≤660≤4(2x+2x+x+150)
解这个不等式组得::3≤x≤14
∴6≤2x≤28
答:A队提高工效后平均每天多维修的课桌张数的取值范围是:6≤2x≤28
5、(浙江省2009年湖州市)22.(本小题10分)随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加.据统计,某小区2006年底拥有家庭轿车64辆,2008年底家庭轿车的拥有量达到100辆.
(1) 若该小区2006年底到2009年底家庭轿车拥有量的年平均增长率都相同,求该小区到2009年底家庭轿车将达到多少辆?
(2) 为了缓解停车矛盾,该小区决定投资15万元再建造若干个停车位.据测算,建造费用分别为室内车位5000元/个,露天车位1000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,求该小区最多可建两种车位各多少个?试写出所有可能的方案.
解:(1)设家庭轿车拥有量的年平均增长率为 ,则:
,则:
 ,……………2分
,……………2分
解得: %,
%, (不合题意,舍去),……………2分
(不合题意,舍去),……………2分
 .……………1分
.……………1分
答:该小区到2009年底家庭轿车将达到125辆.……………1分
(2)设该小区可建室内车位 个,露天车位
个,露天车位 个,则:
个,则:
 ……………2分
……………2分 
由①得: =150-5
=150-5 代入②得:
代入②得: ,
,
 是正整数,
是正整数, =20或21,
=20或21,
当 时
时 ,当
,当 时
时 .……………2分
.……………2分
 方案一:建室内车位20个,露天车位50个;方案二:室内车位21个,露天车位45个.
方案一:建室内车位20个,露天车位50个;方案二:室内车位21个,露天车位45个.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com