
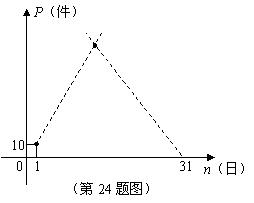
36、(2009湖北孝感)24.(本题满分10分)五月份,某品牌衬衣正式上市销售,5月1日的销售量为10件,5月2日的销售量为35件,以后每天的销售量比前一天多25件,直到日销售量达到最大后,销售量开始逐日下降,至此,每天的销售量比前一天少15件,直到5月31日销售量为0.设该品牌衬衣的日销售量为P(件),销售日期为n(日),P与n之间的关系如图所示.
(1)写出P关于n的函数关系式P= (注明n的取值范围);(3分)
 (2)经研究表明,该品牌衬衣的日销售量超过150件的时间为该品牌衬衣的流行期.请问:该品牌衬衣本月在市面的流行期是多少天?(4分)
(2)经研究表明,该品牌衬衣的日销售量超过150件的时间为该品牌衬衣的流行期.请问:该品牌衬衣本月在市面的流行期是多少天?(4分)
(3)该品牌衬衣本月共销售了 件.(3分)
解:(1)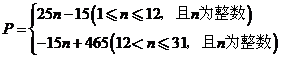 ······················································· 3分
······················································· 3分
(2)由题意,有: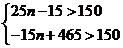 ······································································· 5分
······································································· 5分
解得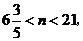 整数
整数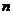 的值可取7,8,9……20共14个.
的值可取7,8,9……20共14个.
∴该品牌衬衣本月在市面的流行期为14天.························································· 7分
(3)4335件.
34、(2009年湖北武汉)23.(本题满分10分)某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨 元(
元( 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为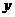 元.
元.
(1)求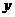 与
与 的函数关系式并直接写出自变量
的函数关系式并直接写出自变量 的取值范围;
的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)每件商品的售价定为多少元时,每个月的利润恰为2200元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元?
解:(1)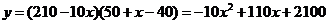 (
(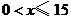 且
且 为整数);
为整数);
(2)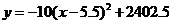 .
.
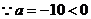 ,
,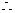 当
当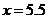 时,
时,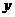 有最大值2402.5.
有最大值2402.5.
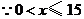 ,且
,且 为整数,
为整数,
当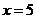 时,
时,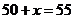 ,
,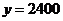 (元),当
(元),当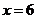 时,
时,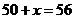 ,
,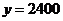 (元)
(元)
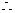 当售价定为每件55或56元,每个月的利润最大,最大的月利润是2400元.
当售价定为每件55或56元,每个月的利润最大,最大的月利润是2400元.
(3)当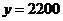 时,
时,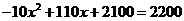 ,解得:
,解得: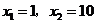 .
.
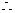 当
当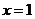 时,
时,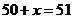 ,当
,当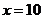 时,
时,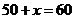 .
.
 当售价定为每件51或60元,每个月的利润为2200元.
当售价定为每件51或60元,每个月的利润为2200元.
当售价不低于51或60元,每个月的利润为2200元.
当售价不低于51元且不高于60元且为整数时,每个月的利润不低于2200元(或当售价分别为51,52,53,54,55,56,57,58,59,60元时,每个月的利润不低于2200元).
35、(2009年湖北仙桃、天门、潜江、江汉油田)22.(本题满分10分)宏志中学九年级300名同学毕业前夕给灾区90名同学捐赠了一批学习用品(书包和文具盒),由于零花钱有限,每6人合买一个书包,每2人合买一个文具盒(每个同学都只参加一件学习用品的购买),书包和文具盒的单价分别是54元和12元.
(1)若有x名同学参加购买书包,试求出购买学习用品的总件数y与x之间的函数关系式(不要求写出自变量的取值范围);
(2)若捐赠学习用品总金额超过了2300元,且灾区90名同学每人至少得到了一件学习用品,请问同学们如何安排购买书包和文具盒的人数?此时选择其中哪种方案,使购买学习用品的总件数最多?
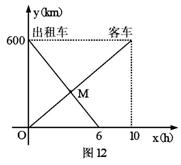
33、(2009湖北黄石)23、(本小题8分)一辆客车从甲地开往甲地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1(km),出租车离甲地的距离为y2(km),客车行驶时间为x(h),y1,y2与x的函数关系图象如图12所示:
(1)根据图象,直接写出y1,y2关于x的函数关系式。
(2)分别求出当x=3,x=5,x=8时,两车之间的距离。
(3)若设两车间的距离为S(km),请写出S关于x的函数关系式。
 (4)甲、乙两地间有A、B两个加油站,相距200km,若客车进入A站加油时,出租车恰好进入B站加油。求A加油站到甲地的距离。
(4)甲、乙两地间有A、B两个加油站,相距200km,若客车进入A站加油时,出租车恰好进入B站加油。求A加油站到甲地的距离。
解:(1)y1=60x(0≤x≤10)
y2=-100x+600(0≤x≤6) ………(1分)
(2)当x=3时 y1=180 y2=300 ∴y2-y1=120
当x=5时 y1=300 y2=100 ∴y1-y2=200
当x=8时 y1=480 y2=0 ∴y1-y2=y1=480 ……(1分)
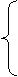 (3)
1600x+600 (0≤x≤
(3)
1600x+600 (0≤x≤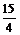 )
)
S= 1600x-600 (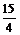 ≤x≤6)
≤x≤6)
60x (6≤x≤10) ………(3分)
(4)由题意得:S=200
①当0≤x≤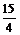 时 -160x+600=200 ∴x=
时 -160x+600=200 ∴x=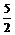 ∴y1=60x=150km
∴y1=60x=150km
②当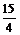 ≤x≤6时 160x-600=200 ∴x=5 ∴y1=300km
≤x≤6时 160x-600=200 ∴x=5 ∴y1=300km
③当6≤x≤10时 60x≥360 不合题意
即:A加油站到甲地距离为150km或300km。 ………(3分)
32、(2009年湖北鄂州)26、(10分)某土产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售。按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满,根据下表提供的信息,
解答以下问题
(1)设装运甲种土特产的车辆数为x,装运乙种土特产的车辆数为y,求y与x之间的函数关系式.
(2)如果装运每种土特产的车辆都不少于3辆,那么车辆的安排方案有几种?并写出每种安排方案。
(3)若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值。
解:(1)8x+6y+5(20-x-y)=120
∴y=20-3x ∴y与x之间的函数关系式为y=20-3x ……………………3分
(2)由x≥3,y=20-3x≥3, 20-x-(20-3x)≥3可得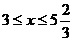
又∵x为正整数 ∴ x=3,4,5 ………………………………………………5分
故车辆的安排有三种方案,即:
方案一:甲种3辆 乙种11辆 丙种6辆
方案二:甲种4辆 乙种8辆 丙种8辆
方案三:甲种5辆 乙种5辆 丙种10辆…………………………7分
(3)设此次销售利润为W元,
W=8x·12+6(20-3x)·16+5[20-x-(20-3x)]·10=-92x+1920
∵W随x的增大而减小 又x=3,4,5
∴ 当x=3时,W最大=1644(百元)=16.44万元
答:要使此次销售获利最大,应采用(2)中方案一,即甲种3辆,乙种11辆,丙种6辆,最大利润为16.44万元。 ……
31、(2009湖北荆州) 24.(10分)由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖.某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台,并预付了5万元押金。他计划一年内要达到一定的销售量,且完成此销售量所用的进货总金额加上押金控制在不低于34万元,但不高于40万元.若一年内该产品的售价
24.(10分)由于国家重点扶持节能环保产业,某种节能产品的销售市场逐渐回暖.某经销商销售这种产品,年初与生产厂家签订了一份进货合同,约定一年内进价为0.1万元/台,并预付了5万元押金。他计划一年内要达到一定的销售量,且完成此销售量所用的进货总金额加上押金控制在不低于34万元,但不高于40万元.若一年内该产品的售价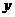 (万元/台)与月次
(万元/台)与月次 (
(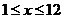 且为整数)满足关系是式:
且为整数)满足关系是式: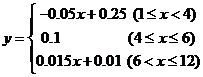 ,一年后发现实际每月的销售量
,一年后发现实际每月的销售量 (台)与月次
(台)与月次 之间存在如图所示的变化趋势.
之间存在如图所示的变化趋势.
⑴ 直接写出实际每月的销售量 (台)与月次
(台)与月次 之间
之间
的函数关系式;
⑵ 求前三个月中每月的实际销售利润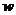 (万元)与月
(万元)与月
次 之间的函数关系式;
之间的函数关系式;
⑶ 试判断全年哪一个月的的售价最高,并指出最高售价;
⑷ 请通过计算说明他这一年是否完成了年初计划的销售量.
30、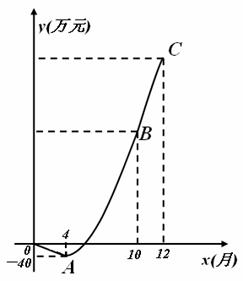 (2009湖北黄冈)(满分11分)新星电子科技公司积极应对2008年世界金融危机,及时调整投资方向,瞄准光伏产业,建成了太阳能光伏电池生产线.由于新产品开发初期成本高,且市场占有率不高等因素的影响,产品投产上市一年来,公司经历了由初期的亏损到后来逐步盈利的过程(公司对经营的盈亏情况每月最后一天结算1次).公司累积获得的利润y(万元)与销售时间第x(月)之间的函数关系式(即前x个月的利润总和y与x之间的关系)对应的点都在如图所示的图象上.该图象从左至右,依次是线段OA、曲线AB和曲线BC,其中曲线AB为抛物线的一部分,点A为该抛物线的顶点,曲线BC为另一抛物线
(2009湖北黄冈)(满分11分)新星电子科技公司积极应对2008年世界金融危机,及时调整投资方向,瞄准光伏产业,建成了太阳能光伏电池生产线.由于新产品开发初期成本高,且市场占有率不高等因素的影响,产品投产上市一年来,公司经历了由初期的亏损到后来逐步盈利的过程(公司对经营的盈亏情况每月最后一天结算1次).公司累积获得的利润y(万元)与销售时间第x(月)之间的函数关系式(即前x个月的利润总和y与x之间的关系)对应的点都在如图所示的图象上.该图象从左至右,依次是线段OA、曲线AB和曲线BC,其中曲线AB为抛物线的一部分,点A为该抛物线的顶点,曲线BC为另一抛物线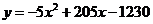 的一部分,且点A,B,C的横坐标分别为4,10,12
的一部分,且点A,B,C的横坐标分别为4,10,12
(1)求该公司累积获得的利润y(万元)与时间第x(月)之间的函数关系式;
(2)直接写出第x个月所获得S(万元)与时间x(月)之间的函数关系式(不需要写出计算过程);
(3)前12个月中,第几个月该公司所获得的利润最多?最多利润是多少万元?
29、(黑龙江哈尔滨)26.(本题8分) 跃壮五金商店准备从宁云机械厂购进甲、乙两种零件进行销售.若每个甲种零件的进价比每个乙种零件的进价少2元,且用80元购进甲种零件的数量与用100元购进乙种零件的数量相同.
(1)求每个甲种零件、每个乙种零件的进价分别为多少元?
(2)若该五金商店本次购进甲种零件的数量比购进乙种零件的数量的3倍还少5个,购进两种零件的总数量不超过95个,该五金商店每个甲种零件的销售价格为12元,每个乙种零件的销售价格为15元,则将本次购进的甲、乙两种零件全部售出后,可使销售两种零件的总利润(利润=售价-进价)超过371元,通过计算求出跃壮五金商店本次从宁云机械厂购进甲、乙两种零件有几种方案?请你设计出来.

28、(2009河北)25.(本小题满分12分)某公司装修需用A型板材240块、B型板材180块,A型板材规格是60 cm×30 cm,B型板材规格是40 cm×30 cm.现只能购得规格是150 cm×30 cm的标准板材.一张标准板材尽可能多地裁出A型、B型板材,共有下列三种裁法:(图15是裁法一的裁剪示意图)
|
|
裁法一 |
裁法二 |
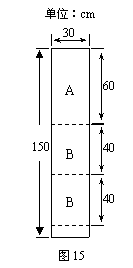 裁法三 裁法三 |
|
A型板材块数 |
1 |
2 |
0 |
|
B型板材块数 |
2 |
m |
n |
设所购的标准板材全部裁完,其中按裁法一裁x张、按裁法二裁y
张、按裁法三裁z张,且所裁出的A、B两种型号的板材刚好够用.
(1)上表中,m = ,n = ;
(2)分别求出y与x和z与x的函数关系式;
(3)若用Q表示所购标准板材的张数,求Q与x的函数关系式,
并指出当x取何值时Q最小,此时按三种裁法各裁标准板材
多少张?
解:(1)0 ,3.
(2)由题意,得
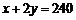 , ∴
, ∴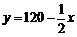 .
. 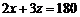 ,∴
,∴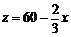 .
.
(3)由题意,得 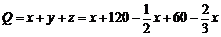 .整理,得
.整理,得 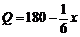 .
.
由题意,得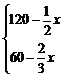 解得 x≤90.
解得 x≤90.
[注:事实上,0≤x≤90 且x是6的整数倍]由一次函数的性质可知,当x=90时,Q最小.此时按三种裁法分别裁90张、75张、0张.
27、(2009年贵州安顺)24、(本题满分10分)在“五一”期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
(1) 小明他们一共去了几个成人,几个学生?
(2) 请你帮助小明算一算,用哪种方式购票更省钱?说明理由。

解:(1)设成人人数为x人,则学生人数为(12-x)人. 则 (1′)
35x + 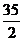 (12 –x)=
350
(4′)
(12 –x)=
350
(4′)
解得:x = 8 (7′)
故:学生人数为12 – 8 = 4 人, 成人人数为8人. (8′)
(2)如果买团体票,按16人计算,共需费用:
35×0.6×16 = 336元
336﹤350 所以,购团体票更省钱。 (10′)
答:有成人8人,学生4人;购团体票更省钱。
26、(黔东南州2009年)25、(12分)凯里市某大型酒店有包房100间,在每天晚餐营业时间,每间包房收包房费100元时,包房便可全部租出;若每间包房收费提高20元,则减少10间包房租出,若每间包房收费再提高20元,则再减少10间包房租出,以每次提高20元的这种方法变化下去。
(1)设每间包房收费提高x(元),则每间包房的收入为y1(元),但会减少y2间包房租出,请分别写出y1、y2与x之间的函数关系式。
(2)为了投资少而利润大,每间包房提高x(元)后,设酒店老板每天晚餐包房总收入为y(元),请写出y与x之间的函数关系式,求出每间包房每天晚餐应提高多少元可获得最大包房费收入,并说明理由。
解:(1)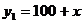 ………………(1分)
………………(1分)
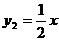 ……………………(3分)
……………………(3分)
(2)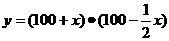 ………………(6分)
………………(6分)
即:y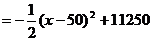 …………………(8分)
…………………(8分)
因为提价前包房费总收入为100×100=10000。
当x=50时,可获最大包房收入11250元,因为11250>10000。又因为每次提价为20元,所以每间包房晚餐应提高40元或60元。…………(12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com