
1.如果α∈(,π),且sinα=,那么sin(α+)+cos(α+)= ( )
A. B.- C. D.-
解析:∵sinα=,<α<π,∴cosα=-,而sin(α+)+cos(α+)=sin(α+)=
cosα=-.
答案:D
4.两个平面垂直的性质.
3.应用两个平面垂直的判定定理的关键是将面面垂直的问题转化为线面垂直的问题;
2.两个平面垂直的判定方法(判定方法有两种,一是利用定义,二是利用判定定理.)
1.两个平面垂直的定义、画法
3.如图,正方体的棱长为1, ,求:
,求:
(1) 与
与 所成角;
所成角;
(2) 与平面
与平面 所成角的正切值;
所成角的正切值;
(3)平面 与平面
与平面 所成角
所成角
解:(1)∵ ∴
∴ 与
与 所成角就是
所成角就是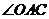
∵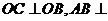 平面
平面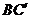 ∴
∴ (三垂线定理)
(三垂线定理)
在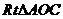 中,
中, 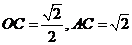 ∴
∴
(2)作 ,平面
,平面 平面
平面
∴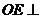 平面
平面 ,
,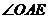 为
为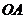 与平面
与平面 所成角
所成角
在 中,
中,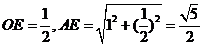 ∴
∴
(3)∵ ∴
∴ 平面
平面
又∵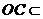 平面
平面 ∴平面
∴平面 平面
平面
即平面 与平面
与平面 所成角为
所成角为

说明:本题包含了线线角,线面角和面面角三类问题,求角度问题主要是求两条异面直线所成角 ,直线和平面所成角
,直线和平面所成角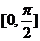 ,二面角
,二面角 三种;求角度问题解题的一般步骤是:(1)找出这个角;(2)证明该角符合题意;(3)作出这个角所在的三角形,解三角形,求出角;求角度问题不论哪种情况都归结到两条直线所成角问题,即在线线成角中找到答案
三种;求角度问题解题的一般步骤是:(1)找出这个角;(2)证明该角符合题意;(3)作出这个角所在的三角形,解三角形,求出角;求角度问题不论哪种情况都归结到两条直线所成角问题,即在线线成角中找到答案
2.如果二面角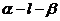 的平面角是锐角,点
的平面角是锐角,点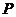 到
到 的距离分别为
的距离分别为
 ,求二面角的大小
,求二面角的大小
分析:点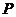 可能在二面角
可能在二面角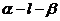 内部,也可能在外部,应区别处理
内部,也可能在外部,应区别处理
解:如图1是点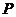 在二面角
在二面角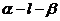 的内部时,图2是点
的内部时,图2是点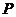 在二面角
在二面角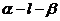 外部时,
外部时,
 ∵
∵ ∴
∴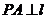
∵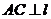 ∴面
∴面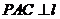
同理,面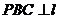
而面 面
面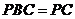
∴面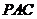 与面
与面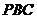 应重合
应重合
即 在同一平面内,
在同一平面内,
则 是二面角
是二面角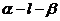 的平面角
的平面角
在 中,
中, ∴
∴
在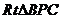 中,
中, ∴
∴
故 (图1)或
(图1)或 (图2)
(图2)
 即二面角
即二面角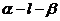 的大小为
的大小为 或
或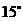

说明:作一个垂直于棱的平面,此平面与两个半平面的交线所成的角就是二面角的平面角
1.直角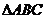 的斜边
的斜边 在平面
在平面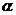 内,
内,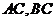 与
与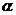 所成角分别为
所成角分别为 ,
, 是斜边
是斜边 上的高线,求
上的高线,求 与平面
与平面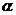 所成角的正弦值
所成角的正弦值
解:过点 作
作 于点
于点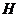 ,连接
,连接 ,
,
则 ,
, ,
, 为所求
为所求 与
与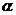 所成角,记为
所成角,记为 ,
,
 令
令 ,则
,则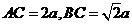 ,
,
则在 中,有
中,有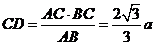
在 中,
中,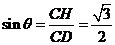
∴ 与平面
与平面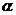 所成角的正弦值
所成角的正弦值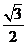 .
.
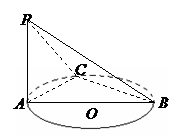 例1
例1  如图,已知
如图,已知 是圆
是圆 的直径,
的直径, 垂直于
垂直于 所在的平面,
所在的平面, 是圆周上不同于
是圆周上不同于 的任一点,求证:平面
的任一点,求证:平面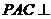 平面
平面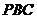 .
.
分析:根据“面面垂直”的判定定理,要证明两平面互相垂直,只要在其中一个平面中寻找一条与另一平面垂直的直线即可
解:∵ 是圆
是圆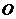 的直径,∴
的直径,∴ ,
,
又∵ 垂直于
垂直于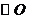 所在的平面,∴
所在的平面,∴ ,
,
∴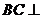 平面
平面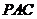 ,又
,又 在平面
在平面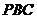 中,
中,
所以,平面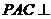 平面
平面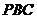 .
.
说明:由于平面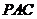 与平面
与平面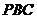 相交于
相交于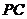 ,所以如果平面
,所以如果平面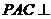 平面
平面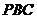 ,则在平面
,则在平面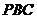 中,垂直于
中,垂直于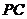 的直线一定垂直于平面
的直线一定垂直于平面 ,这是寻找两个平面的垂线的常用方法
,这是寻找两个平面的垂线的常用方法
例2.已知 ,求证:
,求证: .
.
证明:设 ,
,
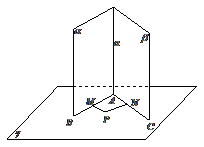 在
在 内取点
内取点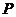 ,过
,过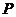 作
作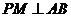 于
于 ,
,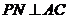 于点
于点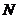 ,
,
∵ ,∴
,∴ ,
,
又∵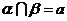 ,
,
∴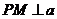 ,同理可得
,同理可得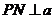 ,
,
∴ .
.
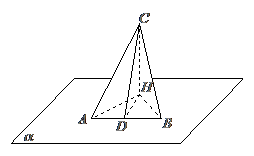
 例3.已知在一个
例3.已知在一个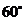 的二面角的棱长有两点
的二面角的棱长有两点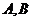 ,
,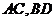 分别是在这个二面角的两个平面内,且垂直于线段
分别是在这个二面角的两个平面内,且垂直于线段 ,又知
,又知 ,求
,求 的长
的长
解:由已知
 ,
,
∴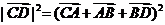


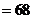 ,
,

3.两平面垂直的性质定理: 若两个平面互相垂直,那么在一个平面内垂直于它们的交线的直线垂直于另一个平面
已知: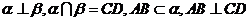 于点
于点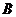 ,
,
求证: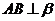 .(面面垂直
.(面面垂直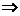 线面垂直)
线面垂直)
证明:在 内过
内过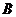 作
作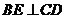 ,则由题意得
,则由题意得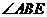 是
是 的平面角,
的平面角,
∵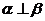 知
知 ,又∵
,又∵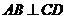 , ∴
, ∴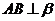 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com