
8.加工某种零件需经过三道工序,设第一、二、三道工序的合格率分别为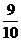 、
、 、
、 ,
,
且各道工序互不影响.
(Ⅰ)求该种零件的合格率;
(Ⅱ)从该种零件中任取3件,求恰好取到一件合格品的概率和至少取到一件合格品的概率.
(Ⅰ)解: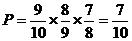 ;
;
(Ⅱ)解法一: 该种零件的合格品率为 ,由独立重复试验的概率公式得:
,由独立重复试验的概率公式得:
恰好取到一件合格品的概率为 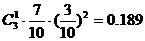 ,
,
至少取到一件合格品的概率为 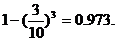
解法二:
恰好取到一件合格品的概率为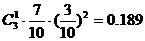 ,
,
至少取到一件合格品的概率为
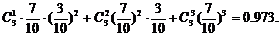
6.一个通讯小组有两套设备,只要其中有一套设备能正常工作,就能进行通讯.每套设备由3个部件组成,只要其中有一个部件出故障,这套设备就不能正常工作.如果在某一时间段内每个部件不出故障的概率为p,计算在这一时间段内,
(1)恰有一套设备能正常工作的概率;
(2)能进行通讯的概率.
解:记“第一套通讯设备能正常工作”为事件A,“第二套通讯设备能正常工作”为事件B.
由题意知P(A)=p3,P(B)=p3,
P( )=1-p3,P(
)=1-p3,P(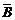 )=1-p3.
)=1-p3.
(1)恰有一套设备能正常工作的概率为P(A·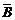 +
+  ·B)=P(A·
·B)=P(A·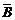 )+P(
)+P( ·B)
·B)
=p3(1-p3)+(1-p3)p3=2p3-2p6.
(2)方法一:两套设备都能正常工作的概率为
P(A·B)=P(A)·P(B)=p6.
至少有一套设备能正常工作的概率,即能进行通讯的概率为
P(A·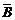 +
+  ·B)+P(A·B)=2p3-2p6+p6=2p3-p6.
·B)+P(A·B)=2p3-2p6+p6=2p3-p6.
方法二:两套设备都不能正常工作的概率为
P( ·
·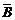 )=P(
)=P( )·P(
)·P(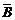 )=(1-p3)2.
)=(1-p3)2.
至少有一套设备能正常工作的概率,
即能进行通讯的概率为1-P( ·
·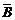 )=1-P(
)=1-P( )·P(
)·P(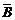 )=1-(1-p3)2=2p3-p6.
)=1-(1-p3)2=2p3-p6.
答:恰有一套设备能正常工作的概率为2p3-2p6,能进行通讯的概率为2p3-p6.
(2005年高考·浙江卷·文17)袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是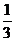 ,从B中摸出一个红球的概率为p.
,从B中摸出一个红球的概率为p.
(Ⅰ) 从A中有放回地摸球,每次摸出一个,共摸5次.(i)恰好有3次摸到红球的概率;(ii)第一次、第三次、第五次摸到红球的概率.
(Ⅱ) 若A、B两个袋子中的球数之比为12,将A、B中的球装在一起后,从中摸出一个红球的概率是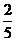 ,求p的值.
,求p的值.
解:(Ⅰ)(ⅰ) 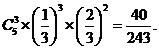
(ⅱ)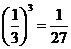 .
.
(Ⅱ)设袋子A中有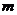 个球,袋子B中有
个球,袋子B中有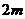 个球,
个球,
由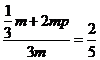 ,得
,得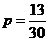
例6 在资料室中存放着书籍和杂志,任一读者借书的概率为0 2,而借杂志的概率为0
2,而借杂志的概率为0 8,设每人只借一本,现有五位读者依次借阅,
8,设每人只借一本,现有五位读者依次借阅,
计算:(1)5人中有2人借杂志的概率
(2)5人中至多有2人借杂志的概率
解:记“一位读者借杂志”为事件A,则“此人借书”为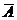 ,5位读者各借一次可看作n次独立重复事件,因此:
,5位读者各借一次可看作n次独立重复事件,因此:
(1)5人中有2人借杂志的概率
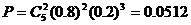
(2)5人中至多有2人借杂志,包括三种情况:5人都不借杂志,5人中恰有1人借杂志,5人中恰有2人借杂志,因此所求概率


例2:有外形相同的球分别装在三个不同的盒子中,每个盒子中有10个小球。其中第一个盒子中有7个球标有字母A,3个球标有字母B;第二个盒子中有红球和白球各5个;第三个盒子中有红球8个,白球2个。试验按如下规则进行:先在第一个盒子中任取一球,若取得标有字母A的球,则在第二个盒子中任取一球;若第一次取得标有字母B的球,则在第三个盒子中任取一球。如果第二次取得的球是红球,则称试验成功,求试验成功的概率。
解:设事件A:从第一个盒子中取得一个标有字母A的球;事件B:从第一个盒子中取得标有字母B的球,则A、B互斥,且P(A)= ,P(B)=
,P(B)= ;事件C:从第二个盒子中取一个红球,事件D:从第三个盒子中取一个红球,则C、D互斥,且P(C)=
;事件C:从第二个盒子中取一个红球,事件D:从第三个盒子中取一个红球,则C、D互斥,且P(C)=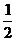 ,P(D)=
,P(D)= 。
。
显然,事件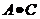 与事件
与事件 互斥,且事件A与C是相互独立的,B与D也是相互独立的。所以试验成功的概率为
互斥,且事件A与C是相互独立的,B与D也是相互独立的。所以试验成功的概率为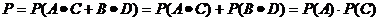 +
+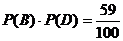
 本次试验成功的概率为
本次试验成功的概率为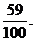
思维点拨:对题中出现的事件进行正确分类与重组是解题的关键。
例3:甲、乙、丙3人各进行一次射击,如果甲、乙2人击中目标的概率是0.8,丙击中目标的概率是0.6,计算:(1)3人都击中目标的概率; (2)至少有2人击中目标的概率;
(3)其中恰有1人击中目标的概率.
解:(1)记“甲、乙、丙各射击一次,击中目标”分别为事件A、B、C彼此独立,三人都击中目标就是事件A·B·C发生,根据相互独立事件的概率乘法公式得:
P(A·B·C)=P(A)·P(B)·P(C)=0.8×0.8×0.6=0.384
(2)至少有2人击中目标包括两种情况:一种是恰有2人击中,另一种是3人都击中,其中恰有2人击中,又有3种情形,即事件A·B· ,A·
,A· ·C,
·C, ·B·C分别发生,而这3种事件又
·B·C分别发生,而这3种事件又
互斥,
故所求的概率是P(A·B· )+P(A·
)+P(A· ·C)+P(
·C)+P( ·B·C)+P(A·B·C)
·B·C)+P(A·B·C)
P(A) ·P(B)·P( )+P(A) ·P(
)+P(A) ·P( )·P(C)+P(
)·P(C)+P( )·P(B) ·P(C)+P(A) ·P(B) ·P(C)
)·P(B) ·P(C)+P(A) ·P(B) ·P(C)
=0.8×0.8×0.4+0.8×0.2×0.6+0.2×0.8×0.6+0.8×0.8×0.6=0.832
(3)恰有1人击中目标有3种情况,即事件A· ·
·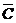 ,
,  ·B·
·B·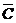 ,
,  ·
· ·C,且事件分别互斥,故所求的概率是P(A·
·C,且事件分别互斥,故所求的概率是P(A· ·
·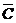 )+P(
)+P( ·B·
·B·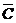 )+P(
)+P( ·
· ·C)
·C)
= P(A)·P( )·P(
)·P(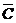 )+P(
)+P( )·P(B) ·P(
)·P(B) ·P(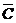 )+P(
)+P( )·P(
)·P( )·P(C)
)·P(C)
=0.8×0.2×0.4+0.2×0.8×0.4+0.2×0.2×0.6=0.152.
说明:题(3)还可用逆向思考,先求出3人都未击中的概率是0.016,再用1-0.832-0.016可得
练习:设每门高射炮命中飞机的概率为0.6,试求:
(1)两门高射炮同时射击一发炮弹而命中飞机的概率;
(2)若今有一飞机来犯,问需要多少门高射炮射击,才能以至少99%的概率命中它?
解:(1)P=0.84
(2)设需要n门高射炮才能达目的,用A表示“命中飞机”这一事件,用Ai表示“第i门高射炮命中飞机”,则A1、A2…An相互独立,故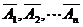 也相互独立,故P(A)=1-P(
也相互独立,故P(A)=1-P( )=1-P(
)=1-P(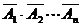 )=1-P(
)=1-P( )P(
)P(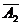 )…P(
)…P(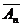 )=1-
)=1- .据题意P(A)≥0.99,∴1-
.据题意P(A)≥0.99,∴1- ≥99%,得n≥5.02.
≥99%,得n≥5.02.
答:至少需6门高射炮才能以99%的概率命中。
思维点拨: 本题若用直接法就不可能求解,故转化为间接考虑。
[例4]A、B两位同学各有五张卡片,现以投掷均匀硬币的形式进行游戏,当出现正面朝上时A赢得B一张卡片,否则B赢得A一张卡片,如果某人已赢得所有卡片,则游戏终止.求掷硬币的次数不大于7次时游戏终止的概率.
解:设 表示游戏终止时掷硬币的次数,
表示游戏终止时掷硬币的次数,
设正面出现的次数为m,反面出现的次数为n,则 ,可得:
,可得:
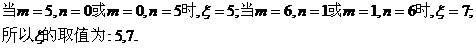
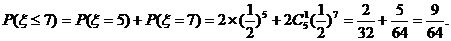
(2005年高考·全国卷II·文18)
甲、乙两队进行一场排球比赛,根据以往经验,单局比赛甲队胜乙队的概率为0.6,本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束,设各局比赛相互间没有影响,求
(Ⅰ)前三局比赛甲队领先的概率;
(Ⅱ)本场比赛乙队以3:2取胜的概率.(精确到0.001)
本小题主要考查相互独立事件概率的计算,运用概率知识解决实际问题的能力。满分12分
解:单局比赛甲队胜乙队的概率为0.6,乙队胜甲队的概率为1-0.6=0.4
(Ⅰ)记“甲队胜三局”为事件A,“甲队胜二局”为事件B,则
P(A)=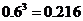 ,P(B)=
,P(B)=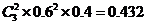
所以前三局比赛甲队领先的概率为P(A)+P(B)=0.648
(Ⅱ)若本场比赛乙队3:2取胜,则前四局双方应以2:2战平,且第五局乙队胜,所以所求事件的概率为
(2005全国卷Ⅲ设甲、乙、丙三台机器是否需要照顾相互之间没有影响.已知在某一小时内,甲、乙都需要照顾的概率为0.05,甲、丙都需要照顾的概率为0.1,乙、丙都需要照顾的概率为0.125,
(Ⅰ)求甲、乙、丙每台机器在这个小时内需要照顾的概率分别是多少;
(Ⅱ)计算这个小时内至少有一台需要照顾的概率.
解:记“机器甲需要照顾”为事件A,“机器乙需要照顾”为事件B,“机器丙需要照顾”为事件C,由题意.各台机器是否需要照顾相互之间没有影响,因此,A,B,C是相互独立事件
(Ⅰ)由题意得: P(A·B)=P(A)·P(B)=0.05
P(A·C)=P(A)·P(C)=0.1
P(B·C)=P(B)·P(C)=0.125
解得:P(A)=0.2;P(B)=0.25;P(C)=0.5
所以, 甲、乙、丙每台机器需要照顾的概率分别是0.2、0.25、0.5
(Ⅱ)记A的对立事件为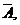 B的对立事件为
B的对立事件为 ,C的对立事件为
,C的对立事件为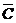 ,
,
则 ,
,
于是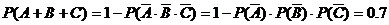
所以这个小时内至少有一台机器需要照顾的概率为0.7.
10.(2005江苏)甲、乙两人各射击一次,击中目标的概率分别是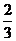 和
和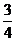 。假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响。
。假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响。
(Ⅰ)求甲射击4次,至少1次未击中目标的概率;
(Ⅱ)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(Ⅲ)假设两人连续两次未击中目标,则停止射击。问:乙恰好射击5次后,被中止射击的概率是多少?
解:(Ⅰ)记“甲连续射击4次,至少1次未击中目标”为事件A1,由题意,射击4次,相当于4次独立重复试验,故P(A1)=1- P( )=1-
)=1- =
=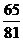 。
。
答:甲射击4次,至少1次未击中目标的概率为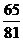 ;
;
(Ⅱ) 记“甲射击4次,恰好击中目标2次”为事件A2,“乙射击4次,恰好击中目标3次”为事件B2,则
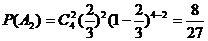 ,
,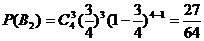 ,
,
由于甲、乙设计相互独立,故 。
。
答:两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率为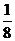 ;
;
(Ⅲ)记“乙恰好射击5次后,被中止射击”为事件A3,“乙第i次射击为击中” 为事件Di,(i=1,2,3,4,5),则A3=D5D4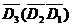 ,且P(Di)=
,且P(Di)= ,由于各事件相互独立,故P(A3)= P(D5)P(D4)P(
,由于各事件相互独立,故P(A3)= P(D5)P(D4)P(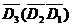 )=
)= ×
× ×
×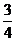 ×(1-
×(1- ×
× )=
)=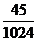 , 答:乙恰好射击5次后,被中止射击的概率是
, 答:乙恰好射击5次后,被中止射击的概率是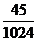 。
。
[探索题](2004湖南)甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为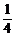 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为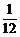 ,甲、丙两台机床加工的零件都是一等品的概率为
,甲、丙两台机床加工的零件都是一等品的概率为 .
.
(1)分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
(2)从甲、乙、丙加工的零件中各取一个检验,求至少有一个一等品的概率.
解:(1)设A、B、C分别为甲、乙、丙三台机床各自加工的零件是一等品的事件,
由题设条件有:
|
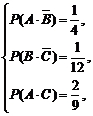 即
即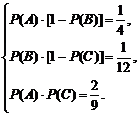
由①③得P(B)=1-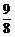 P(C),
P(C),
代入②得27[P(C)]2-51P(C)+22=0.
解得P(C)=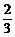 或
或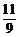 (舍去).
(舍去).
将P(C)=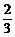 分别代入③②可得P(A)=
分别代入③②可得P(A)=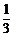 ,P(B)=
,P(B)=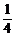 ,
,
即甲、乙、丙三台机床各自加工的零件是一等品的概率分别是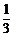 ,
,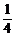 ,
,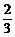 .
.
(2)记D为从甲、乙、丙加工的零件中各取一个检验至少有一个一等品的事件,则
P(D)=1-P( )=1-[1-P(A)][1-P(B)][1-P(C)]=1-
)=1-[1-P(A)][1-P(B)][1-P(C)]=1-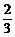 ·
·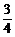 ·
·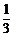 =
= .
.
故从甲、乙、丙加工的零件中各取一个检验,至少有一个一等品的概率为 .
.
备选题:
9.9粒种子分种在甲、乙、丙3个坑内,每坑3粒,每粒种子发芽的概率为0.5. 若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没发芽,则这个坑需要补种.
(Ⅰ)求甲坑不需要补种的概率;
(Ⅱ)求3个坑中恰有1个坑不需要补种的概率;
(Ⅲ)求有坑需要补种的概率.(精确到0.001)
解:(Ⅰ)因为甲坑内的3粒种子都不发芽的概率为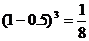 ,所以甲坑不需要补种的概率为
,所以甲坑不需要补种的概率为 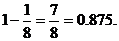
(Ⅱ)3个坑恰有一个坑不需要补种的概率为 
(Ⅲ)法一:因为3个坑都不需要补种的概率为 ,
,
所以有坑需要补种的概率为 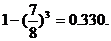
法二:3个坑中恰有1个坑需要补种的概率为
恰有2个坑需要补种的概率为 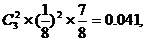
3个坑都需要补种的概率为 
所以有坑需要补种的概率为 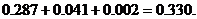
8. 假设每一架飞机引擎在飞行中故障率为1-P,且各引擎是否故障是独立的,如果至少50%的引擎能正常运行,飞机就可以成功地飞行,问对于多大的P而言,4引擎飞机比2引擎的飞机更为安全?
分析:4引擎飞机可以看作4次独立重复试验,要能正常运行,即求发生k次(k≥2)的概率.同理,2引擎飞机正常运行的概率即是2次独立重复试验中发生k次(k≥1)的概率,由此建立不等式求解.
解:4引擎飞机成功飞行的概率为
C P2(1-P)2+C
P2(1-P)2+C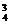 P3(1-P)+C
P3(1-P)+C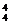 P4=6P2(1-P)2+4P3(1-P)+P4.
P4=6P2(1-P)2+4P3(1-P)+P4.
2引擎飞机成功飞行的概率为C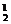 P(1-P)+C
P(1-P)+C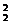 P2=2P(1-P)+P2.
P2=2P(1-P)+P2.
要使4引擎飞机比2引擎飞机安全,只要
6P2(1-P)2+4P3(1-P)+P4≥2P(1-P)+P2.
化简,分解因式得(P-1)2(3P-2)≥0.
所以3P-2≥0,即得P≥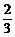 .
.
答:当引擎不出故障的概率不小于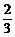 时,4引擎飞机比2引擎飞机安全.
时,4引擎飞机比2引擎飞机安全.
7.(2006北京)某公司招聘员工,指定三门考试课程,有两种考试方案.
方案一:考试三门课程,至少有两门及格为考试通过;
方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.
假设某应聘者对三门指定课程考试及格的概率分别是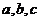 ,且三门课程考试是否及格相互之间没有影响.
,且三门课程考试是否及格相互之间没有影响.
(Ⅰ)分别求该应聘者用方案一和方案二时考试通过的概率;
(Ⅱ)试比较该应聘者在上述两种方案下考试通过的概率的大小.(说明理由)
解:记该应聘者对三门指定课程考试及格的事件分别为A,B,C.
则P(A)= a,P(B)= b,P(C)= c
(Ⅰ) 应聘者用方案一考试通过的概率

应聘者用方案二考试通过的概率
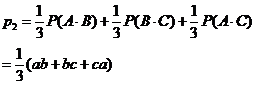
(Ⅱ)因为a,b,c∈[0, 1],所以

故p1≥p2, 即采用第一种方案,该应聘者考试通过的概率较大.
6.法一:放1个球,被放入1号盒的概率为P=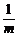 .n个球放入m个不同的盒子内相当于做n次独立重复试验. Pn(r)=C
.n个球放入m个不同的盒子内相当于做n次独立重复试验. Pn(r)=C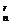 ·(
·(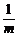 )r·(1-
)r·(1-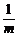 )n-r=
)n-r=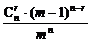 .
.
法二:把n个不同的球任意放入m个不同的盒子内共有mn个等可能的结果.其中1号盒内恰有r个球的结果数为C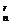 (m-1)n-r,故所求概率P(A)=
(m-1)n-r,故所求概率P(A)= .
.
[解答题]
6. 把n个不同的球随机地放入编号为1,2,…,m的m个盒子内,则1号盒恰有r个球的概率等于__________.
简答.提示:1-3.BDC; 3.由C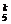 (
(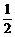 )k(
)k(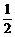 )5-k=C
)5-k=C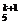 (
(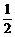 )k+1·(
)k+1·(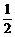 )5-k-1,
)5-k-1,
即C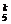 =C
=C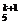 ,k+(k+1)=5,k=2; 4.他须解对5题或4题.P=(
,k+(k+1)=5,k=2; 4.他须解对5题或4题.P=(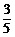 )5+C
)5+C ×(
×(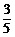 )4×(1-
)4×(1-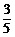 )=
)=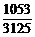 ; 5.
; 5. ;
;
5.甲、乙两人在罚球线投球命中的概率分别为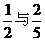 ,甲、乙两人在罚球线各投球二次,这四次中至少一次命中的概率是________.
,甲、乙两人在罚球线各投球二次,这四次中至少一次命中的概率是________.
4.某学生参加一次选拔考试,有5道题,每题10分.已知他解题的正确率为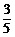 ,若40分为最低分数线,则该生被选中的概率是________.
,若40分为最低分数线,则该生被选中的概率是________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com