
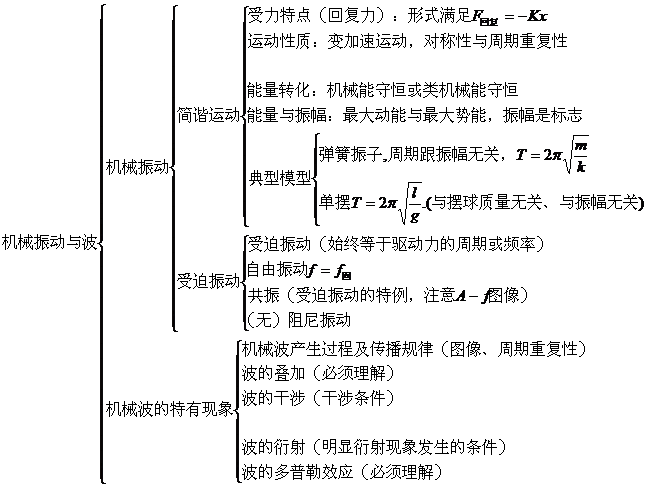 二、难点与突破
二、难点与突破
1、振动
(1)简谐运动:简谐运动中的力学运动学条件及位移,回复力,振幅,周期,频率及在一次全振动过程中各物理量的变化规律。
简谐振动: 回复力: F = 一KX 加速度:a =一KX/m
单摆:T= 2 (与摆球质量,振幅无关) *弹簧振子T= 2
(与摆球质量,振幅无关) *弹簧振子T= 2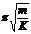 (与振子质量有关,与振幅无关)
(与振子质量有关,与振幅无关)
等效摆长、等效的重力加速度 影响重力加速度有:
①纬度,离地面高度
②在不同星球上不同,与万有引力圆周运动规律(或其它运动规律)结合考查
③系统的状态(超、失重情况)
④所处的物理环境有关,有电磁场时的情况
⑤静止于平衡位置时等于摆线张力与球质量的比值
注意等效单摆(即是受力环境与单摆的情况相同)
(2)共振的现象、条件、防止和应用
11.已知椭圆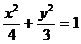 ,能否在此椭圆位于
,能否在此椭圆位于 轴左侧的部分上找到一点
轴左侧的部分上找到一点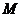 ,使它到左准线的距离为它到两焦点
,使它到左准线的距离为它到两焦点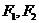 距离的等比中项,若能找到,求出该点的坐标,若不能找到,请说明理由.
距离的等比中项,若能找到,求出该点的坐标,若不能找到,请说明理由.
10. (05全国卷Ⅰ))已知椭圆的中心为坐标原点O,焦点在 轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,
轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点, 与
与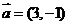 共线。
共线。
(Ⅰ)求椭圆的离心率;
(Ⅱ)设M为椭圆上任意一点,且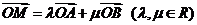 ,证明
,证明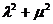 为定值
为定值
8.已知椭圆 的离心率
的离心率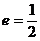 ,则
,则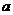 的值等于 _________.
的值等于 _________.
9 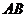 是椭圆
是椭圆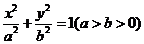 中不平行于对称轴的一条弦,
中不平行于对称轴的一条弦,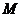 是
是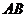 的中点,
的中点,
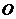 是椭圆的中心,求证:
是椭圆的中心,求证: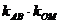 为定值.
为定值.
5. (05山东卷)设直线 关于原点对称的直线为
关于原点对称的直线为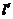 ,若
,若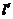 与椭圆
与椭圆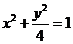 的交点为A、B、,点
的交点为A、B、,点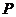 为椭圆上的动点,则使
为椭圆上的动点,则使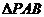 的面积为
的面积为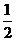 的点
的点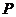 的个数为(
)
的个数为(
)
(A)1 (B)2 (C)3 (D)4
6椭圆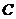 与椭圆
与椭圆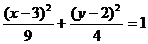 ,关于直线
,关于直线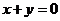 对称,则椭圆
对称,则椭圆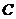 的方程是_______.
的方程是_______.
7到两定点 的距离和等于
的距离和等于 的点的轨迹方程是
.
的点的轨迹方程是
.
4.(05天津卷)从集合{1,2,3…,11}中任选两个元素作为椭圆方程 中的m和n,则能组成落在矩形区域B={(x,y)| |x|<11且|y|<9}内的椭圆个数为( )
中的m和n,则能组成落在矩形区域B={(x,y)| |x|<11且|y|<9}内的椭圆个数为( )
A.43 B. 72 C. 86 D. 90
3.已知椭圆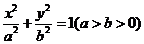 的左焦点为
的左焦点为 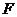 ,
,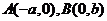 为椭圆的两个顶点,若
为椭圆的两个顶点,若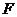 到
到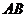 的距离等于
的距离等于 ,则椭圆的离心率为
( )
,则椭圆的离心率为
( )
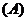

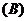
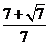
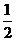
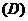
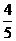
2. 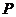 是椭圆
是椭圆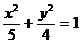 上的一点,
上的一点,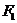 和
和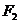 是焦点,若∠F1PF2=30°,则△F1PF2的面积等于 (
)
是焦点,若∠F1PF2=30°,则△F1PF2的面积等于 (
)

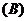
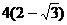
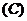
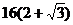
1.(05重庆卷) 若动点(x,y)在曲线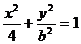 (b>0)上变化,则x22y的最大值( )
(b>0)上变化,则x22y的最大值( )
(A)  ; (B)
; (B) 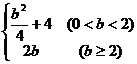 ;
;
(C) 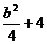 ; (D) 2b
; (D) 2b
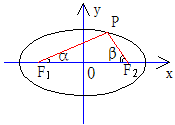
例1(05浙江) .如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|∶|A1F1|=2∶1.
(Ⅰ)求椭圆的方程;
 (Ⅱ)若直线l1:x=m(|m|>1),P为l1上的动点,使∠F1PF2最大的点P记为Q,求点Q的坐标(用m表示).
(Ⅱ)若直线l1:x=m(|m|>1),P为l1上的动点,使∠F1PF2最大的点P记为Q,求点Q的坐标(用m表示).
例2设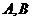 是两个定点,且
是两个定点,且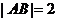 ,动点
,动点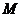 到
到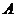 点的距离是
点的距离是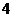 ,线段
,线段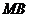 的垂直平分线
的垂直平分线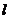 交
交 于点
于点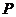 ,求动点
,求动点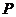 的轨迹方程.
的轨迹方程.
例3.已知椭圆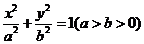 ,
,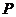 为椭圆上除长轴端点外的任一点,
为椭圆上除长轴端点外的任一点,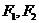 为椭圆的两个焦点,(1)若
为椭圆的两个焦点,(1)若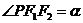 ,
,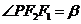 ,求证:离心率
,求证:离心率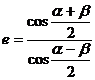 ;
;
(2)若 ,求证:
,求证: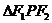 的面积为
的面积为 .
.
例4设椭圆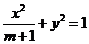 的两个焦点是
的两个焦点是 ,且椭圆上存在点
,且椭圆上存在点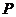 ,使得直线
,使得直线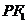 与直线
与直线 垂直.(1)求实数
垂直.(1)求实数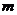 的取值范围;(2)设
的取值范围;(2)设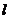 是相应于焦点
是相应于焦点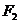 的准线,直线
的准线,直线 与
与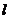 相交于点
相交于点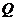 ,若
,若 ,求直线
,求直线 的方程.
的方程.
例5(05上海)点A、B分别是椭圆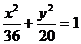 长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于
长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于 轴上方,
轴上方, 。
。
(1)求点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于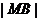 ,求椭圆上的点到点M的距离
,求椭圆上的点到点M的距离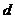 的最小值。
的最小值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com