1.　　　 In this_____(地区)，most students go to school no foot.

2. 两人一组复习第一课时所学的对话

·平行训练·

1. 以小组为单位背诵单词。

3.　 学习合理 安排行程，并合理选用交通工具。

[学习流程]　 一·自学指导·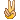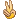

2.　　　 熟练掌握谈论交通方式和距离的句型。

1.　　　 巩固本单元单词。

12.已知函数y=f(x)对任意x,y∈R均有f(x)+f(y)=f(x+y),且当x＞0时，f(x)＜0,f(1)=- .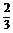　

(1)判断并证明f(x)在R上的单调性；　

(2)求f(x)在［-3，3］上的最值.　

解 (1)f(x)在R上是单调递减函数　

证明如下：　

令x=y=0,f(0)=0,令x=-y可得：f(-x)=-f(x),在R上任取x₁＜x₂,则x₂-x₁＞0,　

∴f(x₂)-f(x₁)=f(x₂)+f(-x₁)=f(x₂-x₁).又∵x＞0时，f(x)＜0,　

∴f(x₂-x₁)＜0,即f(x₂)＜f(x₁).由定义可知f(x)在R上为单调递减函数.　

(2)∵f(x)在R上是减函数，　

∴f(x)在［-3，3］上也是减函数.　

∴f(-3)最大，f(3)最小.f(3)=f(2)+f(1)=f(1)+f(1)+f(1)=3×(-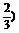=-2.　

∴f(-3)=-f(3)=2.即f(x)在［-3，3］上最大值为2，最小值为-2.

11.已知f(x)=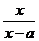(x≠a).　

(1)若a=-2,试证f(x)在(-∞,-2)内单调递增；　

(2)若a＞0且f(x)在(1,+∞)内单调递减，求a的取值范围.　

(1)证明 　任设x₁＜x₂＜-2,则f(x₁)-f(x₂)=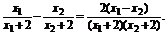　

∵(x₁+2)(x₂+2)＞0,x₁-x₂＜0,∴f(x₁)＜f(x₂),∴f(x)在(-∞,-2)内单调递增.　

(2)解 　任设1＜x₁＜x₂,则　f(x₁)-f(x₂)=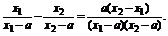　

∵a＞0,x₂-x₁＞0,∴要使f(x₁)-f(x₂)＞0,只需(x₁-a)(x₂-a)＞0恒成立，

∴a≤1.综上所述知0＜a≤1.

10.函数f(x)对任意的实数m、n有f(m+n)=f(m)+f(n),且当x＞0时有f(x)＞0.　

(1)求证：f(x)在(-∞,+∞)上为增函数；　

(2)若f(1)=1,解不等式f［log₂(x²-x-2)］＜2.　

(1)证明 　设x₂＞x₁,则x₂-x₁＞0.　

∵f(x₂)-f(x₁)=f(x₂-x₁+x₁)-f(x₁)=f(x₂-x₁)+f(x₁)-f(x₁)=f(x₂-x₁)＞0,

∴f(x₂)＞f(x₁),f(x)在(-∞,+∞)上为增函数.　

(2)解　 ∵f(1)=1,∴2=1+1=f(1)+f(1)=f(2). 　

又f［log₂(x²-x-2)］＜2,∴f［log₂(x²-x-2)］＜f(2).　

∴log₂(x²-x-2)＜2,于是∴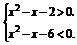

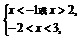
即-2＜x＜-1或2＜x＜3.∴原不等式的解集为{x|-2＜x＜-1或2＜x＜3}.

9.已知f(x)在定义域(0，+∞)上为增函数，且满足f(xy)=f(x)+f(y),f(3)=1,试解不等式f(x)+f(x-8)≤2.

解 　根据题意，由f(3)=1,得f(9)=f(3)+f(3)=2.　

又f(x)+f(x-8)=f［x(x-8)］,故f［x(x-8)］≤f(9).　

∵f(x)在定义域(0,+∞)上为增函数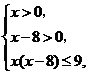，∴解得8＜x≤9.