8.已知下列四个命题：①若f(x)为减函数，则-f(x)为增函数；②若f(x)为增函数，则函数g(x)=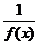在其定义域内为减函数；③若f(x)与g(x)均为(a,b)上的增函数，则f(x)·g(x)也是区间(a,b)上的增函数；④若f(x)与g(x)在(a,b)上分别是递增与递减函数，且g(x)≠0，则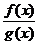在(a,b)上是递增函数.其中命题正确的是　　　　 (填序号)

答案　 ①　

7.已知y=f(x)是定义在(-2，2)上的增函数，若f(m-1)＜f(1-2m)，则m的取值范围是　　　　　　　 .　

答案　 (-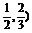

6.若函数f(x)=(m-1)x²+mx+3 (x∈R)是偶函数，则f(x)的单调减区间是　　　 .　

答案　 ［0，+∞)

5.已知f(x)=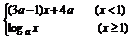是(-∞,+∞)上的减函数，那么a的取值范围是　 　　　.

答案 ［，)

4.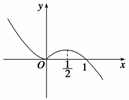函数f(x)(x∈R)的图象如下图所示，则函数g(x)=f(log_ax) (0＜a＜1)的单调减区间是　　　　 .　　　　

答案 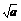［,1］

3.函数y=lg(x²+2x+m)的值域是R,则m的取值范围是　　　　 .　

答案　 m≤1

2.已知函数f(x)在区间［a，b］上单调，且f(a)·f(b)＜0，则下列对方程f(x)=0在区间［a，b］上根的分布情况的判断有误的是　　　　 (填序号).

　 ①至少有一实根　　　　　　　　　　　　　　　　　　 ②至多有一实根

③没有实根　　　　　　　　　　 　　　　　　　　　　　④必有惟一的实根

　答案　 ①③

1.函数f(x)=ln(4+3x-x²)的单调递减区间是　　　　　 .

答案 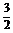［，4)　

14.设a,b,c∈R⁺且a+b+c=1，试求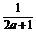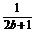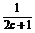：++的最小值.

解　 ∵a+b+c=1，a、b、c为正数，

∴(2a+1+2b+1+2c+1)

≥(1+1+1)²,

∴++≥.

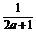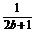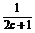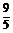当且仅当2a+1=2b+1=2c+1，即a=b=c时“=”成立，

∴当a=b=c=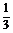时，

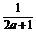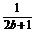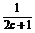++取最小值.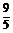

13.(2008·南京第二次调研)已知f(x)=,a≠b,

求证：|f(a)-f(b)|＜|a-b|.

证明　 方法一　 ∵f(a)=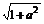,f(b)= ,

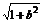∴原不等式化为|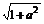-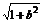|＜|a-b|.

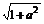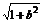∵|-|≥0，|a-b|≥0，

∴要证|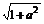-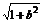|＜|a-b|成立,

只需证(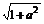-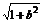)²＜(a-b)².

即证1+a²+1+b²-2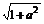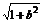＜a²-2ab+b²,

即证2+a²+b²-2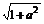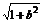＜a²-2ab+b².

只需证2+2ab＜2，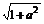

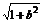即证1+ab＜.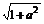

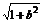当1+ab＜0时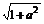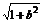，∵＞0,

∴不等式1+ab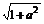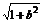＜成立.

从而原不等式成立.

当1+ab≥0时，要证1+ab＜,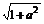

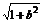只需证(1+ab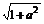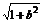)²＜()²,

即证1+2ab+a²b²＜1+a²+b²+a²b²,即证2ab＜a²+b².

∵a≠b,∴不等式2ab＜a²+b²成立.∴原不等式成立.

方法二　 ∵|f(a)-f(b)|=|-|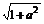

==，

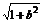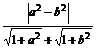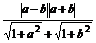又∵|a+b|≤|a|+|b|=+＜+，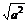

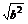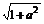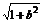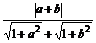∴＜1.

∵a≠b,∴|a-b|＞0.∴|f(a)-f(b)|＜|a-b|.