
3、2008年9月,中国爆发三鹿婴幼儿奶粉受污染事件,导致食用了受污染奶粉的婴幼儿产生肾结石病症,其原因也是奶粉中含有三聚氰胺。三聚氰胺性状为纯白色单斜棱晶体,分子式C3N6H6 [C3N3(NH2)3],无味,密度为1.573 g/cm3 (16 ℃)。常压熔点354 ℃(分解);快速加热升华,升华温度300 ℃。溶于热水,微溶于冷水,极微溶于热乙醇,不溶于醚、苯和四氯化碳,可溶于甲醇、甲醛、乙酸、热乙二醇、甘油、吡啶等。低毒。在一般情况下较稳定,但在高温下可能会分解放出氰化物。三聚氰胺呈弱碱性,与盐酸、硫酸、硝酸、乙酸、草酸等都能形成三聚氰胺盐。 请根据以上信息,回答下列问题:
(1)、下列描述属于三聚氰胺的化学性质的是:( )
A、三聚氰胺性状为纯白色单斜棱晶体,无味 B、快速加热升华,升华温度300 ℃
C、溶于热水,微溶于冷水,极微溶于热乙醇
D、在一般情况下较稳定,但在高温下可能会分解放出氰化物
(2)、三聚氰胺分子式为C3N6H6,相对子质量是_____,其含氮的质量分数为_________.
三聚氰胺也被人称为“蛋白精”,价格便宜。 牛奶和奶粉添加三聚氰胺,主要是因为它能冒充蛋白质。试解释三聚氰胺可以冒充蛋白质的原因_______________________。
(3)、三聚氰胺目前较多采用以尿素硅胶为催化剂,在380-400 ℃温度下沸腾反应,并进一步缩合生成三聚氰胺,同时得到氨气和二氧化碳。试写出反应的方程式:___________________________ .
2、在“三鹿”奶粉事件之前,关于奶粉在有些地区曾发生“毒奶粉”事件。劣质奶粉制造商为牟取暴利,大大降低了奶粉中蛋白质的含量,导致食用这种奶粉的众多婴幼儿严重营养不良乃至死亡。为了测定某牛奶样品中蛋白质的含量,现采用“盖尔达法”分解其中的蛋白质。其原理是把蛋白质中的氮元素完全转化为氨气(化学式为NH3),再用稀硫酸吸收氨气,反应的化学方程式为:2 NH3+H2SO4= (NH4)2 SO4,现取该奶粉样品100g,用“盖尔达法”分解其中的蛋白质,产生的氨气用7.5g溶质质量分数为19.6%的稀硫酸恰好完全吸收。
计算并回答下列问题:
(1)产生氨气的质量是多少?(计算结果精确到0.01,下同)
(2)含氮元素的质量多少?
(3)该奶粉中氮的含量是否达到了国家规定的标准。(奶粉中蛋白质的含量国家标准为:每100g婴幼儿奶粉中含12g~25g。蛋白质含氮元素的质量分数为16%)
1、在手足口病患病儿的护理中,专家指出注意口腔皮肤清洁,每天用生理盐水清洁口腔。生理盐水是指浓度为 的NaCl溶液。要配置1000克这样的溶液需要NaCl 克,水 毫升。
20.(本小题共13分)
已知数集 具有性质
具有性质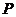 ;对任意的
;对任意的
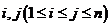 ,
,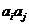 与
与 两数中至少有一个属于
两数中至少有一个属于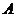 .
.
(Ⅰ)分别判断数集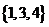 与
与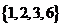 是否具有性质
是否具有性质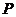 ,并说明理由;
,并说明理由;
(Ⅱ)证明: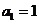 ,且
,且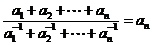 ;
;
(Ⅲ)证明:当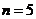 时,
时,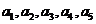 成等比数列..
成等比数列.. 
[解析]本题主要考查集合、等比数列的性质,考查运算能力、推理论证能力、分
分类讨论等数学思想方法.本题是数列与不等式的综合题,属于较难层次题.
(Ⅰ)由于 与
与 均不属于数集
均不属于数集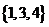 ,∴该数集不具有性质P.
,∴该数集不具有性质P.
由于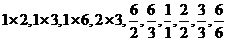 都属于数集
都属于数集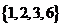 ,
,
∴该数集具有性质P.
(Ⅱ)∵ 具有性质P,∴
具有性质P,∴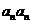 与
与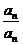 中至少有一个属于A,
中至少有一个属于A,
由于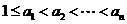 ,∴
,∴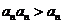 ,故
,故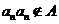 .
.
从而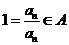 ,∴
,∴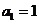 .
.
∵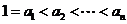 , ∴
, ∴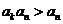 ,故
,故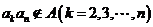 .
.
由A具有性质P可知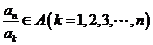 .
.
又∵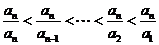 ,
,
∴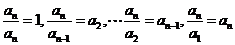 ,
,
从而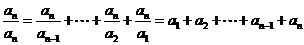 ,
,
∴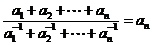 .
.
(Ⅲ)由(Ⅱ)知,当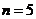 时,有
时,有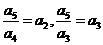 ,即
,即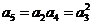 ,
,
∵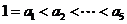 ,∴
,∴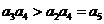 ,∴
,∴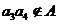 ,
,
由A具有性质P可知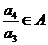 .
.
由 ,得
,得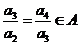 ,且
,且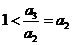 ,∴
,∴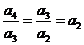 ,
,
∴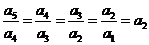 ,即
,即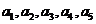 是首项为1,公比为
是首项为1,公比为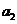 成等比数列..k.s.5.
成等比数列..k.s.5.
19.(本小题共14分)
已知双曲线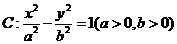 的离心率为
的离心率为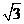 ,右准线方程为
,右准线方程为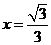
(Ⅰ)求双曲线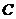 的方程;
的方程;
(Ⅱ)设直线 是圆
是圆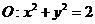 上动点
上动点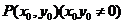 处的切线,
处的切线, 与双曲线
与双曲线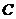 交
交
于不同的两点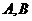 ,证明
,证明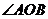 的大小为定值..
的大小为定值..
[解法1]本题主要考查双曲线的标准方程、圆的切线方程等基础知识,考查曲线和方程
的关系等解析几何的基本思想方法,考查推理、运算能力.
(Ⅰ)由题意,得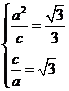 ,解得
,解得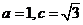 ,
,
∴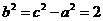 ,∴所求双曲线
,∴所求双曲线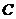 的方程为
的方程为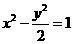 .
.
(Ⅱ)点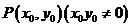 在圆
在圆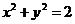 上,
上,
圆在点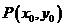 处的切线方程为
处的切线方程为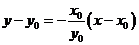 ,
,
化简得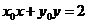 .
.
由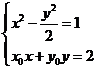 及
及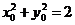 得
得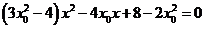 ,
,
∵切线 与双曲线C交于不同的两点A、B,且
与双曲线C交于不同的两点A、B,且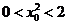 ,
,
∴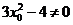 ,且
,且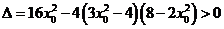 ,
, 
设A、B两点的坐标分别为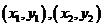 ,
,
则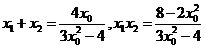 ,
,
∵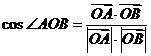 ,且
,且
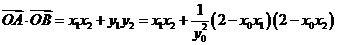 ,
,
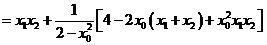
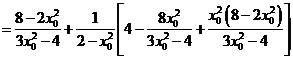
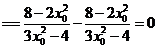 .
.
∴ 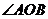 的大小为
的大小为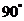 ..
..
[解法2](Ⅰ)同解法1.
(Ⅱ)点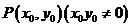 在圆
在圆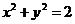 上,
上,
圆在点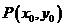 处的切线方程为
处的切线方程为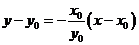 ,
,
化简得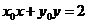 .由
.由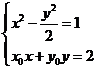 及
及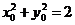 得
得
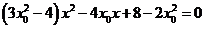 ①
①
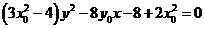 ②
②
∵切线 与双曲线C交于不同的两点A、B,且
与双曲线C交于不同的两点A、B,且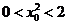 ,
,
∴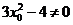 ,设A、B两点的坐标分别为
,设A、B两点的坐标分别为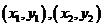 ,
,
则 ,
,
∴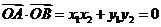 ,∴
,∴ 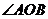 的大小为
的大小为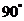 .
.
(∵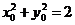 且
且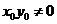 ,∴
,∴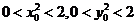 ,从而当
,从而当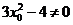 时,方程①和方程②的判别式均大于零).
时,方程①和方程②的判别式均大于零).
18.(本小题共13分)
设函数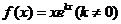
(Ⅰ)求曲线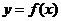 在点
在点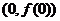 处的切线方程;
处的切线方程;
(Ⅱ)求函数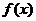 的单调区间;
的单调区间;
(Ⅲ)若函数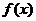 在区间
在区间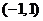 内单调递增,求
内单调递增,求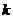 的取值范围.
的取值范围.
[解析]本题主要考查利用导数研究函数的单调性和极值、解不等式等基础知识,考查综合分析和解决问题的能力.
(Ⅰ)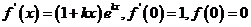 ,
,
曲线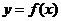 在点
在点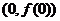 处的切线方程为
处的切线方程为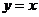 .
.
(Ⅱ)由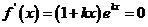 ,得
,得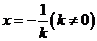 ,
,
若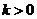 ,则当
,则当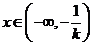 时,
时,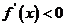 ,函数
,函数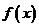 单调递减,
单调递减,
当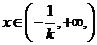 时,
时,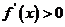 ,函数
,函数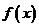 单调递增,
单调递增, 

若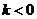 ,则当
,则当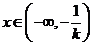 时,
时,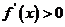 ,函数
,函数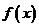 单调递增,
单调递增,
当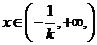 时,
时,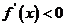 ,函数
,函数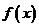 单调递减,
单调递减, 
(Ⅲ)由(Ⅱ)知,若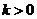 ,则当且仅当
,则当且仅当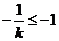 ,
,
即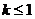 时,函数
时,函数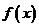
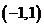 内单调递增,
内单调递增,
若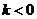 ,则当且仅当
,则当且仅当 ,
,
即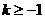 时,函数
时,函数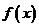
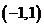 内单调递增,
内单调递增,
综上可知,函数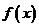
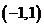 内单调递增时,
内单调递增时,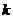 的取值范围是
的取值范围是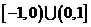 .
.
17.(本小题共13分)
某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是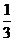 ,遇到红灯时停留的时间都是2min.
,遇到红灯时停留的时间都是2min.
(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(Ⅱ)求这名学生在上学路上因遇到红灯停留的总时间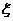 的分布列及期望.
的分布列及期望.
[解析]本题主要考查随机事件、互斥事件、相互独立事件等概率知识、考查离散型随机变量的分布列和期望等基础知识,考查运用概率与统计知识解决实际问题的能力.
(Ⅰ)设这名学生在上学路上到第三个路口时首次遇到红灯为事件A,因为事件A等于事件“这名学生在第一和第二个路口没有遇到红灯,在第三个路口遇到红灯”,所以事件A的概率为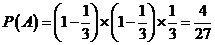 .
.
(Ⅱ)由题意,可得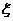 可能取的值为0,2,4,6,8(单位:min).
可能取的值为0,2,4,6,8(单位:min). 
事件“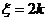 ”等价于事件“该学生在路上遇到
”等价于事件“该学生在路上遇到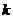 次红灯”(
次红灯”( 0,1,2,3,4),
0,1,2,3,4),
∴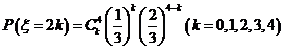 ,
, 
∴即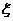 的分布列是
的分布列是
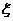 |
0 |
2 |
4 |
6 |
8 |
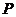 |
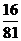 |
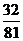 |
 |
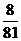 |
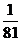 |
∴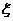 的期望是
的期望是 .
.
16.(本小题共14分)
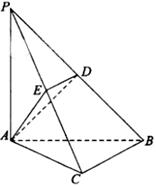
如图,在三棱锥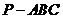 中,
中,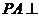 底面
底面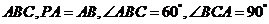 ,
,
点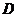 ,
,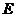 分别在棱
分别在棱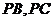 上,且
上,且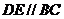
(Ⅰ)求证: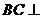 平面
平面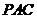 ;
;
(Ⅱ)当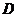 为
为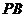 的中点时,求
的中点时,求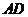 与平面
与平面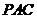 所成的角的大小;
所成的角的大小;
(Ⅲ)是否存在点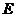 使得二面角
使得二面角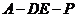 为直二面角?并说明理由.
为直二面角?并说明理由.
[解法1]本题主要考查直线和平面垂直、直线与平面所成的角、二面角等基础知识,考查空间想象能力、运算能力和推理论证能力.
 (Ⅰ)∵PA⊥底面ABC,∴PA⊥BC.
(Ⅰ)∵PA⊥底面ABC,∴PA⊥BC.
又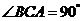 ,∴AC⊥BC.
,∴AC⊥BC.
∴BC⊥平面PAC.
(Ⅱ)∵D为PB的中点,DE//BC,
∴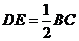 ,
,
又由(Ⅰ)知,BC⊥平面PAC,
∴DE⊥平面PAC,垂足为点E.
∴∠DAE是AD与平面PAC所成的角,
∵PA⊥底面ABC,∴PA⊥AB,又PA=AB,
∴△ABP为等腰直角三角形,∴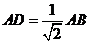 ,
,
∴在Rt△ABC中,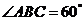 ,∴
,∴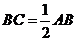 .
.
∴在Rt△ADE中,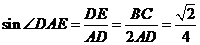 ,
,
∴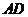 与平面
与平面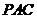 所成的角的大小
所成的角的大小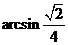 .
.
(Ⅲ)∵AE//BC,又由(Ⅰ)知,BC⊥平面PAC,∴DE⊥平面PAC,
又∵AE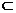 平面PAC,PE
平面PAC,PE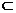 平面PAC,∴DE⊥AE,DE⊥PE,
平面PAC,∴DE⊥AE,DE⊥PE,
∴∠AEP为二面角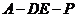 的平面角,
的平面角,
∵PA⊥底面ABC,∴PA⊥AC,∴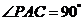 .
.

∴在棱PC上存在一点E,使得AE⊥PC,这时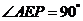 ,
,
故存在点E使得二面角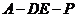 是直二面角.
是直二面角.
[解法2]如图,以A为原煤点建立空间直角坐标系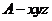 ,
,
设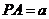 ,由已知可得
,由已知可得
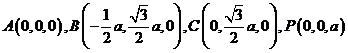 .
.
(Ⅰ)∵ ,
,
∴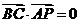 ,∴BC⊥AP.
,∴BC⊥AP.
又∵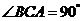 ,∴BC⊥AC,∴BC⊥平面PAC.
,∴BC⊥AC,∴BC⊥平面PAC.
(Ⅱ)∵D为PB的中点,DE//BC,∴E为PC的中点,
∴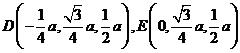 ,
,
∴又由(Ⅰ)知,BC⊥平面PAC,∴∴DE⊥平面PAC,垂足为点E.
∴∠DAE是AD与平面PAC所成的角,
∵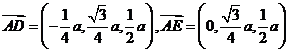 ,
,
∴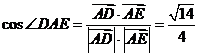 .
.
∴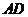 与平面
与平面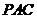 所成的角的大小
所成的角的大小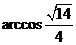 .
.
(Ⅲ)同解法1.
15.(本小题共13分)
在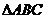 中,角
中,角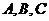 的对边分别为
的对边分别为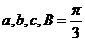 ,
,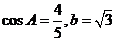 .
.
(Ⅰ)求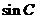 的值;
的值;
(Ⅱ)求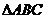 的面积.
的面积.
[解析]本题主要考查三角形中的三角函数变换及求值、诱导公式、三角形的面积公式等基础知识,主要考查基本运算能力.
(Ⅰ)∵A、B、C为△ABC的内角,且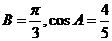 ,
,
∴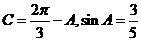 ,
,
∴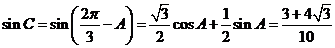 .
.
(Ⅱ)由(Ⅰ)知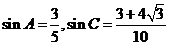 ,
,
又∵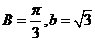 ,∴在△ABC中,由正弦定理,得
,∴在△ABC中,由正弦定理,得
∴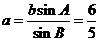 .
.
∴△ABC的面积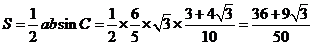 .
.
14.已知数列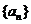 满足:
满足: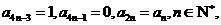 则
则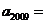 ________;
________;
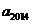 =_________.
=_________.
[答案]1,0
[解析]本题主要考查周期数列等基础知识.属于创新题型.
依题意,得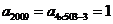 ,
,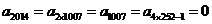 .
.
∴应填1,0.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com