
5.(北京卷7)过直线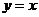 上的一点作圆
上的一点作圆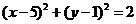 的两条切线
的两条切线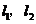 ,当直线
,当直线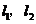 关于
关于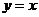 对称时,它们之间的夹角为
对称时,它们之间的夹角为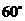
4.(北京卷5)若实数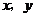 满足
满足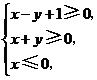 则
则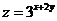 的最小值是1
的最小值是1
3.(全国二11)等腰三角形两腰所在直线的方程分别为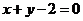 与
与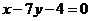 ,原点在等腰三角形的底边上,则底边所在直线的斜率为3
,原点在等腰三角形的底边上,则底边所在直线的斜率为3
2.(全国二5)设变量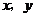 满足约束条件:
满足约束条件: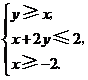 ,则
,则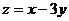 的最小值-8
的最小值-8
13.解决直线与圆的关系问题时,要充分发挥圆的平面几何性质的作用(如半径、半弦长、弦心距构成直角三角形,切线长定理、割线定理、弦切角定理等等)!
已知圆满足:①截y轴所得弦长为2;②被x轴分成两段圆弧,其弧长的比为3∶1,③圆心到直线l:x-2y=0的距离为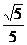 ,求该圆的方程.
,求该圆的方程.
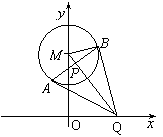 如图,已知⊙M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别切⊙M于A,B两点,⑴如果
如图,已知⊙M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别切⊙M于A,B两点,⑴如果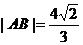 ,求直线MQ的方程;
,求直线MQ的方程;
⑵求动弦AB的中点P的轨迹方程.
⑴解(1)由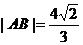 可得
可得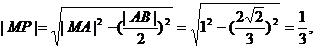 由射影定理得
由射影定理得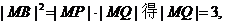 在Rt△MOQ中,
在Rt△MOQ中,
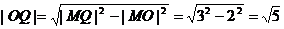 ,
,
故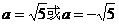 ,所以直线AB方程是
,所以直线AB方程是
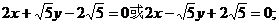
⑵连接MB,MQ,设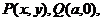 由点M,P,Q在一直线上,得
由点M,P,Q在一直线上,得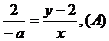
由射影定理得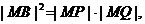 即
即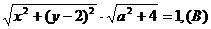
把(A)及(B)消去a,并注意到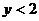 ,可得
,可得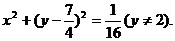
课本题P75练习 2,3;P77练习2,3;P79练习2,3;P80习题 7,8,9;P84练习3,4;P87练习2,3;P87习题4,6,7;P92练习3;P96练习2,3;P96习题14,15,16,17,18 P102练习5,6;习题6,7,9,10 P106练习 3,4,5;P107练习2;P108习题5,6 7,8;
高考题1.(全国一10)若直线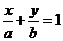 通过点
通过点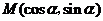 ,则( D
)
,则( D
)
A.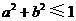 B.
B.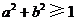 C.
C.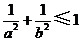 D.
D.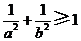
12、圆的切线与弦长:
(1)切线:
①过圆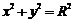 上一点
上一点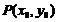 圆的切线方程是:
圆的切线方程是: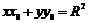 ,
,
过圆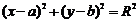 上一点
上一点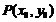 圆的切线方程是:
圆的切线方程是:
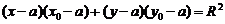 ,
,
一般地,如何求圆的切线方程?(抓住圆心到直线的距离等于半径);
②从圆外一点引圆的切线一定有两条,
设A为圆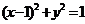 上动点,PA是圆的切线,且|PA|=1,则P点的轨迹方程为________;
上动点,PA是圆的切线,且|PA|=1,则P点的轨迹方程为________;
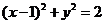 )
)
(2)弦长问题:常用弦心距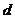 ,弦长一半
,弦长一半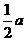 及圆的半径
及圆的半径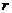 所构成的直角三角形来解:
所构成的直角三角形来解: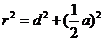 ;
;
11、圆与圆的位置关系(用两圆的圆心距与半径之间的关系判断):已知两圆的圆心分别为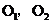 ,半径分别为
,半径分别为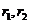 ,则(1)当
,则(1)当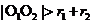 时,两圆外离;(2)当
时,两圆外离;(2)当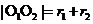 时,两圆外切;(3)当
时,两圆外切;(3)当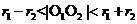 时,两圆相交;(4)当
时,两圆相交;(4)当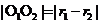 时,两圆内切;(5)当
时,两圆内切;(5)当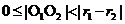 时,两圆内含。
时,两圆内含。
10、直线与圆的位置关系:直线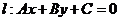 和圆
和圆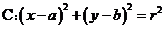
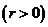 有相交、相离、相切。可从代数和几何两个方面来判断:
有相交、相离、相切。可从代数和几何两个方面来判断:
(1)代数方法(判断直线与圆方程联立所得方程组的解的情况):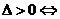 相交;
相交;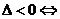 相离;
相离;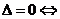 相切;
相切;
(2)几何方法(比较圆心到直线的距离与半径的大小):设圆心到直线的距离为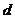 ,则
,则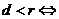 相交;
相交;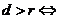 相离;
相离;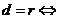 相切。
相切。
提醒:判断直线与圆的位置关系一般用几何方法较简捷。
如(1)圆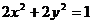 与直线
与直线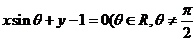
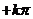 ,
,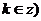 的位置关系为____;相离
的位置关系为____;相离
(2)若直线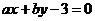 与圆
与圆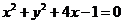 切于点
切于点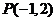 ,则
,则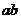 的值__2__;
的值__2__;
(3)直线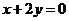 被曲线
被曲线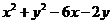
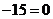 所截得的弦长等于
所截得的弦长等于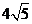 ;
;
(4)一束光线从点A(-1,1)出发经x轴反射到圆C:(x-2)2+(y-3)2=1上的最短路程是 4 ;
(5)已知圆C: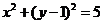 ,直线L:
,直线L: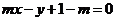 。①求证:对
。①求证:对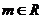 ,直线L与圆C总有两个不同的交点;②设L与圆C交于A、B两点,若
,直线L与圆C总有两个不同的交点;②设L与圆C交于A、B两点,若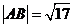 ,求L的倾斜角;③求直线L中,截圆所得的弦最长及最短时的直线方程.
,求L的倾斜角;③求直线L中,截圆所得的弦最长及最短时的直线方程.
②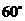 或
或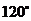 ③最长:
③最长: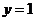 ,最短:
,最短: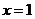
9、点与圆的位置关系:已知点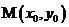 及圆
及圆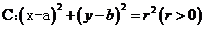 ,(1)点M在圆C外
,(1)点M在圆C外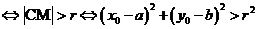 ;(2)点M在圆C内
;(2)点M在圆C内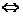
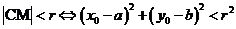 ;(3)点M在圆C上
;(3)点M在圆C上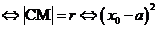
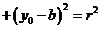 。
。
如点P(5a+1,12a)在圆(x-1)2+y2=1的内部,则a的取值范围是______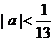
8、圆的方程:
⑴圆的标准方程: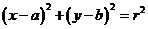 。
。
⑵圆的一般方程: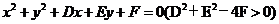 ,
,
特别提醒:只有当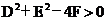 时,方程
时,方程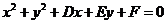 才表示圆心为
才表示圆心为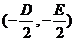 ,半径为
,半径为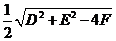 的圆
的圆
(二元二次方程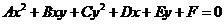 表示圆的充要条件是什么? (
表示圆的充要条件是什么? (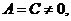 且
且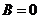 且
且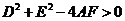 ));
));
(3)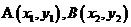 为直径端点的圆方程
为直径端点的圆方程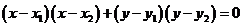
如(1)圆C与圆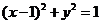 关于直线
关于直线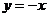 对称,则圆C的方程为
对称,则圆C的方程为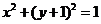 ;
;
(2)圆心在直线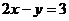 上,且与两坐标轴均相切的圆的标准方程是__________;
上,且与两坐标轴均相切的圆的标准方程是__________;
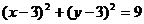 或
或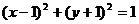
(3)如果直线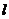 将圆:x2+y2-2x-4y=0平分,且不过第四象限,那么
将圆:x2+y2-2x-4y=0平分,且不过第四象限,那么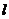 的斜率的取值范围是____;[0,2])
的斜率的取值范围是____;[0,2])
(4)方程x2+y2-x+y+k=0表示一个圆,则实数k的取值范围为____; 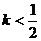
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com