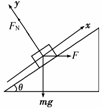
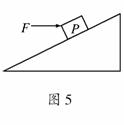
5．如图5所示，位于光滑固定斜面上的小物块P受到一水平向右的推力

F的作用．已知物块P沿斜面加速下滑．现保持F的方向不变，使其

减小，则加速度　　　　　　　　　　　　　　　　　　　 (　)

A．一定变小　　　　　　　　　　　　 B．一定变大

C．一定不变　　　　　　　　　　　　 D．可能变小，可能变大，也可能不变

解析：受力分析如图所示：

沿斜面方向由牛顿第二定律得：

mgsinθ－Fcosθ＝ma.

若F减小，则a增大，所以选B.

答案：B

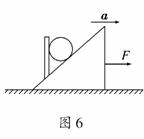　6．如图6所示，质量为m的球置于斜面上，被一个固定在斜面上的竖直

挡板挡住．现用一 个力F拉斜面，使斜面在水平面上做加速度为a的

匀加速直线运动，忽略一切摩擦，以下说法中正确的是　　　 (　)

A．若加速度足够小，竖直挡板对球的弹力可能为零

B．若加速度足够大，斜面对球的弹力可能为零

C．斜面和挡板对球的弹力的合力等于ma

D．斜面对球的弹力不仅有，而且是一个定值

解析：球受力如图，则

F_N2－F_N1sinθ＝ma

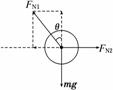F_N1cosθ＝mg

由此判断A、B错误．根据牛顿第二定律，F_N1、F_N2和mg三力

的合力等于ma，C错误．根据F_N1＝，D正确．

答案：D

4．(2010·盐城模拟)在水平地面上运动的小车车厢底部有一质量为m₁的木块，木块和车厢　　

通过一根轻质弹簧相连接，弹簧的劲度系数为k.在车厢的顶部用一根细线悬挂一质量为

m₂的小球．某段时间内发现细线与竖直方向的夹角为θ，在这段时间内木块与车厢保持

相对静止，如图4所示．不计木块与车厢底部的摩擦力，则在这段时间内弹簧的形变为

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

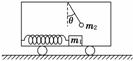
图4

A．伸长量为tanθ　 　　　　　　　　B．压缩量为tanθ

C．伸长量为　 　　　　　　　　　D．压缩量为

解析：分析m₂的受力情况可得：m₂gtanθ＝m₂a，得出：

a＝gtanθ，再对m₁应用牛顿第二定律，得：kx＝m₁a，x＝

tanθ，因a的方向向左，故弹簧处于伸长状态，故A正确．

答案：A

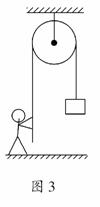
3．(2009·广东高考)建筑工人用图3所示的定滑轮装置运送建筑材料．质量

为70.0 kg的工人站在地面上，通过定滑轮将20.0 kg的建筑材料以0.500

m/s²的加速度拉升，忽略绳子和定滑轮的质量及定滑轮的摩擦，则工人

对地面的压力大小为(g取10 m/s²)　　　　　　　　　　　　　 (　)

A．510 N　 　　　　B．490 N　　　　 C．890 N　　　　 　D．910 N

解析：对建筑材料进行受力分析．根据牛顿第二定律有F－mg＝ma，

得绳子的拉力大小等于F＝210 N，然后再对人受力分析由平衡的知识得

Mg＝F+F_N，得F_N＝490 N，根据牛顿第三定律可知人对地面间的压力为490 N，B对．

答案：B

2．(2008·江苏高考)如图2所示，一质量为M的探空气球在匀速下降，若气球所

受浮力F始终保持不变，气球在运动过程中所受阻力仅与速率有关，重力加

速度为g.现欲使该气球以同样速率匀速上升，则需从气球吊篮中减少的质量

为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．2(M－) 　　　　　B．M－　　　　　 C．2M－ 　　　　　　　D．0

解析：设减少的质量为Δm，匀速下降时：Mg＝F+kv，匀速上升时：Mg－Δmg+kv＝

F，解得Δm＝2(M－)，A正确．

答案：A

1．如图1所示，物块m与车厢后壁间的动摩擦因数为μ，当该车水平向

　　 右加速运动时，m恰好沿车厢后壁匀速下滑，则车的加速度为(　)

A．g　　　B．μg　　　　　　 C.　 　　　　D.μg

解析：设物块m与车厢后壁间的弹力大小为F_N，物块的加速度大小为

a，对物块由牛顿第二定律得F_N＝ma，竖直方向mg－μF_N＝0，两式联立解得a＝，选

项C对．

答案：C

16．(15分)如图16甲所示，水平传送带的长度L＝6 m，皮带轮以速度v顺时针匀速转动，现在一质量为1 kg的小物块(可视为质点)以水平速度v₀从A点滑上传送带，越过B点后做平抛运动，其水平位移为x，保持物块的初速度v₀不变，多次改变皮带轮的速度v依次测量水平位移x，得到如图16乙所示的x－v图象．

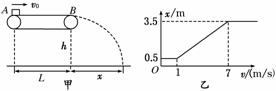
图16

(1)当0＜v≤1 m/s时，物块在A、B之间做什么运动？当v≥7 m/s时，物块在A、B之间做什么运动？

(2)物块的初速度v₀多大？

解析：(1)由于0＜v≤1 m/s时传送带速度增加而物体的平抛初速度不变，所以物体在A、

B之间做匀减速直线运动．

由于v≥7 m/s时传送带速度增加而物体的平抛初速度不变，所以物体在A、B之间做

匀加速直线运动．

(2)由图象可知在传送带速度v_带＝1 m/s时，物体做匀减速运动．

则平抛初速度为v₁＝1 m/s，由动能定理得：

－μmgL＝mv₁²－mv₀²

在v_带＝7 m/s时，物体做匀加速运动，

则平抛初速度为v₂＝7 m/s，由动能定理得：

μmgL＝mv₂²－mv₀²

解得v₀＝ ＝5 m/s.

答案：(1)匀减速直线运动　匀加速直线运动　(2)5 m/s

15．(10分)(2009·浙江高考)某校物理兴趣小组决定举行遥控赛车比赛．比赛路径如图15所示，赛车从起点A出发，沿水平直线轨道运动L后，由B点进入半径为R的光滑竖直圆轨道，离开竖直圆轨道后继续在光滑平直轨道上运动到C点，并能越过壕沟．已知赛车质量m＝0.1 kg，通电后以额定功率P＝1.5 W工作，进入竖直轨道前受到阻力恒为0.3 N，随后在运动中受到的阻力均可不计．图中L＝10.00 m，R＝0.32 m，h＝1.25 m，x＝1.50 m．问：要使赛车完成比赛，电动机至少工作多长时间？(取g＝10 m/s²)

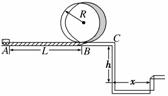
图15

解析：设赛车越过壕沟需要的最小速度为v₁，由平抛运动的规律x＝v₁t

h＝gt²

解得v₁＝x＝3 m/s

设赛车恰好通过圆轨道，对应圆轨道最高点的速度为v₂，最低点的速度为v₃，由牛顿第二定律及机械能守恒定律

mg＝m

mv₃²＝mv₂²+mg(2R)

解得

v₃＝＝4 m/s

通过分析比较，赛车要完成比赛，在进入圆轨道前的速度最小应该是

v_min＝4 m/s

设电动机工作时间至少为t，根据功能关系

Pt－F_fL＝mv_min²

由此可得t＝2.53 s.

答案：2.53 s

对全过程由动能定理得：

mgsinθ·x_AB－μmgcosθ·(2x+x_AB)＝0　　　　　　　　　　　　　　　　　　　　 ②

由①②得：x_AB＝.

答案：

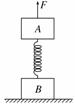
14．(12分) (2010·连云港模拟)一劲度系数k＝800 N/m的轻质弹簧两端分别连接着质量均为12 kg的物体A、B，将它们竖直静止放在水平面上，如图14所示．现将一竖直向上的变力F作用在A上，使A开始向上做匀加速运动，经0.40 s物体B刚要离开地面．g＝10.0 m/s²，试求：

(1)物体B刚要离开地面时，A物体的速度v_A；　　　　　　　　　　　　　　 图14

(2)物体A重力势能的改变量；

(3)弹簧的弹性势能公式：E_p＝kx²，x为弹簧的形变量，则此过程中拉力F做的功为多少？

解析：(1)开始时m_Ag＝kx₁

当物体B刚要离地面时kx₂＝m_Bg

可得：x₁＝x₂＝0.15 m

由x₁+x₂＝at²

v_A＝at

得：v_A＝1.5 m/s.

(2)物体A重力势能增大，

ΔE_pA＝m_Ag(x₁+x₂)＝36 J.

(3)因开始时弹簧的压缩量与末时刻弹簧的伸长量相等，对应弹性势能相等，由功能关系可得：

W_F＝ΔE_pA+m_Av_A²＝49.5 J.

答案：(1)1.5 m/s　(2)36 J　(3)49.5 J

13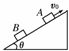．(10分)如图13所示，质量为m的物体从倾角为θ的斜面上的A点以速度v₀

沿斜面上滑，由于μmgcosθ＜mgsinθ，所以它滑到最高点后又滑下来，当它下

滑到B点时，速度大小恰好也是v₀，设物体与斜面间的动摩擦因数为μ，求

AB间的距离．　　　　　　　　　　　　　　　　　　　　　　　 　　　　　图13

解析：设物体m从A点到最高点的位移为x，对此过程由动能定理得：

12．(9分)某兴趣小组为测一遥控电动小车的额定功率，进行了如下实验：

①用天平测出电动小车的质量为0.4 kg；

②将电动小车、纸带和打点计时器按如图11所示安装；

图11

③接通打点计时器(其打点周期为0.02 s)；

④使电动小车以额定功率加速运动，达到最大速度一段时间后关闭小车电源．待小车　　

静止时再关闭打点计时器(设在整个过程中小车所受的阻力恒定)．

在上述过程中，打点计时器在纸带上所打的点迹如图12甲、乙所示，图中O点是打点

计时器打的第一个点．

图12

请你分析纸带数据，回答下列问题：

(1)该电动小车运动的最大速度为________m/s；

(2)该电动小车运动过程中所受的阻力大小为________ N；

(3)该电动小车的额定功率为________W.

解析：(1)速度恒定时

v＝＝ m/s＝1.50 m/s.

(2)匀减速运动阶段

a＝≈－4.00 m/s²

F_f＝ma＝－1.60 N

(3)F＝－F_f

电动小车的额定功率

P＝Fv＝1.60×1.50 W＝2.40 W.

答案：(1)1.50　(2)1.60　(3)2.40