
5、氨水作为反应物时写成NH3·H2O;作为生成物时,若在加热条件下或溶液浓度过大时可写成NH3↑,否则一般写成NH3·H2O。如氢氧化钠溶液与氯化铵溶液混合不加热则为NH4++OH-=NH3·H2O,若加热则为NH4++OH- NH3↑+H2O
NH3↑+H2O
4、微溶物作为反应物,若是澄清溶液则用离子符号表示,若是浊液则用化学式表示。微溶物作为生成物时,一般用化学式表示,并标“↓”。如澄清石灰水中通入适量二氧化碳:Ca2++2OH-+CO2=CaCO3↓+H2O; 向石灰乳中加入过量碳酸钠溶液:Ca(OH)2+CO32-=CaCO3↓+2OH-。
3、明确那些物质能改写离子形式。凡是溶于水的强电解质在溶液中可改写成离子形式,即弱酸、弱碱、不溶物、单质、氧化物、气体均不能改写成离子符号。这要求熟记常见酸碱盐的溶解性,可总结为“钾钠铵硝盐易溶,盐酸盐中银不溶,硫酸盐中钡不溶,溶碱仅有钾钠钡”,同时还应了解中学阶段中常见的弱酸(碳酸、硅酸、亚硫酸、次氯酸、氢氟酸、氢硫酸、羧酸等)、弱碱(氨水)溶液。再就是注意酸式盐的特殊性,强酸的酸式盐中氢可改写成氢离子,弱酸的酸式盐氢不能改写成氢离子,如:硫酸氢钠溶液与氢氧化钡溶液: 2H++SO42-+Ba2++2OH-=BaSO4↓+2H2O,碳酸氢钠溶液与氢氧化钠溶液作用:HCO3-+OH-=CO32-+H2O
2、尊重客观事实。化学反应确实能够发生的才行,不能想当然地乱写。如铁与盐酸反应生成氯化亚铁而不是氯化铁;铁与铁的化合物与硝酸反应时首先生成+3价铁离子,待硝酸反应结束后+3价铁离子再与铁反应生成+2价铁离子。
1、判断反应是否为离子反应。通常认为在溶液中有电解质参与的反应为离子反应,只有这样的离子反应才能写出离子方程式,否则不能书写离子方程式。如高锰酸钾固体受热分解、加热消石灰与氯化铵的固体混合物等反应就不能写出离子方程式。
离子方程式的书写通常有两种方法,其一是传统的根据化学方程式来书写:即“一写二拆三删四查”步骤,其中“写”是保证,“拆”是关键。具体为:①写出正确的化学方程式,②把溶于水的强电解质改写成离子符号,③删去方程式两边相同的(不参加反应的)离子,④检查方程式两边的电荷及原子种类与个数是否守恒。其二是从反应实质角度来书写,具体为①分析溶液中含有那些离子,②分析那些离子能发生反应,③分析离子的来源,若来自强电解质时则直接写成离子,若来自于弱电解质时则写成弱电解质的化学式,④写出离子方程式并注意原子与电荷守恒即可。第一种方法通常用于与量多少无关的反应的离子方程式书写,第二种方法比较使用于与量有关的反应的离子方程式书写。如碳酸氢钙溶液与氢氧化钙溶液混合反应时,可以出现碳酸氢钙溶液过量,也可以出现氢氧化钙溶液过量,这两种情况的产物并不一致,故使用第一种方法书写时则难度很大,此时若使用第二种方法较易,具体如下:两溶液中共含有HCO3-、Ca2+、OH-,其中HCO3-与OH-反应生成的CO32-还能够Ca2+反应再生成CaCO3沉淀,所以当碳酸氢钙溶液过量时,则应以氢氧化钙溶液完全反应为研究对象讨论,不难写出Ca2++2OH-+2HCO3-=CaCO3+CO32-+2H2O;当氢氧化钙溶液过量时则应以碳酸氢钙溶液完全反应为研究对象讨论,不难写出Ca2++HCO3-+OH-=CaCO3+CO32-+H2O。
9.(2006全国I)如图,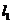 、
、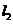 是互相垂直的异面直线,MN是它们的公垂线段
是互相垂直的异面直线,MN是它们的公垂线段 点A、B在
点A、B在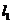 上,C在
上,C在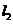 上,
上,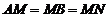

(Ⅰ)证明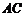 ⊥
⊥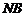 ;
;
(Ⅱ)若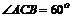 ,求
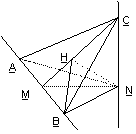
,求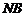 与平面ABC所成角的余弦值
与平面ABC所成角的余弦值
证明 (Ⅰ)由已知l2⊥MN, l2⊥l1 , MN∩l1 =M, 可得l2⊥平面ABN 由已知MN⊥l1 , AM=MB=MN,可知AN=NB且AN⊥NB
由已知MN⊥l1 , AM=MB=MN,可知AN=NB且AN⊥NB
又AN为AC在平面ABN内的射影 ∴AC⊥NB
∴AC⊥NB
(Ⅱ)∵Rt△CAN≌Rt△CNB,
∴AC=BC,又已知∠ACB=600,
因此△ABC为正三角形.
∵Rt△ANB≌Rt△CNB,
∴NC=NA=NB,因此N在平面ABC内的射影H是正三角形ABC的中心,连结BH,∠NBH为NB与平面ABC所成的角 在Rt△NHB中,
在Rt△NHB中,
cos∠NBH= = = 
[探索题]
如图,在600的二面角α-CD-β中,AC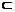 α,BD
α,BD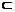 β,且ACD=450,tg∠BDC=2,CD=a,AC=
β,且ACD=450,tg∠BDC=2,CD=a,AC=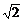 x,BD=
x,BD=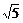 x,当x为何值时,A、B的距离最小?并求此距离.
x,当x为何值时,A、B的距离最小?并求此距离.
解析:
作AE⊥CD于E,BF⊥CD于F,则EF为异面直线AE、BF的公垂段,AE与BF成600角,可求得|AB|=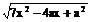 ,当x=
,当x=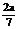 时,|AB|有最小值
时,|AB|有最小值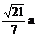 .
.
8. (2004广东)如图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2。E、F分别是线段AB、BC上的点,且EB=BF=1。求直线EC1与FD1所成的角的余弦值。
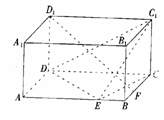
解:延长BA至点E1,使AE1=1,连结E1F、DE1、D1E1、DF,有 D1C1//E1E, D1C1=E1E,则四边形D1E1EC1是平行四边形。则E1D1//EC1.于是∠E1D1F为直线
D1C1//E1E, D1C1=E1E,则四边形D1E1EC1是平行四边形。则E1D1//EC1.于是∠E1D1F为直线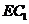 与
与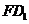 所成的角。
所成的角。
在Rt△BE1F中,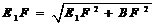 .
.
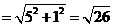 . 在Rt△D1DE1中,
. 在Rt△D1DE1中, 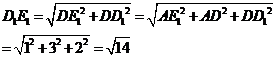
在Rt△D1DF中,
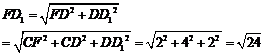
在△E1FD1中,由余弦定理得:
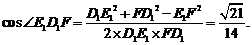
∴直线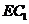 与
与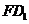 所成的角的余弦值为
所成的角的余弦值为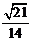 .
.
7.已知正方体ABCD-A1B1C1D1的边长为a,E、F分别是棱A1B1、CD的中点.
(1)证明:截面C1EAF⊥平面ABC1.
(2)求点B到截面C1EAF的距离.
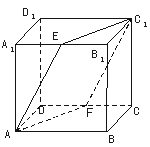
证明(1):连结EF、AC1和BC1,易知四边形EB1CF是平行四边形,从而EF∥B1C,直线B1C⊥BC1且B1C⊥AB,则直线B1C⊥平面ABC1,得EF⊥平面ABC1.而EF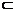 平面C1EAF,得平面C1EAF⊥平面ABC1.
平面C1EAF,得平面C1EAF⊥平面ABC1.
解(2):在平面ABC1内,过B作BH,使BH⊥AC1,H为垂足,则BH的长就是点B到平面C1EAF的距离,在直角三角形中,BH=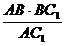 =
=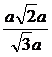 =
=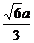 .
.
6.已知l1、l2是两条异面直线,α、β、γ是三个平面依次互相平行,l1、l2分别交α、β、γ于A、B、C和D、E、F,AB=4,BC=12,DF=10,又l1与α成30°角,则β与γ的距离是__________;DE=__________.
◆答案: 1-4.DAAB;
5. 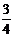 ; 6. 6 、 2.5;
; 6. 6 、 2.5;
[解答题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com