
7.(2006陕西文、理)已知非零向量与满足(+)·=0且·= ,则△ABC为( )
A.三边均不相等的三角形 B.直角三角形 C.等腰非等边三角形 D.等边三角形
6、(2008海南、宁夏文)已知平面向量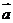 =(1,-3),
=(1,-3),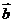 =(4,-2),
=(4,-2),
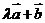 与
与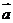 垂直,则
垂直,则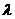 是( )
是( )
A. -1 B. 1 C. -2 D. 2
5.(2006四川文、理)如图, 已知正六边形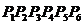 ,下列向量的数量积中最大的是( )
,下列向量的数量积中最大的是( )
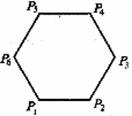 (A)
(A)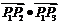 (B)
(B)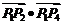 (C)
(C)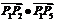 (D)
(D)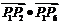
4.(2004全国卷Ⅱ文)已知向量a、b满足:|a|=1,|b|=2,|a-b|=2,则|a+b|=( )
(A)1 (B)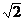 (C)
(C)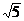 (D)
(D)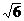
3.(2005全国卷Ⅱ理、文)已知点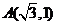 ,
,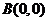 ,
,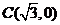 .设
.设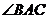 的平分线
的平分线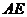
与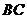 相交于
相交于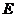 ,那么有
,那么有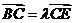 ,其中
,其中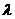 等于( )
等于( )
(A)2 (B)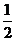 (C)-3 (D)-
(C)-3 (D)-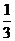
2.(2001江西、山西、天津理)若向量a=(1,1),b=(1,-1),c=(-1,2),则c= ( )
(A)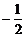 a+
a+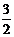 b (B)
b (B)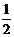 a-
a-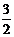 b (C)
b (C)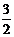 a
a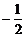 b (D)-
b (D)-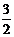 a
a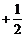 b
b
1.(2008广东文)已知平面向量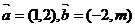 ,且
,且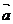 ∥
∥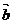 ,则
,则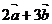 =( )
=( )
A.(-2,-4) B. (-3,-6) C. (-4,-8) D. (-5,-10)
16、解:(1)记”所取出的非空子集满足性质r”为事件A
基本事件总数n=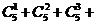
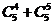 =31
=31
事件A包含的基本事件是{1,4,5}、{2,3,5}、{1,2,3,4}
事件A包含的基本事件数m=3
所以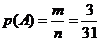
(II)依题意, 的所有可能取值为1,2,3,4,5
的所有可能取值为1,2,3,4,5
又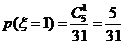 ,
, 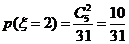 ,
, 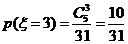
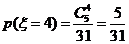 ,
, 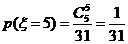
故 的分布列为:
的分布列为:
 |
1 |
2 |
3 |
4 |
5 |
|
P |
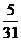 |
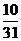 |
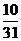 |
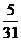 |
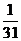 |
从而E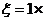
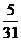 +2
+2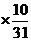 +3
+3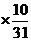 +4
+4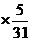 +5
+5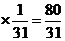
18、(福建卷)16.(13分)
从集合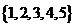 的所有非空子集中,等可能地取出一个。
的所有非空子集中,等可能地取出一个。
(1) 记性质r:集合中的所有元素之和为10,求所取出的非空子集满足性质r的概率;
(2)
记所取出的非空子集的元素个数为 ,求
,求 的分布列和数学期望E
的分布列和数学期望E
17、(湖南卷)17.(本小题满分12分)
为拉动经济增长,某市决定新建一批重点工程,分别为基础设施工程、民生工程和产业建设工程三类,这三类工程所含项目的个数分别占总数的.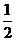 、
、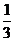 、
、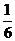 ,现在3名工人独立地从中任选一个项目参与建设。
,现在3名工人独立地从中任选一个项目参与建设。 

(I)求他们选择的项目所属类别互不相同的概率;
(II)记 为3人中选择的项目属于基础设施工程、民生工程和产业建设工程的人数,求
为3人中选择的项目属于基础设施工程、民生工程和产业建设工程的人数,求 的分布列及数学期望。
的分布列及数学期望。
解:记第1名工人选择的项目属于基础设施工程、民生工程和产业建设工程分别为事件 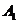 ,
,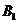 ,
,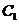 ,i=1,2,3.由题意知
,i=1,2,3.由题意知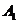
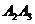 相互独立,
相互独立,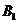
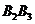 相互独立,
相互独立,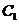
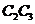 相互独立,
相互独立,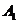 ,
,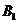 ,
,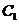 (i,j,k=1,2,3,且i,j,k互不相同)相互独立,且P(
(i,j,k=1,2,3,且i,j,k互不相同)相互独立,且P(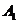 )=,P(
)=,P(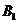 )=
)=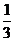 ,P(
,P(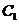 )=
)=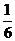
(1) 他们选择的项目所属类别互不相同的概率
P=3!P(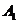
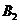
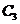 )=6P(
)=6P(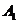 )P(
)P(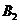 )P(
)P(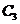 )=6
)=6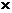
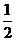
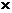
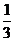
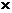
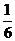 =
=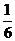
(2) 解法1 设3名工人中选择的项目属于民生工程的人数为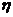 ,由己已知,
,由己已知,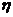 -B(3,
-B(3,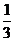 ),且
),且 =3
=3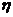 。
。
所以P( =0)=P(
=0)=P(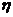 =3)=
=3)=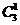
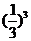 =
=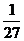 ,
,
P( =1)=P(
=1)=P(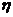 =2)=
=2)= 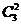
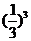
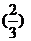 =
= 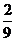


P( =2)=P(
=2)=P(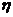 =1)=
=1)=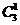
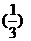
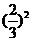 =
=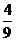
P( =3)=P(
=3)=P(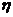 =0)=
=0)= 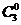
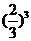 =
= 
故 的分布是
的分布是
 |
0 |
1 |
2 |
3 |
|
P |
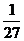 |
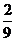 |
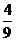 |
 |
 的数学期望E
的数学期望E =0
=0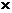
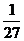 +1
+1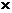
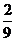 +2
+2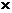
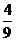 +3
+3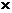
 =2
=2
解法2 第i名工人选择的项目属于基础工程或产业工程分别为事件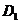 ,
,
i=1,2,3 ,由此已知,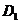 ·D,
·D,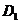 相互独立,且
相互独立,且
P(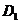 )-(
)-(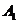 ,
,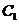 )= P(
)= P(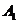 )+P(
)+P(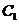 )=
)=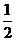 +
+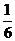 =
=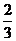
所以 --
--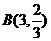 ,既
,既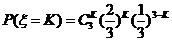 ,
,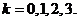


故 的分布列是
的分布列是
 |
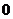 |
1 |
2 |
3 |
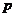 |
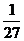 |
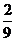 |
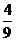 |
 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com