
 等差数列的概念、性质及基本公式。
等差数列的概念、性质及基本公式。 等比数列的概念、性质及基本公式。
等比数列的概念、性质及基本公式。
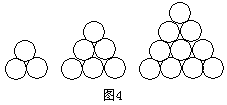
 (
(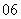 广东)在德国不莱梅举行的第
广东)在德国不莱梅举行的第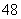 届世乒赛期 间,某商场橱窗里用同样的乒乓球堆成若干准“正三棱锥”形的展品,其中第
届世乒赛期 间,某商场橱窗里用同样的乒乓球堆成若干准“正三棱锥”形的展品,其中第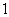 堆只有一层,就一个乒乓球;第
堆只有一层,就一个乒乓球;第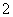 、
、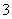 、
、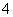 、…堆最底层(第一层)分别按图
、…堆最底层(第一层)分别按图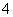 所示方式固定摆放.从第一层开始,每层的小球自然垒放在下一层之上,第
所示方式固定摆放.从第一层开始,每层的小球自然垒放在下一层之上,第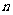 堆第
堆第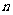 层就放一个乒乓球,以
层就放一个乒乓球,以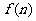 表示第
表示第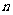 堆的乒乓球总数,则
堆的乒乓球总数,则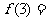 ;
;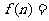
(答案用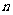 表示).
表示).
 (
(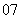 福建)数列
福建)数列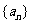 的前
的前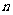 项和为
项和为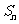 ,若
,若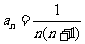 ,则
,则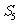 等于
等于
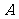
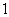
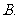
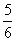
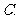
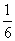
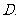
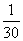
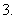 (
(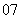 全国Ⅱ)已知数列的通项
全国Ⅱ)已知数列的通项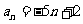 ,其前
,其前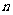 项和为
项和为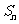 ,则
,则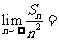
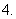 (
( 福建文)“数列
福建文)“数列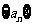 的前
的前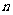 项和为
项和为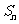 ,
,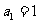 ,
,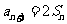
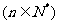 .
.
(Ⅰ)求数列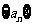 的通项
的通项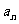 ;
;
(Ⅱ)求数列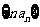 的前
的前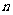 项和
项和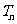 .
.
( 荆州统测)数列
荆州统测)数列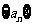 满足递推关系:
满足递推关系: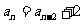 ,且
,且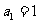 ,
,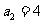 .
.
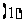 求
求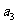 、
、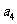 ;
;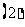 求
求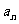 ;
;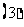 求数列
求数列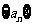 的前
的前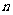 项和.
项和.
 (
(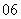 北京)设
北京)设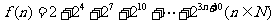 ,则
,则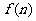 等于
等于
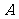
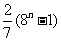
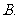
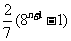
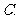
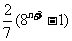
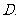
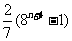
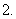 明朝程大拉作数学诗:“远望巍巍塔七层,红光点点加倍增,共灯三百八十一,请问尖头 盏灯”.
明朝程大拉作数学诗:“远望巍巍塔七层,红光点点加倍增,共灯三百八十一,请问尖头 盏灯”.
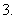 求数列
求数列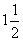 ,
,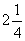 ,
,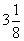 ,
,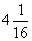 ,…的前
,…的前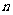 项和.
项和.
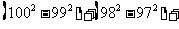 …
…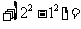
 在数列
在数列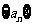 中,
中,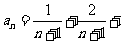 …
…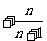 ,又
,又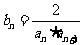 ,则数列
,则数列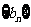 的前
的前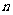 项和为
项和为
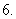 求数列
求数列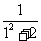 ,
,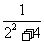 ,
,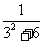 ,
,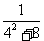 ,…的前
,…的前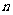 项和
项和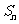 .
.
问题1.求下列数列前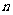 项和:
项和: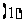
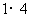 ,
,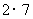 ,
,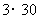 ,…,
,…,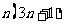 ;
;
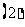
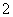 ,
,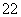 ,
,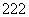 ,…,
,…,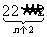 ;
;
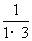 ,
,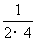 ,
,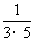 ,…,
,…,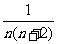 ;
;
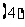
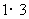 ,
,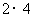 ,
,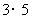 ,…,
,…,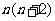 ,
,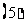
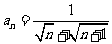 ;
;
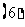
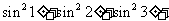 …
…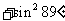 ;
;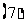
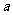 ,
,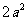 ,
,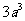 ,…,
,…,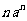 ;
;
问题2.求和
 ;
;
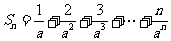 ;
; 
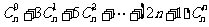
问题3.已知数列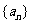 的通项
的通项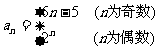 ,求其前
,求其前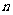 项和
项和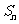
问题4.(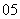 全国Ⅰ文)设正项等比数列
全国Ⅰ文)设正项等比数列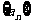 的首项
的首项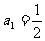 ,前
,前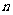 项和为
项和为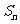 ,且
,且 .(Ⅰ)求
.(Ⅰ)求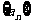 的通项;(Ⅱ)求
的通项;(Ⅱ)求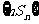 的前
的前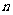 项和
项和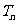 .
.
问题5.(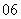 湖北)已知二次函数
湖北)已知二次函数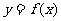 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为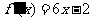 ,数列
,数列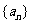 的前
的前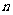 项和为
项和为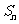 ,点
,点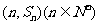 均在函数
均在函数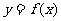 的图像上.(Ⅰ)求数列
的图像上.(Ⅰ)求数列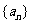 的通项公式;(Ⅱ)设
的通项公式;(Ⅱ)设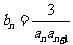 ,
,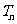 是数列
是数列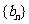 的前
的前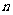 项和,求使得
项和,求使得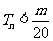 对所有
对所有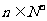 都成立的最小正整数
都成立的最小正整数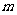 ;
;
 基本公式法:
基本公式法: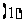 等差数列求和公式:
等差数列求和公式: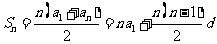
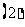 等比数列求和公式:
等比数列求和公式: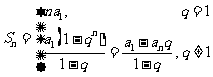
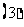
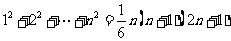 ;
;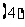
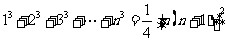 ;
; 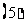
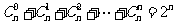 .
.
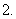 错位相消法:给
错位相消法:给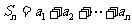 各边同乘以一个适当的数或式,然后把所得的等式和原等式相减,对应项相互抵消,最后得出前
各边同乘以一个适当的数或式,然后把所得的等式和原等式相减,对应项相互抵消,最后得出前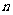 项和
项和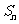 .
.
一般适应于数列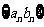 的前
的前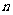 向求和,其中
向求和,其中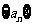 成等差数列,
成等差数列, 成等比数列。
成等比数列。
 分组求和:把一个数列分成几个可以直接求和的数列,然后利用公式法求和。
分组求和:把一个数列分成几个可以直接求和的数列,然后利用公式法求和。
 拆项(裂项)求和:把一个数列的通项公式分成两项差的形式,相加过程中消去中间项,只剩下有限项再求和.
拆项(裂项)求和:把一个数列的通项公式分成两项差的形式,相加过程中消去中间项,只剩下有限项再求和.
常见的拆项公式有:
 若
若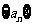 是公差为
是公差为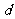 的等差数列,则
的等差数列,则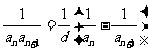 ;
;
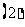
 ;
;
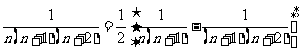 ;
;
 ;
;
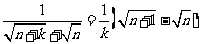 ;
;
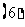
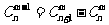 ;
;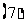
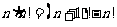 ;
;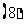
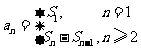
 倒序相加法:根据有些数列的特点,将其倒写后与原数列相加,以达到求和的目的。
倒序相加法:根据有些数列的特点,将其倒写后与原数列相加,以达到求和的目的。
 导数法:灵活利用求导法则有时也可以完成数列求和问题的解答.
导数法:灵活利用求导法则有时也可以完成数列求和问题的解答.
 递推法.
递推法. 奇偶分析法.
奇偶分析法.
 等差数列与等比数列的求和公式的应用;
等差数列与等比数列的求和公式的应用;
 倒序相加、错位相减,分组求和、拆项求和等求和方法;
倒序相加、错位相减,分组求和、拆项求和等求和方法;
 (
(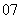 陕西)各项均为正数的等比数列
陕西)各项均为正数的等比数列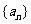 的前
的前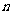 项和为
项和为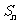 为,若
为,若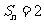 ,
,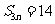 ,
,
则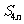 等于
等于 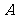
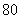
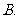
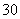
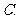
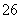
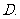
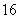
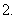 (
(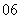 辽宁)在等比数列
辽宁)在等比数列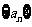 中,
中,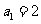 ,前
,前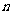 项和为
项和为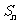 ,若数列
,若数列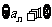 也是等比数列,则
也是等比数列,则
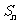 等于
等于
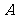
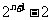
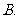
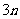
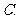
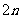
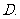
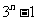
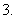 (
(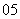 湖北)设等比数列
湖北)设等比数列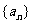 的公比为
的公比为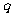 ,前
,前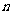 项和为
项和为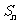 ,若
,若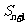 ,
,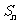 ,
,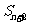 成等差数列,则
成等差数列,则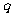 的值为
的值为
 (
( 全国文Ⅱ)设等比数列
全国文Ⅱ)设等比数列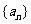 的公比
的公比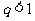 ,前
,前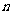 项和为
项和为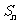 .已知
.已知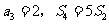 ,
,
求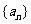 的通项公式.
的通项公式.
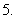 (
( 北京)数列
北京)数列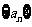 中,
中,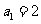
 (
(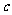 是常数,
是常数,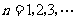 ),且
),且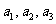
成公比不为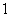 的等比数列.(Ⅰ)求
的等比数列.(Ⅰ)求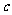 的值;(Ⅱ)求
的值;(Ⅱ)求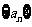 的通项公式.
的通项公式.
 (
( 山东)设数列
山东)设数列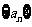 满足
满足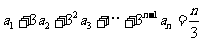 ,
,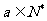 .
.
(Ⅰ)求数列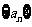 的通项;(Ⅱ)设
的通项;(Ⅱ)设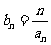 ,求数列
,求数列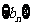 的前
的前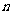 项和
项和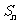 .
.
 (
( 福建文)已知数列
福建文)已知数列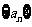 满足
满足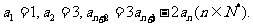
(Ⅰ)证明:数列 是等比数列;
是等比数列;
(Ⅱ)求数列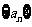 的通项公式;
的通项公式;
(Ⅲ)若数列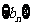 满足
满足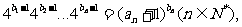 证明
证明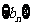 是等差数列。
是等差数列。
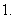 (
( 湖南文)在等比数列
湖南文)在等比数列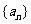 (
(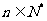 )中,若
)中,若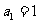 ,
,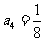 ,则该数列的前
,则该数列的前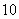 项和为
项和为 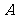
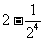
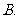
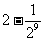
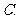
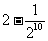
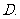
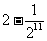
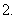 (
(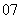 海南文)已知
海南文)已知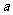 、
、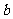 、
、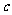 、
、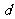 成等比数列,且曲线
成等比数列,且曲线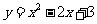 的顶点是
的顶点是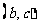 ,
,
则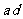 等于
等于 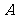
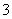
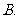
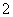
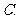

 (
(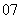 重庆)设
重庆)设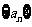 为公比
为公比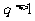 的等比数列,若
的等比数列,若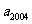 和
和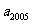 是方程
是方程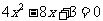 的两根,则
的两根,则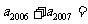 ______.
______.
 (
( 湖北)若数列
湖北)若数列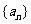 满足
满足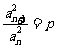 (
(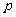 为正常数,
为正常数,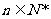 ),则称
),则称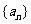 为“等方比数列”.甲:数列
为“等方比数列”.甲:数列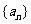 是等方比数列; 乙:数列
是等方比数列; 乙:数列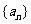 是等比数列,则
是等比数列,则
 甲是乙的充分条件但不是必要条件
甲是乙的充分条件但不是必要条件 甲是乙的必要条件但不是充分条件
甲是乙的必要条件但不是充分条件
 甲是乙的充要条件
甲是乙的充要条件
 甲既不是乙的充分条件也不是乙的必要条件
甲既不是乙的充分条件也不是乙的必要条件
问题1. (
( 全国Ⅰ文)已知
全国Ⅰ文)已知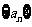 为等比数列,
为等比数列,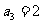 ,
,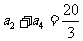 ,求
,求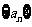 的通项公式;
的通项公式;
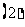 (
(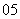 江苏)在等比数列
江苏)在等比数列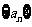 中,
中,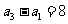 ,
,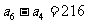 ,
,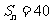 ,求公比
,求公比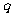 、
、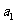 及
及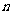
问题2. 已知数列
已知数列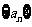 是等比数列,且
是等比数列,且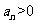 ,
,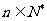 ,
,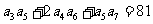 ,
,
则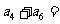
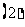 (
(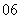 苏州调研)在等比数列
苏州调研)在等比数列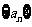 中,
中,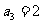 ,
,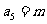 ,
,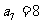 ,则
,则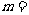
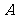
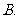
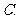

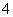
 (
(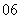 湖北文)在等比数列
湖北文)在等比数列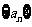 中,
中,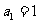 ,
,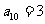 ,则
,则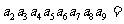
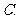
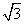
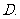
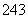
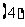 (
(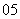 全国Ⅱ文)在
全国Ⅱ文)在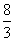 和
和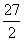 之间插入三个数,使五个数成等比数列,则插入的三个数的乘积是
之间插入三个数,使五个数成等比数列,则插入的三个数的乘积是
 (
( 南京高三期末调研)在等比数列
南京高三期末调研)在等比数列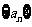 中,已知
中,已知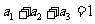 ,
,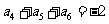 ,
,
则该数列前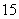 项的和
项的和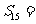
问题3.(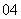 全国Ⅱ)数列
全国Ⅱ)数列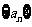 的前
的前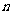 项和记为
项和记为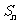 ,已知
,已知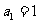 ,
,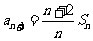 (
(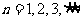 ) 证明:
) 证明: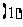 数列
数列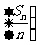 是等比数列,
是等比数列,
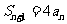
问题4.已知数列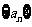 中,
中,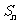 是它的前
是它的前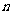 项和,且
项和,且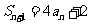
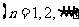 ,
,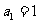 .
.
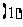 设
设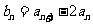
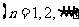 ,求证:数列
,求证:数列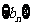 是等比数列;
是等比数列;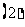 设
设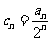
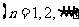 ,
,
求证: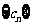 是等差数列;
是等差数列;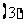 求
求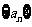 的通项公式
的通项公式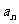 及前
及前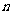 项和公式
项和公式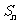
问题5.(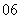 陕西)已知正项数列
陕西)已知正项数列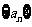 ,其前
,其前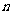 项和
项和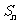 满足
满足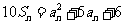 且
且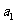 ,
,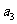 ,
,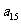 成等比数列,求数列
成等比数列,求数列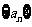 的通项
的通项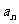
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com