
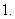 若
若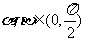 ,且
,且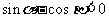 ,则
,则
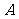
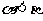
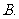
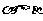
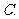
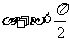
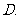
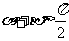
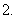 已知
已知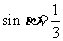 ,
, ,求
,求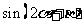 的值.
的值.
 (
( 太原模拟)若
太原模拟)若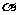 是第三象限角,且
是第三象限角,且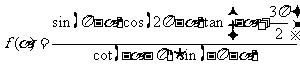
 化简
化简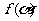 ;
;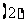 若
若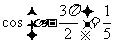 ,求
,求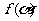 的值;
的值;
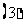 若
若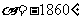 ,求
,求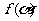 的值
的值
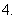 是否存在
是否存在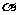 、
、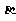 ,
,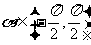 ,
,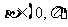 使等式
使等式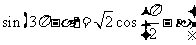 ,
,
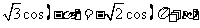 同时成立?若存在,求出
同时成立?若存在,求出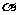 、
、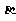 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
问题1. (
(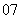 全国Ⅱ文)
全国Ⅱ文)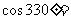
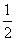
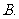
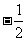
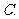
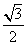
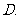
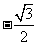
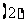 (
( 黄岗模拟)已知
黄岗模拟)已知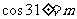 ,则
,则

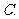
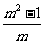
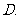
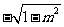
问题2.化简: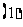
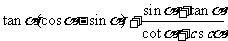
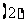
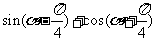
问题3.求值: 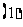 已知
已知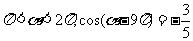 ,求
,求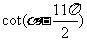 的值;
的值;
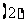 若
若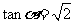 ,求值①
,求值①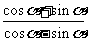 ;②
;②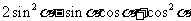 .
.
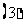 求值
求值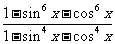 .
.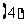 已知:
已知: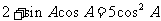 ,求
,求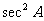 ;
;
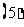 已知:
已知: ,且
,且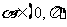 ,求
,求 的值.
的值.
问题4.已知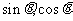 是方程
是方程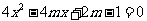 的两个根,
的两个根,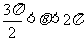 ,求角
,求角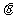 .
.
问题5.求证: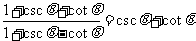
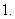 利用平方关系时,要注意开方后符号的选取;
利用平方关系时,要注意开方后符号的选取;
 诱导公式的作用在于将任意角的三角函数转化为
诱导公式的作用在于将任意角的三角函数转化为 内角的三角函数值,其解题思路是化负角为正角,化复杂角为简单角,运用时应充分注意符号;
内角的三角函数值,其解题思路是化负角为正角,化复杂角为简单角,运用时应充分注意符号;
 利用商数关系、倒数关系能够完成切割化弦;
利用商数关系、倒数关系能够完成切割化弦;
 涉及
涉及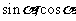 的二次齐次式(如
的二次齐次式(如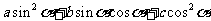 )的问题常采用“
)的问题常采用“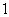 ”代换法求解;
”代换法求解;
 涉及
涉及 的问题常采用平方法求解;
的问题常采用平方法求解;
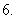 涉及
涉及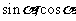 的齐次分式(如
的齐次分式(如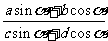 )的问题常采用分式的基本性质进行变形.
)的问题常采用分式的基本性质进行变形.
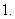 同角三角函数的基本关系式:
同角三角函数的基本关系式:
(1)倒数关系: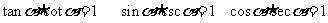 ;
;
(2)商数关系: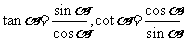 ;
;
(3)平方关系: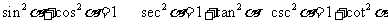 .
.
 诱导公式:奇变偶不变,符号看象限.
诱导公式:奇变偶不变,符号看象限.
 (
( 上海文)三角方程
上海文)三角方程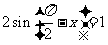 的解集为
的解集为
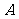
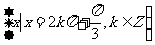
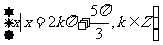
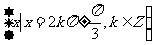 .
. 
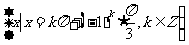
 (
(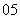 全国Ⅲ)设
全国Ⅲ)设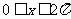 ,且
,且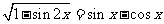 ,则
,则
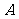
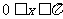
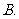
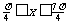
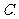
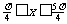
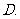
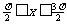
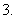 (
(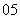 湖北)若
湖北)若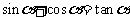
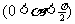 ,则
,则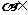
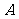
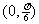
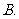
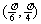
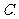
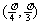
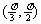
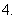 (
( 全国)在
全国)在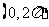 内,使
内,使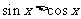 成立的
成立的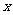 取值范围为
取值范围为
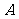
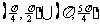
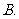
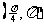
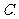
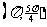
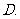
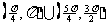
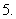 (
(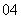 辽宁)若
辽宁)若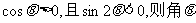 的终边所在象限是
的终边所在象限是
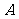 第一象限
第一象限 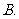 第二象限
第二象限 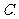 第三象限
第三象限 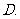 第四象限
第四象限
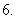 (
(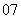 北京)已知
北京)已知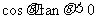 ,那么角
,那么角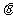 是
是
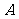 第一或第二象限角
第一或第二象限角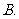 第二或第三象限角
第二或第三象限角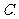 第三或第四象限角
第三或第四象限角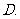 第一或第四象限角
第一或第四象限角
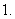 已知
已知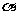 为第三象限的角,则
为第三象限的角,则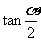
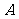 一定是正数
一定是正数 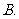 一定是负数
一定是负数 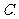 正数、负数都有可能
正数、负数都有可能 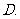 有可能是零
有可能是零
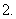 (
(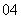 浙江)在
浙江)在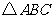 中,“
中,“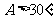 ”是“
”是“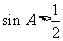 ”的
”的
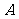 充分而不必要条件
充分而不必要条件 必要而不充分条件
必要而不充分条件 充分必要条件
充分必要条件 既不充分也必要条件
既不充分也必要条件
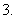 终边与坐标轴重合的角的集合是
终边与坐标轴重合的角的集合是
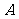
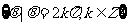
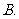
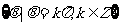 ;
;
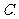
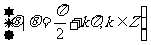 ;
;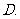
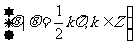
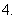
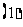 如果
如果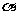 是第一象限的角,那么
是第一象限的角,那么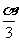 是第几象限的角?
是第几象限的角?
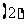 已知
已知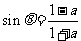 ,
,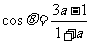 ,若
,若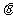 是第二象限角,求实数
是第二象限角,求实数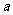 的值.
的值.
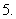 确定下列各式的符号:
确定下列各式的符号: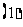
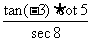 ;
;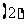
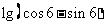
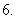 (
(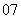 湖南省十校联考)已知
湖南省十校联考)已知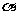 终边上的一点
终边上的一点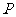 坐标是
坐标是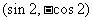 ,则
,则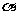 的一个弧度数为
的一个弧度数为 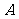

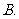
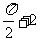
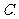
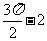
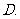
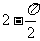
问题1.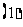 (
( 浙江)点
浙江)点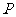 从
从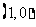 出发,沿单位圆
出发,沿单位圆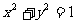 逆时针方向运动
逆时针方向运动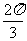 弧长到达
弧长到达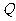 点,则
点,则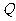 的坐标为
的坐标为
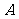
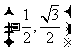
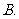
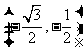
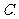
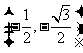
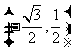
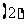 设
设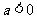 ,角
,角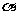 的终边经过点
的终边经过点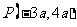 ,那么
,那么 的值等于
的值等于
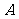
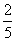
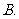
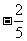
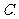
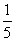
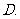
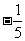
问题2.(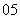 全国Ⅲ)已知
全国Ⅲ)已知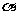 为第三象限角,则
为第三象限角,则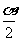 所在的象限是
所在的象限是
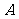 第一或第二象限 ;
第一或第二象限 ;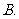 第二或第三象限
第二或第三象限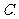 第一或第三象限 ;
第一或第三象限 ;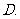 第二或第四象限
第二或第四象限
问题3.求函数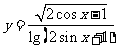 的定义域.
的定义域.
问题4.已知一扇形的中心角为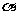 ,所在圆的半径为
,所在圆的半径为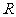 .
. 若
若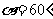 ,
,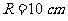 ,求扇形的弧长及该弧所在的弓形的面积;
,求扇形的弧长及该弧所在的弓形的面积;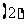 若扇形的周长是一定值
若扇形的周长是一定值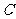
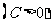 ,当
,当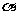 为多少弧度时,该扇形有最大面积?
为多少弧度时,该扇形有最大面积?
 各象限角的三角函数值符号规律:正弦……上为正,下为负,横为零
各象限角的三角函数值符号规律:正弦……上为正,下为负,横为零
余弦……右为正,左为负,纵为零
正切……一三为正,二四为负,横为零,纵不存在
 要正确利用三角函数线解答“三角函数值的大小比较”和“解简单三角不等式”
要正确利用三角函数线解答“三角函数值的大小比较”和“解简单三角不等式”
 三角函数的有界性:
三角函数的有界性: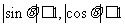 (利用正、余弦函数的有界性可以解决一些值域或最值计算问题)
(利用正、余弦函数的有界性可以解决一些值域或最值计算问题)
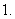 角的概念的推广;象限角、轴线角;与
角的概念的推广;象限角、轴线角;与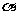 角终边相同的角为
角终边相同的角为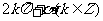 ;
;
 角的度量;角度制、弧度制及其换算关系;弧长公式
角的度量;角度制、弧度制及其换算关系;弧长公式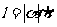 、扇形面积公式
、扇形面积公式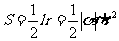 ;
;
 任意角的三角函数,三角函数线的定义.
任意角的三角函数,三角函数线的定义.
(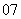 安徽)某国采用养老储备金制度.公民在就业的第一年就交纳养老储备金,数目为
安徽)某国采用养老储备金制度.公民在就业的第一年就交纳养老储备金,数目为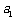 ,以后每年交纳的数目均比上一年增加
,以后每年交纳的数目均比上一年增加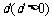 ,因此,历年所交纳的储备金数目
,因此,历年所交纳的储备金数目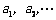 是一个公差为
是一个公差为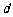 的等差数列.与此同时,国家给予优惠的计息政策,不仅采用固定利率,而且计算复利.这就是说,如果固定年利率为
的等差数列.与此同时,国家给予优惠的计息政策,不仅采用固定利率,而且计算复利.这就是说,如果固定年利率为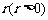 ,那么,在第
,那么,在第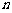 年末,第一年所交纳的储备金就变为
年末,第一年所交纳的储备金就变为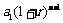 ,第二年所交纳的储备金就变为
,第二年所交纳的储备金就变为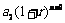 ,
, .以
.以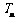 表示到第
表示到第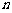 年末所累计的储备金总额.
年末所累计的储备金总额. 写出
写出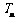 与
与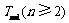 的递推关系式;
的递推关系式;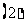 求证:
求证: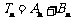 ,其中
,其中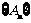 是一个等比数列,
是一个等比数列,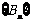 是一个等差数列.
是一个等差数列.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com