
20.
解:(1)由于点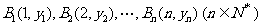 在直线
在直线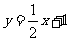 上,
上,
则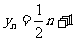 ,
,
因此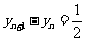 ,所以数列
,所以数列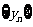 是等差数列
是等差数列
(2)由已知有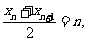 ,那么
,那么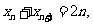 同理
同理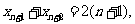
以上两式相减,得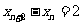 ,
,
∴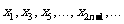 成等差数列;
成等差数列;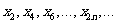 也成等差数列,
也成等差数列,
∴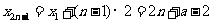 ,
,
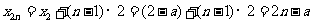
点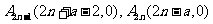 ,则
,则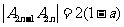 ,
,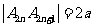 ,
,
而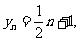
∴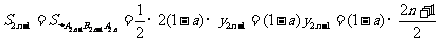
(3)由(1)得: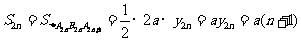 ,
,
则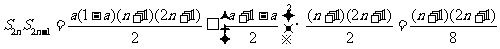
而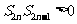 ,则
,则 ,
,
即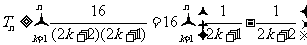
∴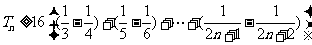
∴
∴
由于
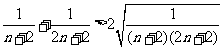 ,
,
而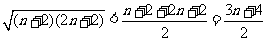 ,
,
则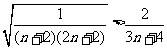 , 从而
, 从而 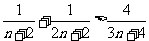 ,
,
同理: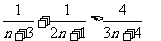
……
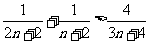
以上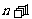 个不等式相加得:
个不等式相加得: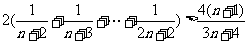
即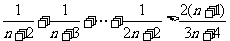 ,
,
从而
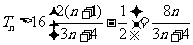 。
。
高级中学2010-2011学年高三第一学期第一次考试
19.
解:(1)设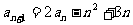 可化为
可化为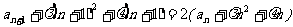 ,
,
即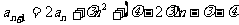 ,故
,故 ,得
,得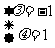 。
。
又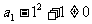 ,所以存在
,所以存在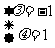 ,使得数列
,使得数列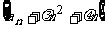 是等比数列。
是等比数列。
(2)由(1)得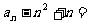
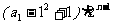 ,得
,得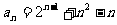 ,所以
,所以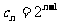 。
。
要使得 成立,
成立,
则有 ,得
,得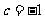 。所以,存在常数
。所以,存在常数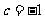 ,使得
,使得 成立。
成立。
(3)证明:因为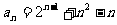 ,所以
,所以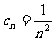 ,而
,而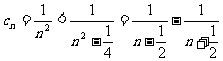 ,
,
所以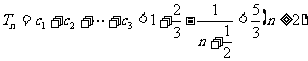 。
。
又当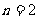 时,
时,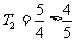 ,符合。
,符合。
当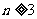 时,
时,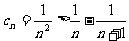 ,
,
得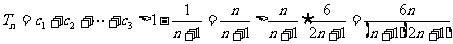 。
。
综上, <
< <
<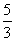
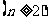 得证。
得证。
18.
解:Q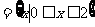 , 对于
, 对于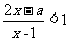 ,当
,当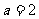 时,P=
时,P=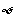 ,符合。
,符合。
当 时,P
时,P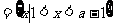 ,此时只需
,此时只需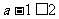 ,即
,即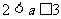 。
。
当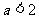 时,P
时,P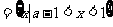 ,此时只需
,此时只需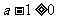 ,即
,即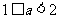 。
。
综上,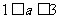 为所求。
为所求。
17.
解:设甲项目投资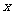 (单位:百万元),乙项目投资
(单位:百万元),乙项目投资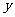 (单位:百万元),两项目增加的
(单位:百万元),两项目增加的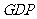 为
为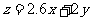 。
。
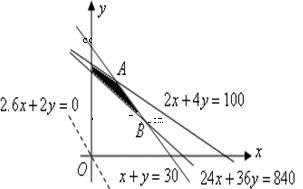
 依题意,
依题意,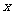 、
、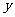 满足
满足 ,所确定的平面区域如图中阴影部分
,所确定的平面区域如图中阴影部分
解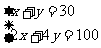 得
得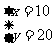 ,
,
解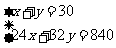 得
得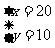
设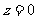 ,得
,得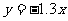 ,将直线
,将直线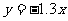 平移至经过点
平移至经过点 ,
,
即甲项目投资2000万元,、乙项目投资1000万元,两项目增加的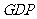 最大
最大
16.
解:(1)由正弦定理有: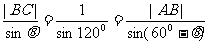 ;
;
∴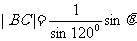 ,
,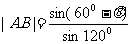 ;
;
∴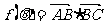
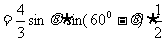
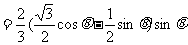
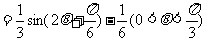
(2)由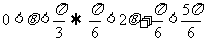 ;
;
∴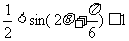 ;∴
;∴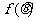
15.
解:(1) 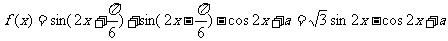
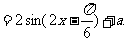 ∴
∴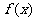 的最小正周期
的最小正周期 .
.
(2) 当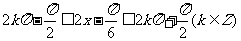 , 即
, 即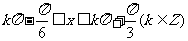 时,函数
时,函数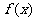 单调递增,故所求区间为
单调递增,故所求区间为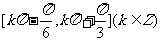
(3)函数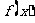 的图像向左平移
的图像向左平移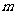
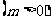 个单位后得
个单位后得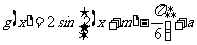 ,
,
要使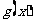 的图像关于y轴对称,只需
的图像关于y轴对称,只需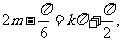
即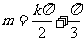 ,所以m的最小值为
,所以m的最小值为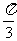 。
。
14. 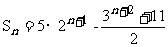
9.
9 10.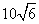 11.
11. 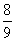 12. 4,12 13.
12. 4,12 13. 
1.A 2A 3.D 4.A 5.B 6.C 7.C 8.A
20.(本小题满分14分)
已知点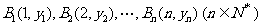 在直线
在直线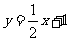 上,点
上,点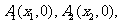
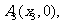 ……,
……,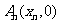 顺次为
顺次为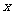 轴上的点,其中
轴上的点,其中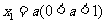 ,对于任意
,对于任意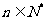 ,点
,点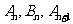 构成以
构成以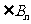 为顶角的等腰三角形, 设
为顶角的等腰三角形, 设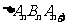 的面积为
的面积为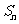 .
.
(1)证明:数列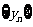 是等差数列;
是等差数列;
(2)求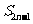 (用
(用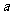 和
和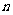 的代数式表示);
的代数式表示);
(3)设数列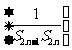 前
前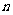 项和为
项和为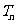 ,判断
,判断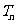 与
与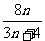 (
(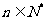 )的大小,并证明你的结论;
)的大小,并证明你的结论;
高级中学2010-2011学年高三第一学期第一次考试
数 学(理)试题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com