
2.证明:
⑴直接证明 ①综合法:一般地,利用已知条件和某些数学定义、定理、公理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法。综合法又叫顺推法或由因导果法。
②分析法:一般地,从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定义、定理、公理等),这种证明的方法叫分析法。分析法又叫逆推证法或执果索因法。
(2)间接证明(反证法):一般地,假设原命题不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明原命题成立,这种证明方法叫反证法。 (理科下转第14页)
2009 年 安 徽 高 考 数 学 常 用 公 式 及 结 论
1.推理:
⑴合情推理:归纳推理和类比推理都是根据已有事实,经过观察、分析、比较、联想,在进行归纳、类比,然后提出猜想的推理,我们把它们称为合情推理。
①归纳推理:由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者由个别事实概括出一般结论的推理,称为归纳推理,简称归纳。
注:归纳推理是由部分到整体,由个别到一般的推理。
②类比推理:由两类对象具有类似和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理,称为类比推理,简称类比。
注:类比推理是特殊到特殊的推理。
⑵演绎推理:从一般的原理出发,推出某个特殊情况下的结论,这种推理叫演绎推理。
注:演绎推理是由一般到特殊的推理。
“三段论”是演绎推理的一般模式,包括:⑴大前提---------已知的一般结论;⑵小前提---------所研究的特殊情况;............ ⑶结论---------根据一般原理,对特殊情况得出的判断。
6.常见结论的否定形式
|
原结论 |
反设词 |
原结论 |
反设词 |
|
是 |
不是 |
至少有一个 |
一个也没有 |
|
都是 |
不都是 |
至多有一个 |
至少有两个 |
|
大于 |
不大于 |
至少有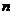 个 个 |
至多有( )个 )个 |
|
小于 |
不小于 |
至多有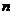 个 个 |
至少有( )个 )个 |
对所有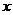 , ,成立 |
存在某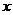 , ,不成立 |
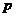 或 或 |
 且 且 |
对任何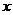 , ,不成立 |
存在某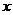 , ,成立 |
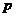 且 且 |
 或 或 |
5.全称量词与存在量词
⑴全称量词-------“所有的”、“任意一个”等,用 表示;
表示;
全称命题p: ; 全称命题p的否定
; 全称命题p的否定 p:
p: 。
。
⑵存在量词--------“存在一个”、“至少有一个”等,用 表示;
表示;
特称命题p: ; 特称命题p的否定
; 特称命题p的否定 p:
p: ;
;
4。四种命题:
⑴原命题:若p则q; ⑵逆命题:若q则p;
⑶否命题:若 p则
p则 q;
⑷逆否命题:若
q;
⑷逆否命题:若 q则
q则 p
p
注:原命题与逆否命题等价;逆命题与否命题等价。
3. 四种命题的相互关系
四种命题的相互关系





原命题 互逆 逆命题



 若p则q 若q则p
若p则q 若q则p

 互 互
互 互
互 为 为 互
否 否
逆 逆





 否 否
否 否
否命题 逆否命题
 若非p则非q 互逆 若非q则非p
若非p则非q 互逆 若非q则非p



2.逻辑联结词:






 ⑴且(and) :命题形式 p
⑴且(and) :命题形式 p q; p q p
q; p q p q p
q p q
q  p
p
 ⑵或(or):
命题形式 p
⑵或(or):
命题形式 p q; 真 真 真 真 假
q; 真 真 真 真 假
 ⑶非(not):命题形式
⑶非(not):命题形式 p .
真
假 假 真 假
p .
真
假 假 真 假
 假 真 假 真 真
假 真 假 真 真
 假 假 假 假 真
假 假 假 假 真
1.充要条件的判断:
(1)定义法----正、反方向推理
注意区分:“甲是乙的充分条件(甲 乙)”与“甲的充分条件是乙(乙
乙)”与“甲的充分条件是乙(乙 甲)”
甲)”
(2)利用集合间的包含关系:例如:若 ,则A是B的充分条件或B是A的必要条件;若A=B,则A是B的充要条件。
,则A是B的充分条件或B是A的必要条件;若A=B,则A是B的充要条件。
2.基本算法语句:





 ⑴输入语句 INPUT “提示内容”;变量
;输出语句:PRINT “提示内容”;表达式
⑴输入语句 INPUT “提示内容”;变量
;输出语句:PRINT “提示内容”;表达式




 赋值语句: 变量=表达式
赋值语句: 变量=表达式
 ⑵条件语句:①
②
⑵条件语句:①
②





 IF 条件THEN
IF条件 THEN
IF 条件THEN
IF条件 THEN
语句体 语句体1
END IF ELSE
 语句体2
语句体2
END IF

⑶循环语句:①当型: ②直到型:





 WHILE条件
DO
WHILE条件
DO
循环体 循环体
WEND LOOP UNTIL 条件


1.程序框图:
⑴图形符号:

 ① 终端框(起止框);②
输入、输出框;
① 终端框(起止框);②
输入、输出框;
 ③
③



 处理框(执行框);④
判断框;⑤ 流程线
;
处理框(执行框);④
判断框;⑤ 流程线
;
⑵程序框图分类:



 ①顺序结构:
②条件结构:
③循环结构:
①顺序结构:
②条件结构:
③循环结构:









 r =0? 否
求n除以i的余数
r =0? 否
求n除以i的余数





 输入n
是
输入n
是










 n不是质数 n是质数
i=i+1
n不是质数 n是质数
i=i+1









 i=2
i=2





 i
i n或r=0?
否
n或r=0?
否
 是
是
注:循环结构分为:Ⅰ.当型(while型) --先判断条件,再执行循环体;
Ⅱ.直到型(until型)--先执行一次循环体,再判断条件。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com