
12.函数零点的求法:
⑴直接法(求 的根);⑵图象法;⑶二分法.
的根);⑵图象法;⑶二分法.
(4)零点定理:若y=f(x)在[a,b]上满足f(a)·f(b)<0 , 则y=f(x)在(a,b)内至少有一个零点。
11.函数图象(曲线)对称性的证明:
(1)证明函数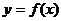 图像的对称性,即证明图像上任意点关于对称中心(对称轴)的对称点仍在图像上;
图像的对称性,即证明图像上任意点关于对称中心(对称轴)的对称点仍在图像上;
(2)证明函数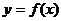 与
与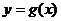 图象的对称性,即证明
图象的对称性,即证明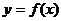 图象上任意点关于对称中心(对称轴)的对称点在
图象上任意点关于对称中心(对称轴)的对称点在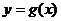 的图象上,反之亦然。
的图象上,反之亦然。
注:①曲线C1:f(x,y)=0关于原点(0,0)的对称曲线C2方程为:f(-x,-y)=0;
曲线C1:f(x,y)=0关于直线x=0的对称曲线C2方程为:f(-x, y)=0;
曲线C1:f(x,y)=0关于直线y=0的对称曲线C2方程为:f(x, -y)=0;
曲线C1:f(x,y)=0关于直线y=x的对称曲线C2方程为:f(y, x)=0
②f(a+x)=f(b-x) (x∈R)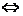 y=f(x)图像关于直线x=
y=f(x)图像关于直线x=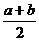 对称;
对称;
特别地:f(a+x)=f(a-x) (x∈R)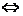 y=f(x)图像关于直线x=a对称.
y=f(x)图像关于直线x=a对称.
③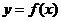 的图象关于点
的图象关于点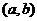 对称
对称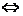
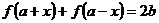 .
.
特别地: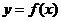 的图象关于点
的图象关于点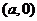 对称
对称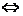
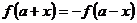 .
.
④函数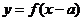 与函数
与函数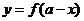 的图象关于直线
的图象关于直线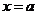 对称;
对称;
函数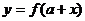 与函数
与函数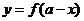 的图象关于直线
的图象关于直线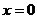 对称。
对称。
10.函数图象:
⑴图象作法 :①描点法 (特别注意三角函数的五点作图)②图象变换法 ③导数法
⑵图象变换:
①
平移变换:ⅰ)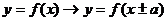 ,
,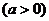 ---左“+”右“-”;
---左“+”右“-”;
ⅱ)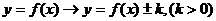 ---上“+”下“-”;
---上“+”下“-”;
②
对称变换:ⅰ)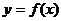
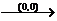
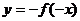 ;ⅱ)
;ⅱ)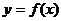
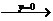
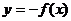 ;
;
ⅲ) 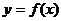
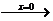
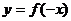 ; ⅳ)
; ⅳ)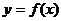
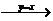
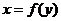 ;
;
③ 翻折变换:
ⅰ) ---(去左翻右)y轴右不动,右向左翻(
---(去左翻右)y轴右不动,右向左翻(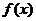 在
在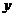 左侧图象去掉);
左侧图象去掉);
ⅱ)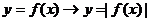 ---(留上翻下)x轴上不动,下向上翻(|
---(留上翻下)x轴上不动,下向上翻(|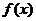 |在
|在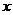 下面无图象);
下面无图象);
9.二次函数:
⑴解析式:①一般式: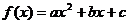 ;②顶点式:
;②顶点式: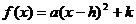 ,
,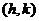 为顶点;
为顶点;
③零点式: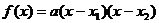 (a≠0).
(a≠0).
⑵二次函数问题解决需考虑的因素:
①开口方向;②对称轴;③端点值;④与坐标轴交点;⑤判别式;⑥两根符号。
二次函数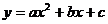 的图象的对称轴方程是
的图象的对称轴方程是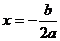 ,顶点坐标是
,顶点坐标是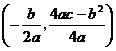 。
。
8.基本初等函数的图像与性质:
㈠.⑴指数函数: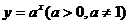 ;⑵对数函数:
;⑵对数函数: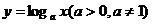 ;
;
⑶幂函数: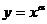 (
(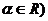 ;⑷正弦函数:
;⑷正弦函数: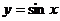 ;⑸余弦函数:
;⑸余弦函数: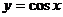 ;
;
(6)正切函数: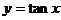 ;⑺一元二次函数:
;⑺一元二次函数: (a≠0);⑻其它常用函数:
(a≠0);⑻其它常用函数:
①
正比例函数: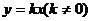 ;②反比例函数:
;②反比例函数: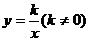 ;③函数
;③函数
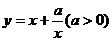
㈡.⑴分数指数幂: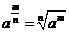 ;
;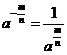 (以上
(以上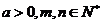 ,且
,且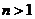 ).
).
⑵.①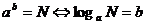 ; ②
; ②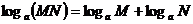 ;
;
③ ; ④
; ④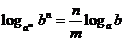 .
.
⑶.对数的换底公式: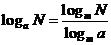 .对数恒等式:
.对数恒等式: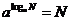 .
.
7.函数的周期性:
(1)周期性的定义:对定义域内的任意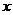 ,若有
,若有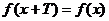 (其中
(其中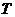 为非零常数),则称函数
为非零常数),则称函数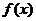 为周期函数,
为周期函数,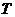 为它的一个周期。所有正周期中最小的称为函数的最小正周期。如没有特别说明,遇到的周期都指最小正周期。
为它的一个周期。所有正周期中最小的称为函数的最小正周期。如没有特别说明,遇到的周期都指最小正周期。
(2)三角函数的周期:①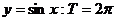 ;②
;②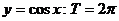 ;③
;③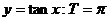 ;
;
④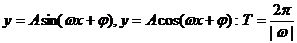 ;⑤
;⑤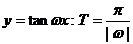
(3)与周期有关的结论:
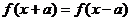 或
或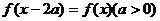
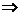
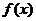 的周期为
的周期为
6.函数的单调性:
⑴单调性的定义:
①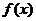 在区间
在区间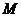 上是增函数
上是增函数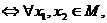 当
当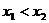 时有
时有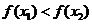 ;
;
②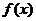 在区间
在区间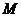 上是减函数
上是减函数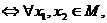 当
当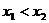 时有
时有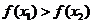 ;
;
⑵单调性的判定:①定义法:一般要将式子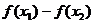 化为几个因式作积或作商的形式,以利于判断符号;②导数法(见导数部分);③复合函数法;④图像法
化为几个因式作积或作商的形式,以利于判断符号;②导数法(见导数部分);③复合函数法;④图像法
注:证明单调性主要用定义法和导数法。
5.函数的奇偶性:
⑴函数的定义域关于原点对称是函数具有奇偶性的必要条件
⑵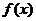 是奇函数
是奇函数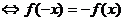 ;
;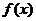 是偶函数
是偶函数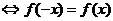 .
.
⑶奇函数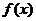 在0处有定义,则
在0处有定义,则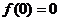
⑷在关于原点对称的单调区间内:奇函数有相同的单调性,偶函数有相反的单调性
⑸若所给函数的解析式较为复杂,应先等价变形,再判断其奇偶性
4.分段函数:值域(最值)、单调性、图象等问题,先分段解决,再下结论。
3.复合函数的有关问题:
(1)复合函数定义域求法:
① 若f(x)的定义域为[a,b],则复合函数f[g(x)]的定义域由不等式a ≤ g(x) ≤ b解出
② 若f[g(x)]的定义域为[a,b],求 f(x)的定义域,相当于x∈[a,b]时,求g(x)的值域.
(2)复合函数单调性的判定:
①首先将原函数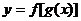 分解为基本函数:内函数
分解为基本函数:内函数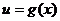 与外函数
与外函数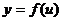
②分别研究内、外函数在各自定义域内的单调性
③根据“同性则增,异性则减”来判断原函数在其定义域内的单调性.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com