
505. 如图9-19,在棱长为a的正方体ABCD-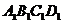 中,O是AC、BD的交点,E、F分别是AB与AD的中点.
中,O是AC、BD的交点,E、F分别是AB与AD的中点.
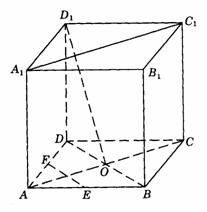
图9-19
(1)求异面直线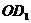 与
与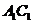 所成角的大小;
所成角的大小;
(2)求异面直线EF与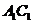 所成角的大小;
所成角的大小;
(3)求异面直线EF与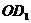 所成角的正切值;
所成角的正切值;
(4)求异面直线EF与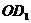 的距离.
的距离.
解析:(1)∵
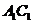 ∥AC,∴
∥AC,∴
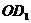 与AC所成的锐角或直角就是
与AC所成的锐角或直角就是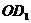 与
与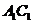 所成的角,连结
所成的角,连结 、
、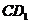 ,在△
,在△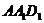 和△
和△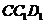 ,∵
,∵ 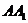 =
=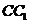 ,
,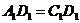 ,
,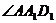
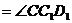
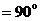 ,∴△
,∴△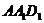 ≌△
≌△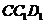 ,∴
,∴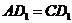 .∴△
.∴△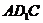 是等腰三角形.∵ O是底边AC的中点,∴
是等腰三角形.∵ O是底边AC的中点,∴
 ,故
,故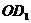 与
与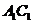 所成的角是90°.
所成的角是90°.
(2)∵ E、F分别是AB、AD中点,∴
EF∥BD,又∵
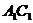 ∥AC,∴
AC与BD所成的锐角或直角就是EF与
∥AC,∴
AC与BD所成的锐角或直角就是EF与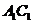 所成的角.∵ 四边形ABCD是正方形,∴
AC⊥BD,∴
EF与
所成的角.∵ 四边形ABCD是正方形,∴
AC⊥BD,∴
EF与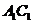 所成的角为90°
所成的角为90°
(3)∵ EF∥BD,∴
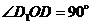 为异面直线EF与
为异面直线EF与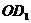 所成的角.∵ 四边形
所成的角.∵ 四边形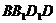 是正方形,∴
是正方形,∴ 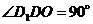 ,∴ 在Rt△
,∴ 在Rt△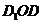 中,
中,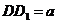 ,
,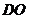 =
=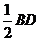 =
=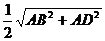
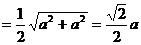 ,∴
,∴ 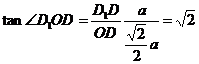 ,即EF与
,即EF与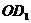 所成角的正切值为
所成角的正切值为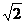 .
.
(4)∵ EF∥BD,BD⊥AC,∴
EF⊥AC,设交点为G.∵ 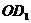 ⊥AC(由(1)
⊥AC(由(1)
知)于O,则AC是异面直线EF与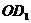 的公垂线,OG的长即为EF与
的公垂线,OG的长即为EF与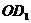 间的距离,由于G是OA中点,O是AC中点,且
间的距离,由于G是OA中点,O是AC中点,且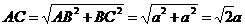 ,∴
,∴  ,即EF与
,即EF与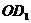 间的距离为
间的距离为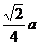 .
.
504. 如图9-18,已知P为△ABC所在平面外一点,PC⊥AB,PC=AB=2,E、F分别为PA和BC的中点.
(1)求证:EF与PC是异面直线;
(2)EF与PC所成的角;
(3)线段EF的长.
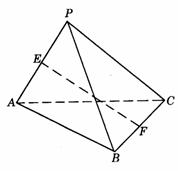
解析:(1)用反证法.假设EF与PC共面于a,则直线PE、CF共面a,则A∈a,B∈a,于是P与A、B、C共面于a,这与已知“P是平面ABC外一点”矛盾.故EF与PC是异面直线.
(2)取PB中点G,连结EG、FG,由E、F分别是线段PA、BC中点,有EG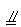
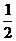 AB,GF
AB,GF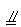
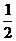 PC
∴ ∠GFE为异面直线EF与PC所成的角,∠EGF是异面直线PC与AB所成的角,∵ PC⊥AB,∴
EG ⊥GF,即∠EGF=90°.∵
PC=AB=2,∴ EG=1,GF=1,故△EFG是等腰直角三角形,∴ ∠GFE=45°,即EF与PC所成的角是45°.
PC
∴ ∠GFE为异面直线EF与PC所成的角,∠EGF是异面直线PC与AB所成的角,∵ PC⊥AB,∴
EG ⊥GF,即∠EGF=90°.∵
PC=AB=2,∴ EG=1,GF=1,故△EFG是等腰直角三角形,∴ ∠GFE=45°,即EF与PC所成的角是45°.
(3)由(2)知Rt△EGF中EG=1,GF=1,∠EGF=90°,∴
EF=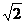
503. 借助两支铅笔,试研究以下问题:
(1)在平面内,过直线外一点有多少条直线与已知直线平行?在空间呢?
图9-17
(2)在一个平面内,过一点有多少条直线与已知直线垂直?在空间呢?
(3)在一个平面内,与该平面内的已知直线所成角为60°的直线有多少条?这些直线与已知直线的位置关系如何?在空间,与一条直线所成角为60°的直线有多少条?这些直线与已知直线的位置关系如何?
解析:(1)在一个平面内,过直线外一点有且只有一条直线与已知直线平行;在空间也如此.
(2)在一个平面内,过一点(该点可在直线上,也可在直线外)有且只有一条直线与已知直线垂线;在空间过直线上或直线外一点都有无数条直线和已知直线垂直,这无数条直线在过已知点的一个平面上(以后可知该平面与直线垂直).
(3)在一个平面内,与已知直线成60°角的直线有无数条,这无数条直线平行,且都与已知直线相交;在空间也是有无数条直线与已知直线成60°角,它们与已知直线位置关系是相交或异面.
502. 在空间四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,得到四边形EFGH.
(1)四边形EFGH是______________;
(2)当对角线AC=BD时,四边形EFGH是______________;
(3)当对角线满足条件______________时,四边形EFGH是矩形;
(4)当对角线AC、BD满足条件_______时,四边形EFGH是正方形.
解析:(1)由三角形中位线定理可知EF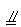
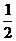 AC,HG
AC,HG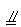
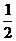 AC,于是EF
AC,于是EF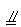 HG,故四边形EFGH为平行四边形;
HG,故四边形EFGH为平行四边形;
(2)当AC=BD时,由EF=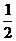 AC,EH=
AC,EH=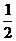 BD,得EF=EH,即平行四边形EFGH的邻边相等,故平行四边形EFGH为菱形;
BD,得EF=EH,即平行四边形EFGH的邻边相等,故平行四边形EFGH为菱形;
(3)要使平行四边形EFGH为矩形,需且只须一个角是直角.如需EF⊥FG,则AC⊥BD;
(4)要使平行四边形EFGH为正方形,需且只须AC⊥ BD,且AC=BD;
501. 在长方体ABCD-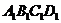 中,AB=2,
中,AB=2,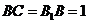 ,M、N分别是AD、DC的中点.
,M、N分别是AD、DC的中点.
(1)证明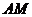 ∥
∥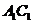 ;
;
(2)求异面直线MN与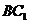 所成角的余弦值.
所成角的余弦值.
解析:(1)∵
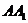 ∥
∥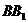 ∥
∥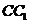 ,
,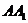 =
=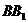 =
=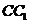 ,∴
,∴ 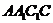 是平行四边形,∴AC∥
是平行四边形,∴AC∥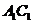 ,又MN∥AC,因此,MN∥
,又MN∥AC,因此,MN∥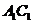 .
.
(2)由(1),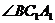 是异面直线MN与
是异面直线MN与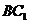 所成角.在△
所成角.在△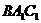 中,
中,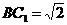 ,
,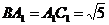 .于是有
.于是有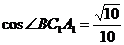 .
.
500. 如图9-16,在棱长为a的正方体ABCD- 中,求异面直线AC和
中,求异面直线AC和 的距离.
的距离.
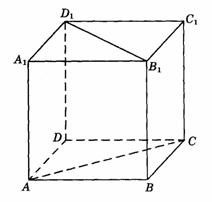
解析:连结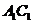 交
交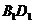 于
于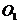 ,连结BD交AC于O,连结
,连结BD交AC于O,连结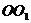 ,在矩形
,在矩形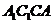 中,
中,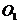 是
是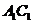 中点,O是AC中点,则
中点,O是AC中点,则 于O.同理
于O.同理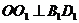 于
于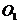 ,∴
,∴ 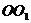 是异面直线AC和
是异面直线AC和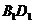 的公垂线.∵
的公垂线.∵  =
= =a,∴ AC与
=a,∴ AC与 间的距离为a.
间的距离为a.
499. 如图9-15,已知A是平面BCD外一点,满足AC=BD,M、N、P、Q分别是BC、CD、DA、AB的中点.求证:QN⊥PM.
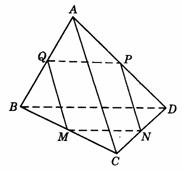
解析:在△ABC中,∵
Q是AB中点,M是BC中点,∴
MQ∥AC,且MQ=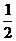 AC,同理PN∥AC,且PN=
AC,同理PN∥AC,且PN=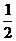 AC.∴
QM
AC.∴
QM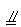 PN.∴
四边形MNPQ是平行四边形,又 ∵ PQ=
PN.∴
四边形MNPQ是平行四边形,又 ∵ PQ=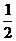 BD,QM=
BD,QM=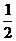 AC,AC=BD,∴
PQ=QM,∴
平行四边形MNPQ是菱形,∴
QN⊥PM.
AC,AC=BD,∴
PQ=QM,∴
平行四边形MNPQ是菱形,∴
QN⊥PM.
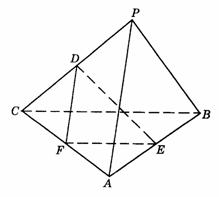
498. 如图9-13,P是平面ABC外一点,PA=4,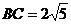 ,D、E分别为PC和AB的中点,且DE=3.求异面直线PA和BC所成角的大小.
,D、E分别为PC和AB的中点,且DE=3.求异面直线PA和BC所成角的大小.
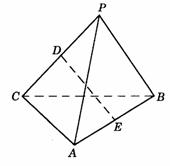
解析:取AC中点F,连结DF、EF,在△PAC中,∵
D是PC中点,F是AC中点,则DF∥PA,同理可得EF∥BC,∴
∠DFE为异面直线PA与BC所成的角.在△DEF中,DE=3,又DF=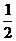 PA=2,EF=
PA=2,EF=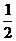 BC=
BC=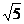 ,∴
,∴ 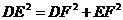 ,∴ ∠DFE=90°,即异面直线PA与BC所成的角为90°.
,∴ ∠DFE=90°,即异面直线PA与BC所成的角为90°.
497. 如图9-12,O是平面ABC外一点,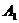 、
、 、
、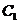 分别在线段OA、OB、OC上,且满足
分别在线段OA、OB、OC上,且满足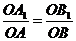 ,
,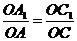 .求证:△ABC∽△
.求证:△ABC∽△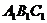 .
.
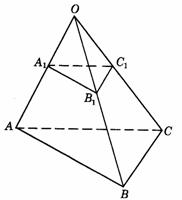
解析:∵ 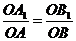 ,
,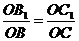 ,∴
,∴ 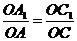 .在△AOB中,由
.在△AOB中,由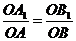 ,∴
,∴ 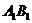 ∥AB,同理
∥AB,同理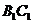 ∥BC,∵
∥BC,∵
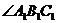 与∠ABC方向相同,∴
与∠ABC方向相同,∴
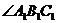 =∠ABC,同理
=∠ABC,同理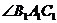 =∠BAC,∴
△
=∠BAC,∴
△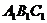 ∽△ABC.
∽△ABC.
496. 如图9-11,在正方体ABCD-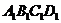 中,E、F分别是棱
中,E、F分别是棱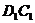 、
、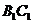 的中点,求证:EF∥BD,且
的中点,求证:EF∥BD,且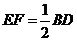 .
.
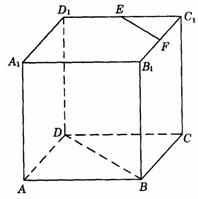
解析:连结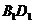 .∵
.∵ 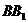 ∥
∥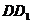 ,∴ 四边形
,∴ 四边形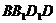 是平面图形,又∵
是平面图形,又∵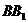 =
=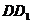 ,∴ 四边形
,∴ 四边形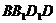 是平行四边形,∴ BD
是平行四边形,∴ BD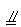
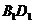 ,在△
,在△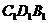 中,∵ E、F分别是
中,∵ E、F分别是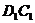 与
与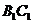 的中点,∴ EF
的中点,∴ EF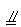
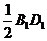 ,由公理4有EF∥BD,且有
,由公理4有EF∥BD,且有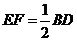 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com