
275. 直线a、b是异面直线,a⊥平面α,b⊥平面β,a⊥b,求证:α⊥β.
证明 过b上任意一点作直线a′,使a∥a′.∵a⊥b,∴a⊥b.
设相交直线a′、b确定一个平面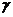 ,
,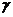 ∩β=c.∵b⊥β,c
∩β=c.∵b⊥β,c β,∴b⊥c.
β,∴b⊥c.
在平面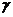 内,b⊥c,b⊥a′,∴a′∥c.∴a∥a′∥c.又∵a⊥α,∴c⊥α,c
内,b⊥c,b⊥a′,∴a′∥c.∴a∥a′∥c.又∵a⊥α,∴c⊥α,c β,∴β⊥α
β,∴β⊥α
272. 设两个平面互相垂直,则( ).
A.一个平面内的任何一条直线都垂直于另一个平面
B.过交线上一点垂直于一个平面的直线必在另一个平面上
C.过交线上一点垂直于交线的直线,必垂直于另一个平面
D.分别在两个平面内的两条直线互相垂直
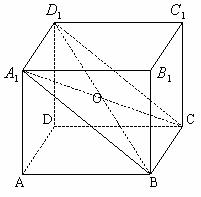
解析:B.如图答9-38,在正方体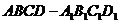 中,平面
中,平面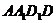 ⊥平面ABCD,其中
⊥平面ABCD,其中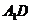
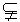 平面
平面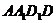 ,但
,但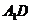 不垂直平面ABCD,故A不正确.点D在交线AD上,
不垂直平面ABCD,故A不正确.点D在交线AD上,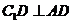 ,但
,但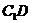 不垂直平面ABCD,故C不正确.
不垂直平面ABCD,故C不正确.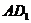
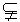 平面
平面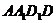 ,AC
,AC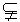 平面ABCD,但
平面ABCD,但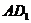 与AC不垂直,故D不正确.
273. 如图9-43,∠AOB是二面角a -CD-b 的平面角,AE是△AOB的OB边上的高,回答下列问题,并说明理由:
与AC不垂直,故D不正确.
273. 如图9-43,∠AOB是二面角a -CD-b 的平面角,AE是△AOB的OB边上的高,回答下列问题,并说明理由:
(1)CD与平面AOB垂直吗?
(2)平面AOB与a 、b 垂直吗?
(3)AE与平面b 垂直吗?
解析:(1)∵ ∠AOB是二面角a -CD-b 的平面角,∴ OB⊥CD,OA⊥CD,∴ CD⊥平面AOB.
(2)∵ CD⊥平面AOB,CD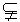 a ,∴ a ⊥平面AOB.同理b ⊥平面AOB.
a ,∴ a ⊥平面AOB.同理b ⊥平面AOB.
(3)∵ CD⊥平面AOB,∵ AE 平面AOB,∴ CO⊥AE,又∵ AE⊥OB,CD∩OB=O,∴ AE⊥平面BCD,即AE⊥b .
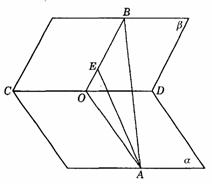
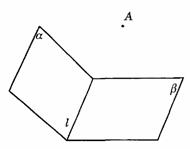
274. 如图9-44,以等腰直角三角形的斜边BC上的高AD为折痕,使△ABD和△ACD折成相垂直的两个面.求证:BD⊥CD,∠BAC=60°.
平面AOB,∴ CO⊥AE,又∵ AE⊥OB,CD∩OB=O,∴ AE⊥平面BCD,即AE⊥b .
274. 如图9-44,以等腰直角三角形的斜边BC上的高AD为折痕,使△ABD和△ACD折成相垂直的两个面.求证:BD⊥CD,∠BAC=60°.

图9-44
解析:∵ AD是等腰△ABC底边BC上的高线,∴ AD⊥BD,AD⊥DC,∴ ∠BDC是二面角B-AD-C的平面角,∵ 平面ABD⊥平面ACD,∴ ∠BDC=90°,即BD⊥DC.连结BC,设AD=a,则BD=DC=AD=a,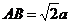 ,
,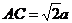 ,
,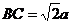 ,∴ △ABC是正三角形,∴ ∠BAC=60°
,∴ △ABC是正三角形,∴ ∠BAC=60°
271. 下列命题中正确的是( ).
A.平面a 和b 分别过两条互相垂直的直线,则a ⊥b
B.若平面a 内的一条直线垂直于平面b 内的两条平行直线,则a ⊥b
C.若平面a 内的一条直线垂直于平面b 内的两条相交直线,则a ⊥b
D.若平面a 内的一条直线垂直于平面b 内的无数条直线,则a ⊥b
解析:C.a
内的直线l垂直b
内的相交直线a、b,则l⊥b
.∵ l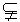 a ,∴ a ⊥b
.
a ,∴ a ⊥b
.
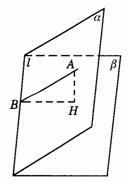

270. 若二面角a -l-b 的一个半平面a 上有一个点A,点A到棱l的距离是它到另一个平面b 的距离的2倍,则这个二面角的大小为( ).
A.90° B.60° C.45° D.30°
解析:D.作AH⊥b 交b 于H,作HB⊥l于B,连结AB,由三垂线定理,HB⊥l,∴ ∠ABH为二面角a -l-b 的平面角,由已知在Rt△ABH中,AB=2AH,∴ ∠ABH=30°.
269. 如图9-42,立体图形A-BCD中,AC=AD,BC=BD.求作二面角A-CD-B的平面角,并说明理由.

解析:取CD中点E,连结AE、BE,∵ AC=AD,∴ AE⊥CD.∵ BC=BD,∴ BE⊥CD,∴ ∠AEB为二面角A-CD-B的平面角.
268. 根据叙述作图,指出二面角a -l-b 的平面角,并证明.
(1)已知a ∩b =l,A∈l(图9-39).在a 内作PA⊥l于A,在b 内作QA⊥l于A.
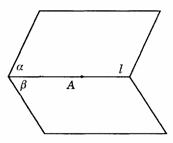
图9-39
(2)已知a
∩b =l,A∈a
,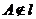 (图9-40).作AP⊥b 于P,在a 内作AQ⊥l于Q,连结PQ.
(图9-40).作AP⊥b 于P,在a 内作AQ⊥l于Q,连结PQ.
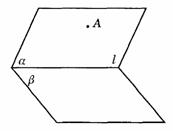
图9-40
(3)已知a
∩b =l,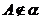 ,
,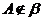 (图9-41).作AP⊥a
于P,AQ⊥b 于Q,l∩平面PAQ=H,连结PH、QH.
(图9-41).作AP⊥a
于P,AQ⊥b 于Q,l∩平面PAQ=H,连结PH、QH.

解析:(1)PA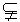 a ,QA
a ,QA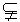 b ,PA⊥l,QA⊥l,∴ ∠PAQ为二面角的平面角.
b ,PA⊥l,QA⊥l,∴ ∠PAQ为二面角的平面角.
(2)∵ AP⊥b ,∴ PQ为AQ在平面b 内的射影,∵ AQ⊥l,根据三垂线定理,有PQ⊥l,∴ ∠AQP为二面角的平面角(如图答9-35).
(3)∵ AP⊥a ,∴ AP⊥l,∵ AQ⊥b ,∴ AQ⊥l,∴ l⊥平面PAQ,∵ PH·QH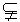 平面PAQ,∴ l⊥PH,l⊥QH,∴ ∠PHQ为二面角的平面角(如图答9-36).
平面PAQ,∴ l⊥PH,l⊥QH,∴ ∠PHQ为二面角的平面角(如图答9-36).
267.长方体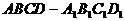 中,
中,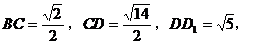 则
则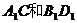 所成角的大小为______________。
所成角的大小为______________。
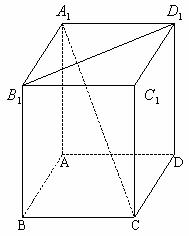
解析:如图所示,将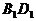 平移到
平移到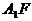 ,则在
,则在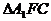 中
中
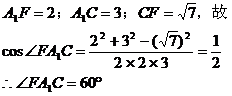
266. 正方体的两条体对角线所夹角的正弦值为______________。
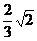
解析:易知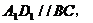 故
故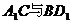 两条体对角线相交,设交点为O(如图),则
两条体对角线相交,设交点为O(如图),则 即为所成的角。
即为所成的角。
设正方体棱长为1,则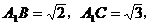
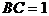 ,所以
,所以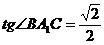 ,而
,而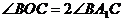 ,故
,故
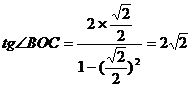 ,即
,即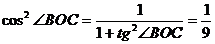 ,
,
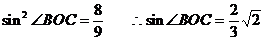
265.试证:两两相交且不全过同一点的四条直线共面.
解析:(1)设a、b、c、d四条直线两两相交,且不过同一点,并且无三线共点.
记 a∩b=A,a∩c=C,c∩b=B,
∵ a∩b=A,∴ a、b确定平面α.
∴ B∈b,C∈a. ∴ B、C∈α.
∴
BC α,即c
α,即c α,同理d
α,同理d α
α
从而 a、b、c、d共面
(2)若有三线共点,不妨设b、c、d相交于A,
a∩b=B,a∩c=C,a∩d=D.
∴ a与A可确定平面α.
∵
B∈a.
∴B∈α,于是b α.
α.
同理,c α,d
α,d α.
α.
从而a、b、c、d共面.
264.异面直线l1、l2,它们之间的距离为1,所成角是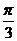 ,它们的公垂线是AB,A∈l1,B∈l2.E∈l1,F∈l2,AE=BF=1,求EF的长.
,它们的公垂线是AB,A∈l1,B∈l2.E∈l1,F∈l2,AE=BF=1,求EF的长.

解析:如图,用异面直线l1、l2作为长方体的上、下底面的对角线,公垂线AB为高.
①EF的长即是正方形PEE′F的对角线长,为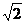 .
.
②侧面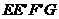 的对角线
的对角线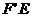 ,用勾股定理得
,用勾股定理得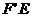 =2,即为所求.
=2,即为所求.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com