595. 直线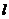与平面α所成角θ的范围是(　 )

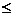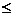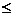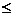　A、0°<θ<90°　　 B、0°θ90°　 C、0°<θ<180°　 D、0°θ180°

解析：B

594. 经过两条平行直线，有且只有一个平面

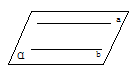证明：因为当两条直线在同一个平面内，且不相交时叫做平行线，所以两条平行直线a和b必在某个平面α内，就是说过两条平行直线有一个平面．如果过a和b还有一个平面β，那么在a上的任意一点A一定在β内这样过点A和直线b有两个平面α和β，这和推论1矛盾，所以过平行直线a和b的平面只有一个．

593. 经过两条相交直线，有且只有一个平面

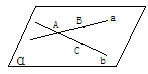　　 证明：如图：设直线a、b相交于点A，在a、b上分别取不同于点A的点B、C，得不在一直线上的三点A、B和C，过这三点有且只有一个平面α(公理3)，因此a、b各有两点在平面α内，所以a、b在平面α内，因此平面α是过相交直线a、b的平面．

如果过直线a和b还有另一个平面β，那么A、B、C三点也一定都在平面β内，这样过不在一条直线上的三点A、B、C就有两个平面α、β了，这和公理3矛盾，所以过直线a、b的平面只有一个．

592. 直线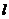上有两点到平面α的距离相等，这条直线和平面α的位置如何？

解析：(1)若直线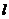上的两点到平面α的距离都等于0，这时直线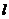在平面α内(如图)

(2)若直线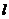上的两点在平面α的两侧,且到平面α的距离相等,这时直线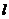与平面α相交(如图)．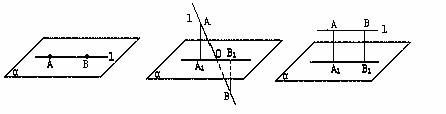

(3)若直线l上的两点在平面α的同一侧，且到平面α的距离相等(如图)．

∵AA₁⊥α于点A₁，BB₁⊥α于点B₁．又 A、B均在l上，且在α的同侧．∴AA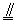₁ BB₁

∴AA₁BB₁为一平行四边形．∴AB∥A₁B₁ ∴这时直线l与平面α平行．

想一想：若直线l上各点到平面α的距离都相等，那么直线l和平面α的位置关系又怎样？

591. 两个惟一性定理．

(1)过一点有且只有一条直线和一已知平面垂直

(2)过一点有且只有一个平面和一已知直线垂直

过点A垂直于直线a的所有直线都在过点A，且垂直于直线a的平面内，试证之．

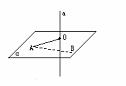已知：A∈α，a⊥α于点O，AB⊥a．求证：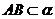

证明：假AB不在平面α内，连结AO．

∵a⊥α∴a⊥AO．又a⊥AB，且AO∩AB=A．

∴a垂直于相交直AO、AB所确定的平面β．

说明：　关于直线和平面垂直的问题中，有两个基本作图：

(1)过一点有且只有一条直线和一个平面垂直．(2)过一点有且只有一个平面和一条直线垂直．

这两个基本作图可作为公理直接使用．

590. 空间四边形ABCD中，P、Q、R分别AB、AD、CD 的中点，平面PQR交BC于S , 求证：四边形PQRS为平行四边形。

　证明：∵PQ为AB、AD中点　 ∴PQ‖BD

　又PQ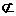平面BCD ，BD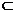平面BCD　 　∴　 PQ‖平面BCD

　又平面PQR∩平面BCD＝RS , PQ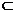平面RQR 　∴　 PQ‖RS

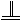
　∵R为DC中点,∴ S为BC中点,∴PQ　　 RS　 ∴ PQRS 为平行四边形

评述:灵活运用线面平行的判定定理和性质定理,“线线平行 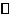线面平行”是证平行关系的常用方法。

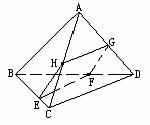
变式题：如图，在四面体ABCD中，截面EFGH是平行四边形．求证：AB∥平面EFG．

证明　∵面EFGH是截面．∴点E，F，G，H分别在BC，BD，DA，AC上．∴EH 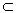面ABC，GF 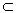面ABD，由已知，EH∥GF．∴EH∥面ABD．又　 ∵EH 面BAC，面ABC∩面ABD=AB∴EH∥AB．

∴AB∥面EFG．

589. 已知直线a∥b，c∩a=A，c∩b=B。求证：a、b、c在同一平面内。

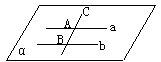证明：∵a∥b

　　　 ∴经过a、b可确定一个平面α

　　　 ∵c∩a=A，∴A∈a，而a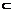α

　　　 ∴A∈α，同理B∈α

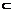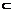　　　 则ABα，即c α

　　　 ∴a、b、c在同一平面α内

点评：利用a∥b，可确定平面α，易证c 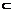α。若利用c∩a=A，也可确定平面α，但证b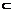α就较困难。因此，选择恰当的点或线确定平面是非常重要的。

588. 在四面体ABCD中，已知点M，N，P分别在棱AD，BD，CD上，点S在平面ABC内，画出线段SD与过点M，N，P的截面的交点O。

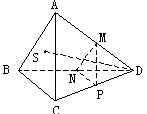解析：图中，SD与平面MNP的交点O点画在△MNP内的任何位置好象都“象”，即直观上不能直接看出画在何处才是准确的。采用上一题的思想方法，找出经过直线SD的平面，如平面ASD(平面CSD…)，作出它与平面MNP的交线。

解：连接AS交BC于E，连ED交NP于F，连MF。

∵M∈AD，AD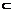平面AED，

∴M∈平面AED

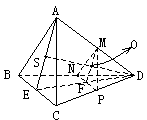
∵F∈ED，ED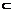平面AED，

∴F∈平面AED

又M∈平面MNP，F∈平面MNP，

∴平面AED∩平面MNP=MF

∵O∈SD，SD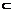平面AED，

∴O∈平面AED，又O∈平面MNP

则O∈MF

即O为MF与SD的交点。

587. 四面体ABCD中，AB=CD，AC=BD，AD=BC，则∠BAC+∠CAD+∠DAB=　　　　　 。

解析：180°

四个三角形均是全等的三角形，故所求三个角即其中任一三角形的三个内角

586. 正方体的12条面对角线所在的直线中，互相异面的直线共有　　　 对。

解析：30

面对角线中，与AC相交的有5条，平行的有1条，(自身为1条)故与AC异面的直线有12-5-1-1=5(条)。

则共有12×5×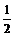=30(对