
171. 如图:已知△ABC在平面α外,AB∩α=P,AC∩α=R,BC∩α=Q。
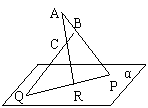 求证:P、Q、R三点共线。
求证:P、Q、R三点共线。
解析:点在线上,线在面内,可得点在面内,证明P,Q,R三个点是平面
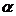 与平面ABC的公共点,即可。
与平面ABC的公共点,即可。
7.提示:只需证明P、Q、R为平面ABC与α的公共点;
170. 如图:已知直线l与平行直线a、b、c都相交,
如图:已知直线l与平行直线a、b、c都相交,
求证:l与a、b、c共面。
设L∩a=A,
l∩b=A,L∩c=C,∵a∥b,∴a、b可确定一个平面α,∵A∈a,B∈b,∴A∈α,B∈α,∴AB α,即L
α,即L α.∵b∥c,∴b、c可确定一个平面β,
α.∵b∥c,∴b、c可确定一个平面β,
同理l β.∵α、β均过相交直线b、l,∴α、β重合,∴a、b、c、l共面;
β.∵α、β均过相交直线b、l,∴α、β重合,∴a、b、c、l共面;
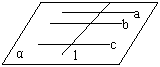
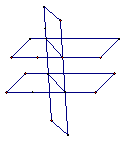
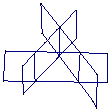
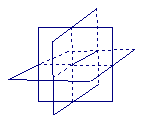
169. 一个平面将空间分成几部分?二个平面将空间分成几部分?三个平面将空间分成几部分?
解析:2部分,3或4部分,4或6或7或8部分
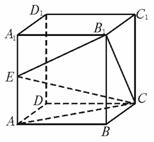
168. 正方体ABCD-A1B1C1D1中,E为棱AA1的中点,求平面EB1C和平面ABCD所成二面角的大小.
解:△EB1C在底面ABCD内的射影三角形为Rt△ABC.
因E点射影为A,B1点射影为B.
设正方体棱长为a,
则S△ABC=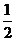 a2.
a2.
又在△EB1C中,
B1E=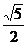 a,B1C=
a,B1C=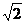 a,EC=
a,EC=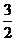 a,
a,
故cos∠B1EC=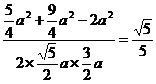 .
.
∴ sin∠B1EC=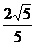 .
.
∴ S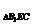 =
=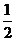 ×
×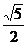 a·
a·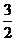 a·
a·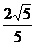 =
=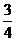 a2.
a2.
设面EB1C和面ABCD所成的二面角为q,
则cosq=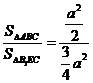 =
=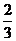 .
.
那么所求二面角的大小为arccos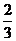 .
.
评述:此题属无棱二面角问题,图中没有二面角的棱,我们也可以去找到棱来解决,但这里通过射影而直接求角更方便.S′=S△ABC,S=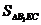 .
.
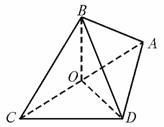
167.四棱锥P-ABCD的底面是边长为a的正方形,PB垂直面ABCD,证明无论四棱锥的高怎样变化,面PAD与面PCD所成的二面角恒大于90°.
解析::注意到题目中所给的二面角,面PAD与面PCD的棱为PD,围绕PD而考虑问题解决途径.
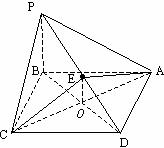
证法一:利用定义法
经A在PDA平面内作AE⊥PD于E,连CE.
因底是正方形,故CD=DA.
△CED≌△AED,AE=EC,∠CED=∠AED=90°,
则CE⊥PD.
故∠CEA是面PAD与面PCD所成二面角的平面角.
设AC与BD交于O,连EO,则EO⊥AC.
因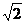 OA=
OA=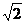 ×
×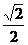 =a,AE<AD<a.
=a,AE<AD<a.
cos∠AEC=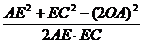 =
=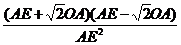 <0.
<0.
所以面PAD与面PCD所成的二面角恒大于90°.
证法二:运用三垂线法
∵ PB⊥面ABCD,则PB⊥AD,又AD⊥AB,
∴ AD⊥面PAB,即面PAB⊥面PAD.
过B作BE⊥PA,则BE⊥面PAD.
在面PBC内作PG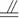 BC,连GD.
BC,连GD.
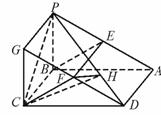
经C作CF⊥面PAD于F,
那么连结EF,有EF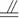 AD.
AD.
经F作FH⊥PD于H,连CH,
则∠FHC是所求二面角平面角的补角.
因CF⊥FH,故∠FHC是锐角.
则面PAD与面PCD所成二面角大于90°.
此结论证明过程中与棱锥高无关.
证法三:利用垂面法找平面角.
在证法一所给图形中
连AC、BD,因AC⊥BD,PB⊥面ABCD,
∴ AC⊥PD.
经A作AE⊥PD于E,那么有PD⊥面AEC,连CE,
即PD⊥CE.
故PD与平面AEC垂直后,面AEC与面ADC及面ADP的交线EA、EC构成角∠CEA就是二面角的平面角.
以下同证法一.
166. 一张菱形硬纸板ABCD的中心是点O,沿它的一条对角线AC对折,使BO⊥DO,这时二面角B-AC-D是多少度?要使二面角B-AC-D为60°,点B和D间的距离应是线段BO的几倍?
解:因ABCD是菱形,故AC⊥BD.
沿对角线AC折为空间图形后BO⊥AC,DO⊥AC.
∠BOD就是二面角B-AC-D的平面角.
因BO⊥OD,故∠BOD=90°,
即二面角B-AC-D是90°.
要使二面角B-AC-D为60°.
因BO=OD,故△BOD是等边三角形,
此时BD=BO.
165. 自二面角内一点分别向这个二面角的两个面引垂线,求证:它们所成的角与这个二面角的平面角互补.
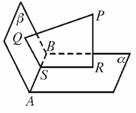
证明:如图PQ⊥b,PQ⊥AB,
PR⊥a,PR⊥AB,
则AB⊥面PQR.
经PQR的平面交a、b于SR、SQ,
那么AB⊥SR,AB⊥SQ.
∠QSR就是二面角的平面角.
因四边形SRPQ中,∠PQS=∠PRS=90°,
因此∠P+∠QSR=180°.
164. 已知二面角a-l-b是45°角,点P在半平面a内,点P到半平面b的距离是h,求点P到棱l的距离.
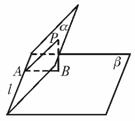
解:经P作PB⊥b于B,
经P在平面a内作PA⊥l于A.
连AB,则AB⊥l.
∠PAB就是二面角的平面角,∠PAB=45°.
那么在Rt△PAB中,PB=h,PA=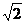 h.
h.
163.如图,立体图形V-ABCD中,底面是正方形ABCD,其他四个侧面都是全等的正三角形,画出二面角V-AB-C的平面角,并求它的度数.
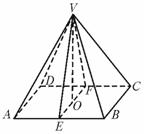
解:设底面边长为a,则侧面三角形的边长也为a.
取AB的中点E,DC中点F,连VE、EF.
∵ 侧面△VAB是正三角形,
∴ VE⊥AB.
又EF∥BC,BC⊥AB,∴ EF⊥AB.
∠VEF就是V-AB-C的平面角.
cos∠VEF=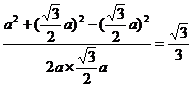 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com