426. 地球半径为R，A、B两地都在北纬45°线上，且A、B的球面距离为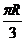，求A、B两地经度的差.

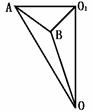
解析：如图，O为球心，O₁为北纬45°小圆的圆心，知A、B的球面距离，就可求得∠AOB的弧度数，进而求得线段AB的长，在ΔAO₁B中，∠AO₁B的大小就是A、B两地的经度差.

解：　 设O₁是北纬45°圆的中心，

∵A、B都在此圆上，

∴O₁A＝O₁B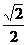＝R.

∵A、B的球面距离为，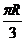

∴∠AOB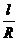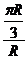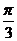＝＝＝,ΔAOB为等边三角形.

AB＝R，在ΔAO₁B中，

∵O₁A²+O₁B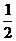²＝R²+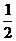R²＝R²＝AB²，

∴∠AO₁B＝90°.

∴A、B两地的经度差是90°.

评析：注意搞清纬度和经度的问题，球面距离三步骤的运用是非常重要的问题.

425. 求证：球的外切正四面体的高是球的直径的2倍.

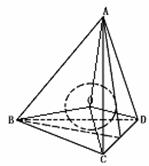
证明： 　设球的半径为R，正四面体的高为h，侧面积为S，则有V_A-BCD＝V_O-ABC+V_O-ABD+V_O-BCD，如图，即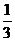Sh＝4×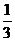SR,∴h＝4R.

424.　 正三棱锥的底面边长是2cm，侧棱与底面成60°角，求它的外接球的表面积.

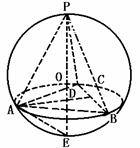
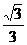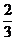
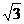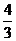
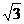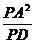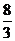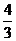解析：如图，PD是三棱锥的高，则D是ΔABC的中心，延长PD交球于E，则PE就是外接球的直径，AD＝AB＝，∠PAD＝60°，∴PD＝AD·tan60°＝2,PA＝，而AP⊥AE，∴PA²＝PD·PE＝＝，R＝，∴S_球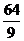＝π(cm)².

423.　 两面都是凸形的镜中，它的面都是球冠形，球半径分别为10cm和17cm，两球心间的距离为21cm，求此镜面的表面积和体积.

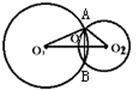
解析：轴截面如图，设O₂C＝x，则CO₁＝21-x,∵AB⊥O₁O₂　 ∴AO₂²-O₂C²＝AO₁²-CO₁²，即10²-x²＝17²-(21-x)²，解得x＝6,CO₁＝15,又设左边球缺的高为h₁,右边的球缺高为h₂，则h₁＝17-15＝2,h₂＝10-6＝4,∴S_表＝2π(17·2+10·4)＝148π(cm)²,V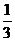＝π［2²(3·10-2)+4²(3·17-4)］＝288π(cm³).

422. 一个圆在平面上的射影图形是(　　 )

A.圆　　　　　　　　　　　　 B.椭圆

C.线段　　　　　　　　　　　 D.圆或椭圆或线段

解析：D

421.　 地球半径为R，在北纬45°圈上有A、B两点，它们的经度差为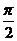，求球面上A、B两点间球面距离.

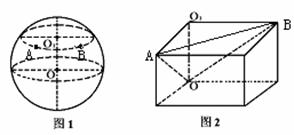
解析：本题关键是求出∠AOB的大小，(如图1)现在我们将这个球的截面问题转化为较为熟悉的长方体问题.如图2，以O₁O，O₁A，O₁B为三条相互垂直的棱，可构造一个长方体，问题转化为长方体截面ABO内求∠BOA的问题.

解：　 如图2，∵∠O₁OA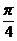＝＝∠O₁OB，OA＝OB＝R，∴OO₁＝O₁A＝O₁B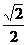＝R　 ∴AB²＝O₁A²+O₁B²＝R，　 ∴ΔAOB为等边Δ，　 ∴∠AOB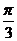＝，A、B间的球面距离为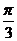R.

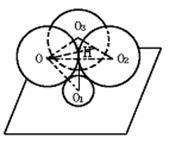
420.　 在桌面上有三个球两两相切，且半径都为1，在桌面与三球间放置一个小球，使它与三个球相切.求此小球半径.

解析： 如图，球O为放置在桌面上与已知三球相切的半径为r的小球，过O作O₁O₂O₃平面的垂线，垂足为H，它一定是ΔO₁O₂O₃的中心，连接O₁H，O₁O，在RtΔO₁OH中，O₁H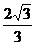＝，OH＝1-r,OO₁＝1+r,∴OO₁²＝O₁H²+OH²，即(1+r)²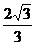＝()²+(1-r)²，解得r＝.

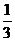419. 已知球的两个平行截面的面积分别为5π和8π，它们位于球心的同一侧且相距是1，那么这个球的半径是(　　 )

A.4　　　　　　 B.3　　　　　　 C.2　　　　　　 D.5

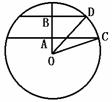
解析： 如图，设球的半径是r，则πBD²＝5π，πAC²＝8π，

∴BD²＝5，AC²＝8.又AB＝1，设OA＝x.

∴x²+8＝r²,(x+1)²+5＝r².

解之，得r＝3

故选B.

418.　 已知四点，无三点共线，则可以确定(　　 )

A.1个平面　　　　　　　 B.4个平面

C.1个或4个平面　　　　 D.无法确定

解析： 因为无三点共线，所以任意三个点都可以确定平面α，若第四个点也在α内，四个点确定一个平面，当第四个点在α外，由公理3知可确定4个平面.故选C.

417.　 下列命题正确的是(　　 )

A.经过两条直线有且只有一个平面

B.经过一条直线和一个点有且只有一个平面

C.如果平面α与β有三个公共点，则两个平面一定是重合平面

D.两个平面α、β有一个公共点，那么它们有且只有一条通过这个点的公共直线

解析：根据公理2、公理3知选D.