
5.(09•福建文综17)抗日战争全面爆发后,八路军主力从集结地开赴华北战场协同友军作战,途中需要( )
A.东渡黄河 B.北渡长江 C.跨越陇海线 D.挺进大别山
答案 A
4.(09•安徽文综16)抗日战争期间,延安“吸引了一个美国军事观察团、一些美国国务院外交官和一个美国总统特使前来访问,另外还有大批外国记者前来采访”。其主要原因是 ( )
A.中共领袖人物的个人魅力
B.中共的抗日主张得到了普遍认同
C.中共坚持抗战赢得了国际友人的广泛同情
D.中共领导的抗日力量在抗战中的地位日显重要
答案 D
3.(09•山东文综12)一位同学查阅《申报》时看到一下报道:“□路方面消息,沪平通车昨日起北上车暂以济南为终点,南下车亦由济南开出,惟津浦客车则仍开至沧州,其以北之情形 不明 。南下各次车抵沪时,均甚拥挤 ”(注:□表示字迹不清)该报道的历史背景是 ( )
A.红军转战陕北,国共军事对峙 B.日本全面侵华,平津局势紧张
C.内战全面爆发,华北战事频繁 D.三大战役结束,长江以北解放
答案 C
2.(09•北京文综19)图8中数字符号标明的地点,都是抗日战争时期注明战役的发生地,其中能为八路军战史提供实地资料的是 ( )
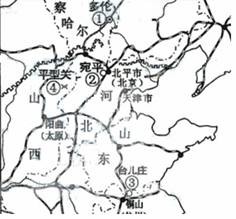
图8
A.① B.② C.③ D.④
答案 C
2009年高考题
1.(09•全国Ⅰ卷文综19)抗日战争期间某战役后,《新华日报》刊载一位中国将领的谈话:“我军……对于一城一寨之得失,初不以为重,主在引敌深入,使其兵力分散,而予敌主力以打击。”以下战役符合上述特征的是 ( )
A.淞沪会战 B.百团大战 C.台儿庄战役 D.平型关战役
答案 C
600. 要修建一座底面是正方形且四壁与底面垂直的水池,在四壁与底面面积之和一定的前提下,为使水池容积最大,求水池底面边长与高的比值.
解析:为了建立体积V的函数,我们选底面边长和高为自变量.
设水池底面边长为a,水池的高为h,水池容积为v,依题意,有a2+4ah=k(k为定值).
∴v=a2h=a2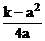 =
=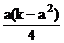 (v>0),
(v>0),
∴v2=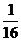 a2(k-a2)2=
a2(k-a2)2=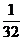 ·2a2(k-a2)(k-a2)
·2a2(k-a2)(k-a2)
≤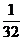 (
(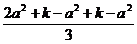 )3=
)3=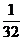 ·
·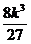 =
=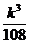 (当且仅当2a2=k-a2时,即k=3a2时等号成立),
(当且仅当2a2=k-a2时,即k=3a2时等号成立),
故 a2+4ah=3a2,
即a∶h=2∶1时,水池容积最大为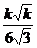 .
.
599. 某人买了一罐容积为V升、高为a米的直三棱柱型罐装进口液体车油,由于不小心摔落地上,结果有两处破损并发生渗漏,它们的位置分别在两条棱上且距底面高度分别为b、c的地方(单位:米).为了减少罐内液油的损失,该人采用罐口朝上,倾斜罐口的方式拿回家.试问罐内液油最理想的估计能剩多少?
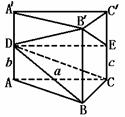
解析:如图所示,建立模型,设直三棱柱为ABC-A′B′C′,破损处为D、E.并且AD=b,EC=c,BB′=a.则罐内所剩液油的最大值即为几何体ABC-DB′E的体积.
连结BD、CD
∵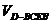 =
=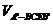 ,
,
而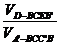 =
=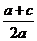 ,
,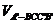 =
=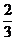 V,
V,
∴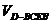 =
=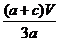 .
.
又∵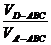 =
=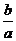 ,∴VD-ABC=
,∴VD-ABC=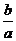 ·
·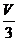 =
=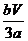 .
.
故 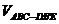 =
=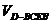 +VD-ABC=
+VD-ABC=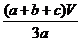 ,即最理想的估计是剩下
,即最理想的估计是剩下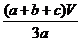 升.
升.
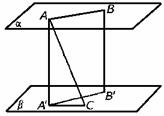
598. 平面α∥平面β,A、B∈α,C∈β,AA′⊥β于A′,BB′⊥β于B′,若AC⊥AB,AC与β成60°的角,AC=8cm,B′C=6cm,求异面直线AC与BB′间的距离.
解析:∵BB′⊥α∴BB′⊥AB 又∵AC⊥AB ∴AB为AC与BB′的公垂线
又∵AB=A′B′ AB∥A′B′ AC⊥A′B′
∴A′C′⊥A′B′
A′B′=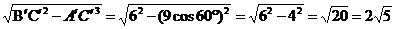
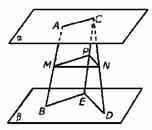
597. AB、CD为夹在两个平行平面α、β间的异面线段,M、N分别为AB、CD的中点,求证:MN∥α.
解析:过C作CE∥AB交β于E,取CE中点P则
AB∥CE AC∥BE MP∥AC BP∥α
(1)MP∥β;(2)PN∥ED?PN∥β.∴面MN∥面β∴MN∥面α,MN∥α
596.两条一异面直线所成的角的范围是?
直线与平面所成的角的范围是?
两个半平面所成二面角的范围是?
斜线与平面所成的角的范围是?
解析: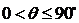 ,
,
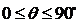 ,直线在平面内或直线与平面平行定为0
,直线在平面内或直线与平面平行定为0
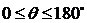 ,规定两个半平面重合时为0,两个半平面展成一个平面为180度。
,规定两个半平面重合时为0,两个半平面展成一个平面为180度。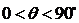
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com