
11.(搬中) 已知椭圆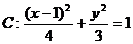 ,F为它的右焦点,直线
,F为它的右焦点,直线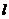 过原点交椭圆C于A、B两点。求
过原点交椭圆C于A、B两点。求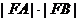 是否存在最大值或最小值?若不存在,说明理由。
是否存在最大值或最小值?若不存在,说明理由。
错解 设A、B两点坐标分别为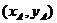 、
、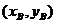
因为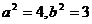
所以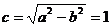
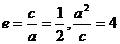
又椭圆中心为(1,0),右准线方程为x=5
所以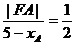
即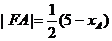
同理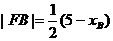
所以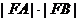
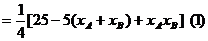
设直线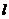 的方程为y=kx,代入椭圆方程得
的方程为y=kx,代入椭圆方程得
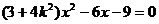
所以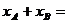
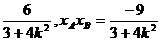
代入(1)式得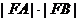
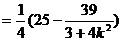
所以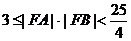
所以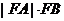 |有最小值3,无最大值。
|有最小值3,无最大值。
剖析 上述错解过程忽视了过原点斜率不存在的直线,当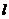 的斜率不存在时,有
的斜率不存在时,有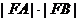
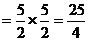
所以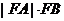 有最小值为
3,最大值为25/4
有最小值为
3,最大值为25/4
10.(搬中)已知双曲线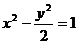 ,问过点A(1,1)能否作直线
,问过点A(1,1)能否作直线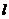 ,使
,使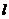 与双曲线交于P、Q两点,并且A为线段PQ的中点?若存在,求出直线
与双曲线交于P、Q两点,并且A为线段PQ的中点?若存在,求出直线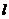 的方程,若不存在,说明理由。
的方程,若不存在,说明理由。
错解 设符合题意的直线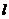 存在,并设
存在,并设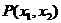 、
、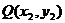
则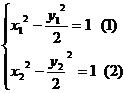
(1)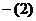 得
得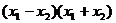
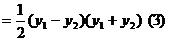
因为A(1,1)为线段PQ的中点,
所以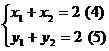
将(4)、(5)代入(3)得
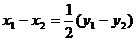
若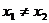 ,则直线
,则直线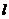 的斜率
的斜率
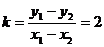
所以符合题设条件的直线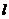 存在。
存在。
其方程为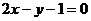
剖析 在(3)式成立的前提下,由(4)、(5)两式可推出(6)式,但由(6)式不能推出(4)(5)两式,故应对所求直线进行检验,上述错解没有做到这一点,故是错误的。
应在上述解题的基础上,再由
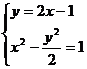
得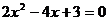
根据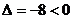 ,说明所求直线不存在。
,说明所求直线不存在。
9. (搬中)椭圆中心是坐标原点,长轴在x轴上,离心率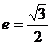 ,已知点P(
,已知点P(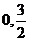 )到椭圆上的点最远距离是
)到椭圆上的点最远距离是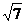 ,求这个椭圆的方程。
,求这个椭圆的方程。
错解 设所求椭圆方程为
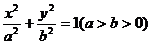
因为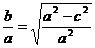
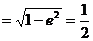
所以a=2b
于是椭圆方程为
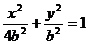
设椭圆上点M(x,y)到点P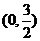 的距离为d,
的距离为d,
则: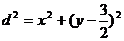
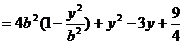
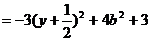
所以当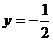 时,
时,
有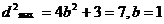
所以所求椭圆方程为
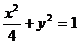
剖析 由椭圆方程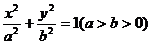
得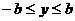
由(1)式知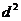 是y的二次函数,
是y的二次函数,
其对称轴为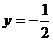
上述错解在于没有就对称轴在区间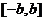 内或外进行分类,
内或外进行分类,
其正确应对f(y)=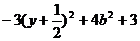 的最值情况进行讨论:
的最值情况进行讨论:
(1)当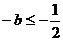 ,即
,即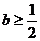 时
时
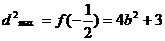 =7
=7
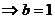 ,方程为
,方程为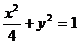
(2)当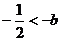 ,
,
即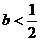 时,
时,
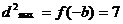
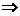
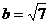
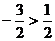 ,与
,与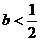 矛盾。
矛盾。
综上所述,所求椭圆方程为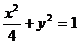
8. (搬中)已知双曲线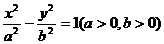 的离心率e=
的离心率e=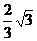 ,
过点A(
,
过点A(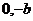 )和B(a,0)的直线与原点的距离为
)和B(a,0)的直线与原点的距离为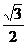 ,直线y=kx+m
,直线y=kx+m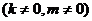 与该双曲线交于不同两点C、D,且C、D两点都在以A为圆心的同一圆上,求m 的取值范围。
与该双曲线交于不同两点C、D,且C、D两点都在以A为圆心的同一圆上,求m 的取值范围。
错解 由已知,有
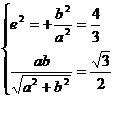
解之得: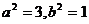
所以双曲线方程为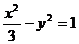
把直线 y=kx+m代入双曲线方程,并整理得:
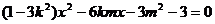
所以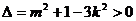 (1)
(1)
设CD中点为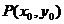 ,
,
则AP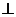 CD,且易知:
CD,且易知:
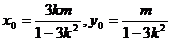
所以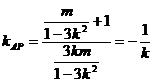
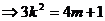 (2)
(2)
将(2)式代入(1)式得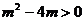
解得m>4或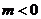
故所求m的范围是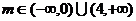
剖析 上述错解,在于在减元过程中,忽视了元素之间的制约关系,将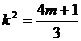 代入(1)
式时,m受k的制约。
代入(1)
式时,m受k的制约。
因为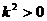
所以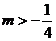
故所求m的范围应为
m>4或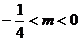
7.(搬中)点P与定点F(2,0)的距离和它到直线x=8的距离比是1:3,求动点P与定点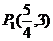 距离的最值。
距离的最值。
错解:设动点P(x,y)到直线x=8的距离为d,则
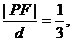
即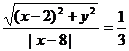
两边平方、整理得
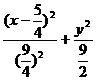 =1 (1)
=1 (1)
由此式可得:
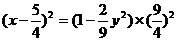
因为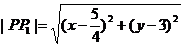
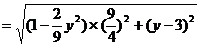
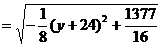
所以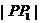
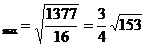
剖析 由上述解题过程知,动点P(x,y)在一椭圆上,由椭圆性质知,椭圆上点的横纵坐标都是有限制的,上述错解在于忽视了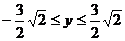 这一取值范围,由以上解题过程知,
这一取值范围,由以上解题过程知,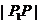 的最值可由二次函数在区间上的单调性给予解决
的最值可由二次函数在区间上的单调性给予解决
即:当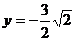 时,
时,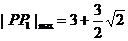
6.(搬中) 已知圆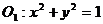 ,圆
,圆
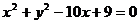 都内切于动圆,试求动圆圆心的轨迹方程。
都内切于动圆,试求动圆圆心的轨迹方程。
错解:圆O2: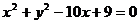
即为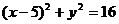
所以圆O2的圆心为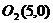 ,半径
,半径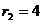 ,
,
而圆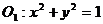 的圆心为
的圆心为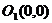 ,半径
,半径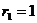 ,
,
设所求动圆圆心M的坐标为(x,y),半径为r
则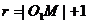 且
且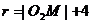
所以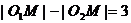
即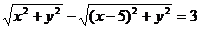
化简得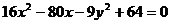
即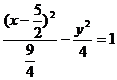 为所求动圆圆心的轨迹方程。
为所求动圆圆心的轨迹方程。
剖析:上述解法将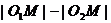 =3看成
=3看成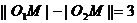 ,误认为动圆圆心的轨迹为双曲线,这是双曲线的概念不清所致。
,误认为动圆圆心的轨迹为双曲线,这是双曲线的概念不清所致。
事实上,|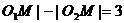 表示动点M到定点
表示动点M到定点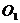 及
及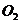 的距离差为一常数3。
的距离差为一常数3。
且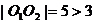 ,点M的轨迹为双曲线右支,方程为
,点M的轨迹为双曲线右支,方程为
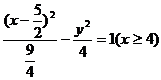
5. (石庄中学)在函数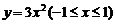 的图象上有A、B两动点,满足AB∥x轴,点M(1,m)(m为常数,m>3)是三角形ABC的边BC的中点,设A点横坐标t,△ABC的面积为f (t).
的图象上有A、B两动点,满足AB∥x轴,点M(1,m)(m为常数,m>3)是三角形ABC的边BC的中点,设A点横坐标t,△ABC的面积为f (t).
(1) 求f (t)的解析表达式;
(2) 若f (t)在定义域内为增函数,试求m的取值范围;
(3) 是否存在m使函数f (t)的最大值18?若存在,试求出m的值;若不存在,请说明理由。
解:(1) f (t) = 2t (m-3t2) 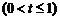
(2) 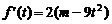
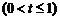 ∵
∵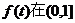 上是增函数.
上是增函数.
∴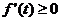
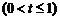 即
即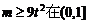 上恒成立.
上恒成立.
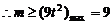 即m的取值范围
即m的取值范围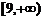
(3) 令f’(t)=0,得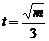 (其中
(其中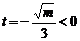 舍去)
舍去)
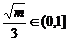 即
即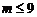 时,在
时,在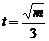 处
处 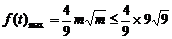 =12,
=12,
此时m的值不存在.
令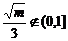 ,即m>9由(2)知f (t)在
,即m>9由(2)知f (t)在 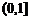 为增函数,
为增函数,
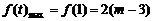 ,由2(m-3)=18得m=12
,由2(m-3)=18得m=12
综上只存在m=12适合题意。
4.(石庄中学)设有半径为3km的圆形村落,A、B两人同时从村落中心出发,B向北直行,A先向东直行,出村后不久,改变前进方向,沿着与村落周界相切的直线前进,后来恰与B相遇,设A、B两人速度一定,其速度比为3:1,问两人在何处相遇?
解:设直线CD的方程为
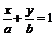
∵圆心O到直线CD的距离3
∴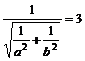 ①
①
∵VA:VB=3:1
在相同时间内有
SA:SB=3:1
∴3b=a+b+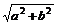 ②
②
由①②解得
a=5
b=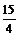
∴CD直线方程为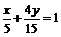
∴A与B在距村心北方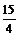 km处相遇
km处相遇
3.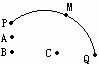 (石庄中学) 如图,A村在B地正北
(石庄中学) 如图,A村在B地正北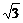 cm处,C村在B地正东4km处,已知弧形公路PQ上任一点到B,C距离之和为8km,现要在公路旁建造一个交电房M分别向A村、C村送电,但C村有一村办工厂用电需用专用线路,不得与民用混线用电,因此向C村要架两条线路分别给村民和工厂送电,要使得所用电线最短,变电房M应建在A村的什么方位,并求出M到A村的距离.
cm处,C村在B地正东4km处,已知弧形公路PQ上任一点到B,C距离之和为8km,现要在公路旁建造一个交电房M分别向A村、C村送电,但C村有一村办工厂用电需用专用线路,不得与民用混线用电,因此向C村要架两条线路分别给村民和工厂送电,要使得所用电线最短,变电房M应建在A村的什么方位,并求出M到A村的距离.
解: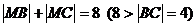 ,∴M在以B,C为焦点,长
,∴M在以B,C为焦点,长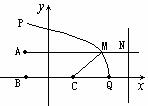 轴长为8的椭圆上,建立如图所示的坐标系,则B(-2,0),C(2,0),
轴长为8的椭圆上,建立如图所示的坐标系,则B(-2,0),C(2,0),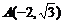 ,
,
求得椭圆方程为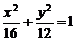 ,其离心率
,其离心率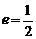 ,右准线为
,右准线为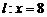 .
.
作MN⊥l于N,则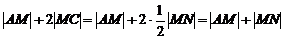 ,由平面几何知识知,当直线MN通过A时,
,由平面几何知识知,当直线MN通过A时,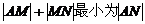 ,此时M的纵坐标为
,此时M的纵坐标为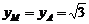 ,
,
∴M的横坐标为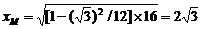 .
.
故得M在A正东且距A为(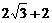 )km处.
)km处.
2. (如中)已知双曲线两焦点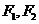 ,其中
,其中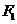 为
为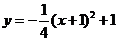 的焦点,两点A (-3,2) B (1,2)都在双曲线上,(1)求点
的焦点,两点A (-3,2) B (1,2)都在双曲线上,(1)求点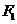 的坐标;(2)求点
的坐标;(2)求点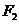 的轨迹方程,并画出轨迹的草图;(3)若直线
的轨迹方程,并画出轨迹的草图;(3)若直线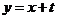 与
与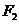 的轨迹方程有且只有一个公共点,求实数 t的取值范围。
的轨迹方程有且只有一个公共点,求实数 t的取值范围。
解答:(1)由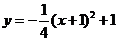 得:
得: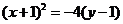
故 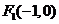
(2)设点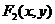
则又双曲线的定义得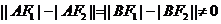
又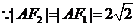
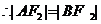 或
或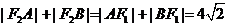
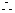 点
点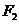 的轨迹是以
的轨迹是以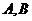 为焦点的椭圆
为焦点的椭圆
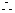
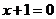 除去点
除去点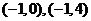 或
或 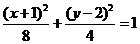 除去点
除去点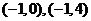 图略。
图略。
(3)联列: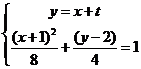 消去
消去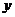 得
得
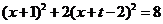 整理得:
整理得: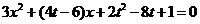
当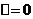 时 得
时 得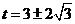 从图可知:
从图可知: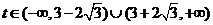 ,
,
又因为轨迹除去点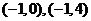 所以当直线过点
所以当直线过点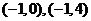 时也只有一个交点,即
时也只有一个交点,即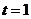 或5
或5
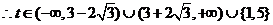
易错原因:(1)非标准方程求焦点坐标时计算易错;(2)求点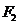 的轨迹时易少一种情况;(3)对有且仅有一个交点误认为方程只有一解。
的轨迹时易少一种情况;(3)对有且仅有一个交点误认为方程只有一解。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com