
(一)选择题
1、已知a,b,a+b成等差数列,a,b,ab成等比数列,且0<logmab<1,则m取值范围是
A、m>1 B、1<m<8 C、m>8 D、0<m<1或m>8
2、设a>0,b>0,a,x1,x2,b成等差数列,a,y1,y2,b成等比数列,则x1+x2与y1+y2的大小关系是
A、x1+x2≤y1+y2 B、x1+x2≥y1+y2
C、x1+x2<y1+y2 D、x1+x2>y1+y2
2、已知Sn是{an}的前n项和,Sn=Pn(P∈R,n∈N+),那么数列{an}
A、 是等比数列 B、当P≠0时是等比数列
C、 当P≠0,P≠1时是等比数列 D、不是等比数列
3、{an}是等比数列,且an>0,a2a4+2a3a5+a4a6=25,则a3+a5等于
A、5 B、10 C、15 D、20
4、已知a,b,c成等差数列,则二次函数y=ax2+2bx+c的图象与x轴交点个数是
A、 0 B、1 C、2 D、1或2
5、设m∈N+,log2m的整数部分用F(m)表示,则F(1)+F(2)+…+F(1024)的值是
A、 8204 B、8192 C、9218 D、8021
7、若x的方程x2-x+a=0和x2-x+b=0(a≠b)的四个根可组成首项为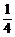 的等差数列,则a+b的值为
的等差数列,则a+b的值为
A、 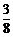 B、
B、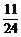 C、
C、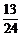 D、
D、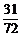
8、 在100以内所有能被3整除但不能被7整除的正整数和是
A、1557 B、1473 C、1470 D、1368
9、从材料工地运送电线杆到500m以外的公路,沿公路一侧每隔50m埋栽一根电线杆,已知每次最多只能运3根,要完成运载20根电线杆的任务,最佳方案是使运输车运行
A、 11700m B、14700m C、14500m D、14000m
10、已知等差数列{an}中,|a3|=|a9|,公差d<0,则使前n项和Sn取最大值的正整数n是
A、4或5 B、5或6 C、6或7 D、8或9
例1、已知数列{an}为等差数列,公差d≠0,其中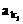 ,
,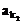 ,…,
,…,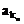 恰为等比数列,若k1=1,k2=5,k3=17,求k1+k2+…+kn。
恰为等比数列,若k1=1,k2=5,k3=17,求k1+k2+…+kn。
解题思路分析:
从寻找新、旧数列的关系着手
设{an}首项为a1,公差为d
∵ a1,a5,a17成等比数列
∴ a52=a1a17
∴(a1+4d)2=a1(a1+16d)
∴ a1=2d
设等比数列公比为q,则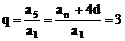
对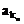 项来说,
项来说,
在等差数列中: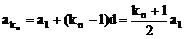
在等比数列中: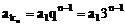
∴ 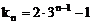
∴ 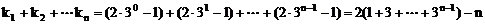
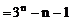
注:本题把k1+k2+…+kn看成是数列{kn}的求和问题,着重分析{kn}的通项公式。这是解决数列问题的一般方法,称为“通项分析法”。
例2、设数列{an}为等差数列,Sn为数列{an}的前n项和,已知S7=7,S15=75,Tn为数列{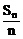 }的前n项和,求Tn。
}的前n项和,求Tn。
解题思路分析:
法一:利用基本元素分析法
设{an}首项为a1,公差为d,则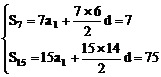
∴ 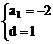
∴ 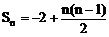
∴ 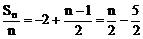
此式为n的一次函数
∴ {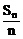 }为等差数列
}为等差数列
∴ 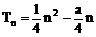
法二:{an}为等差数列,设Sn=An2+Bn
∴ 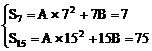
解之得: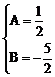
∴ 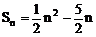 ,下略
,下略
注:法二利用了等差数列前n项和的性质
例3、正数数列{an}的前n项和为Sn,且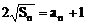 ,求:
,求:
(1)数列{an}的通项公式;
(2)设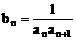 ,数列{bn}的前n项的和为Bn,求证:Bn
,数列{bn}的前n项的和为Bn,求证:Bn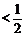 .
.
解题思路分析:
(I)涉及到an及Sn的递推关系,一般都用an=Sn-Sn-1(n≥2)消元化归。
∵ 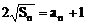
∴ 4Sn=(an+1)2
∴ 4Sn-1=(an-1+1)2(n≥2)
∴ 4(Sn-Sn-1)=(an+1)2-(an-1+1)2
∴ 4an=an2-an-12+2an-2an-1
整理得:(an-1+an)(an-an-1-2)=0
∵ an>0
∴ an-an-1=2
∴ {an}为公差为2的等差数列
在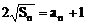 中,令n=1,a1=1
中,令n=1,a1=1
∴ an=2n-1
(II)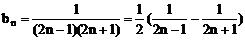
∴ 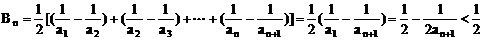
注:递推是学好数列的重要思想,例本题由4Sn=(an+1)2推出4Sn-1=(an-1+1)2,它其实就是函数中的变量代换法。在数列中一般用n-1,n+1等去代替n,实际上也就是说已知条件中的递推关系是关于n的恒等式,代换就是对n赋值。
例4、等差数列{an}中,前m项的和为77(m为奇数),其中偶数项的和为33,且a1-am=18,求这个数列的通项公式。
分析:
利用前奇数项和和与中项的关系
令m=2n-1,n∈N+
则 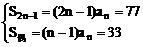
∴ 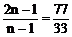
∴ n=4
∴ m=7
∴ an=11
∴ a1+am=2an=22
又a1-am=18
∴ a1=20,am=2
∴ d=-3
∴ an=-3n+23
例5、设{an}是等差数列,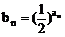 ,已知b1+b2+b3=
,已知b1+b2+b3=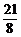 ,b1b2b3=
,b1b2b3=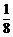 ,求等差数列的通项an。
,求等差数列的通项an。
解题思路分析:
∵ {an}为等差数列
∴ {bn}为等比数列
从求解{bn}着手
∵ b1b3=b22
∴ b23=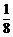
∴ b2=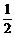
∴ 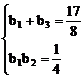
∴ 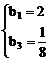 或
或 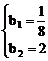
∴ 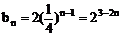 或
或 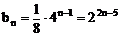
∵ 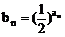
∴ 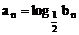
∴ an=2n-3 或 an=-2n+5
注:本题化归为{bn}求解,比较简单。若用{an}求解,则运算量较大。
例6、已知{an}是首项为2,公比为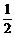 的等比数列,Sn为它的前n项和,
的等比数列,Sn为它的前n项和,
(1)用Sn表示Sn+1;
(2)是否存在自然数c和k,使得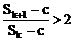 成立。
成立。
解题思路分析:
(1)∵ 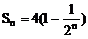
∴ 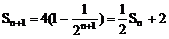
(2)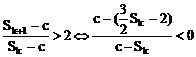 (*)
(*)
∵ 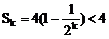
∴ 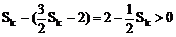
∴ 式(*)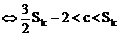 ①
①
∵ Sk+1>Sk
∴ 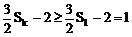
又Sk<4
∴ 由①得:c=2或c=3
当c=2时
∵ S1=2
∴ k=1时,c<Sk不成立,从而式①不成立
∵ 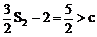
∴ 由Sk<Sk+1得: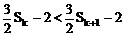
∴ 当k≥2时,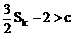 ,从而式①不成立
,从而式①不成立
当c=3时,S12,S2=3
∴ 当k=1,2时,C<Sk不成立
∴ 式①不成立
∵ 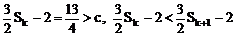
∴ 当k≥3时,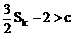 ,从而式①不成立
,从而式①不成立
综上所述,不存在自然数c,k,使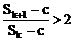 成立
成立
例7、某公司全年的利润为b元,其中一部分作为资金发给n位职工,资金分配方案如下:首先将职工按工作业绩(工作业绩均不相等)从大到小,由1到n排序,第1位职工得资金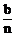 元,然后再将余额除以n发给第2位职工,按此方法将资金逐一发给每位职工,并将最后剩余部分作为公司发展基金。
元,然后再将余额除以n发给第2位职工,按此方法将资金逐一发给每位职工,并将最后剩余部分作为公司发展基金。
(1)设ak(1≤k≤n)为第k位职工所得资金额,试求a2,a3,并用k,n和b表示ak(不必证明);
(2)证明:ak<ak+1(k=1,2,…,n-1),并解释此不等式关于分配原则的实际意义。
解题思路分析:
谈懂题意,理清关系,建立模型
第1位职工的奖金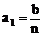
第2位职工的奖金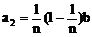
第3位职工的奖金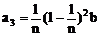
……
第k位职工的奖金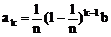
(2)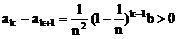
此奖金分配方案体现了“按劳分配”或“不吃大锅饭”等原则。
例8、试问数列{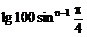 }的前多少项的和最大,并求这个最大值(lg2=0.3010)
}的前多少项的和最大,并求这个最大值(lg2=0.3010)
解题思路分析:
法一: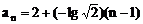
∴ {an}为首项为2,公差为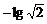 的等差数列
的等差数列
∴ 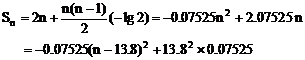
∵ n∈N+
∴ n=14时,(Sn)max=14.35
法二:∵ a1=2>0,d=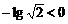
∴ {an}是递减数列,且Sn必为最大值
设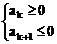
∴ 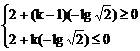
∴ 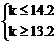
∴ k=14
∴ (Sn)max=S14=14.35
同步练习
4、等差、等比数列的应用
(1)基本量的思想:常设首项、公差及首项,公比为基本量,借助于消元思想及解方程组思想等;
(2)灵活运用等差数列、等比数列的定义及性质,简化计算;
(3)若{an}为等差数列,则{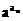 }为等比数列(a>0且a≠1);
}为等比数列(a>0且a≠1);
若{an}为正数等比数列,则{logaan}为等差数列(a>0且a≠1)。
3、等比数列
(1)定义: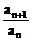 =q(q为常数,an≠0);an2=an-1an+1(n≥2,n∈N+);
=q(q为常数,an≠0);an2=an-1an+1(n≥2,n∈N+);
(2)通项公式:an=a1qn-1,an=amqn-m;
前n项和公式: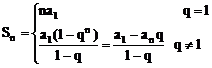 ;
;
(3)性质
当m+n=p+q时,aman=apaq,特例:a1an=a2an-1=a3an-2=…,当2n=p+q时,an2=apaq,数列{kan},{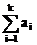 }成等比数列。
}成等比数列。
2、等差数列
(1)定义,{an}为等差数列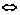 an+1-an=d(常数),n∈N+
an+1-an=d(常数),n∈N+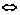 2an=an-1+an+1(n≥2,n∈N+);
2an=an-1+an+1(n≥2,n∈N+);
(2)通项公式:an=an+(n-1)d,an=am+(n-m)d;
前n项和公式: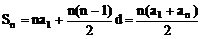 ;
;
(3)性质:an=an+b,即an是n的一次型函数,系数a为等差数列的公差;
Sn=an2+bn,即Sn是n的不含常数项的二次函数;
若{an},{bn}均为等差数列,则{an±nn},{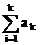 },{kan+c}(k,c为常数)均为等差数列;
},{kan+c}(k,c为常数)均为等差数列;
当m+n=p+q时,am+an=ap+aq,特例:a1+an=a2+an-1=a3+an-2=…;当2n=p+q时,2an=ap+aq;
当n为奇数时,S2n-1=(2n-1)an;S奇=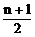 a中,S偶=
a中,S偶=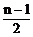 a中。
a中。
1、数列,是按照一定顺序排列而成的一列数,从函数角度看,这种顺序法则就是函数的对应法则,因此数列可以看作是一个特殊的函数,其特殊性在于:第一,定义域是正整数集或其子集;第二,值域是有顺序的,不能用集合符号表示。
研究数列,首先研究对应法则--通项公式:an=f(n),n∈N+,要能合理地由数列前n项写出通项公式,其次研究前n项和公式Sn:Sn=a1+a2+…an,由Sn定义,得到数列中的重要公式: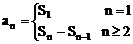 。
。
一般数列的an及Sn,,除化归为等差数列及等比数列外,求Sn还有下列基本题型:列项相消法,错位相消法。
2、一般数列的通项及前n项和计算。
1、等差数列及等比数列的定义,通项公式,前n项和公式及性质;
(三)解答题
14、已知y=2x是△ABC中∠C平分线所在直线方程,A(-4,2),B(3,1),求点C坐标,并判断△ABC形状。
15、已知n条直线:x-y+ci=0(i=1,2,…,n),其中C1=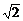 ,C1<C2<C3<…<Cn,且每相邻两条之间的距离顺次为2,3,4,…,n,(1)求Cn;(2)求x-y+Cn=0与坐标轴围成的三角形面积:(3)求x-y+Cn-1=0与x-y+Cn=0与x轴、y轴围成的图形面积。
,C1<C2<C3<…<Cn,且每相邻两条之间的距离顺次为2,3,4,…,n,(1)求Cn;(2)求x-y+Cn=0与坐标轴围成的三角形面积:(3)求x-y+Cn-1=0与x-y+Cn=0与x轴、y轴围成的图形面积。
16、已知与曲线C:x2+y2-2x-2y+1=0相切的直线l交x、y轴于A、B两点,O为原点,|OA|=a,|OB|=b,a>2,b>2,(1)求证:(a-2)(b-2)=2;(2)求线段AB中点的轨迹方程;(3)求△AOB面积的最小值。
17、已知两圆x2+y2=4和x2+(y-8)2=4,(1)若两圆分别在直线y=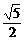 x+b两侧,求b取值范围;(2)求过点A(0,5)且和两圆都没有公共点的直线的斜率k的范围。
x+b两侧,求b取值范围;(2)求过点A(0,5)且和两圆都没有公共点的直线的斜率k的范围。
18、当0<a<2时,直线l1:ax-2y-2a+4=0与l2:2x+a2y-2a2-4=0和坐标轴成一个四边形,要使围成的四边形面积最小,a应取何值?
(二)填空题
9、直线ax+by+c=0与直线dx+ey+c=0的交点为(3,-2),则过点(a,b),(d,e)的直线方程是___________________。
10、已知{(x,y)|(m+3)x+y=3m-4}∩{(x,y)|7x+(5-m)y-8=0}=φ,则直线(m+3)x+y=
3m+4与坐标轴围成的三角形面积是__________________。
11、已知x,y满足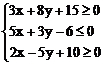 ,则x-y的最大值为________,最小值为________。
,则x-y的最大值为________,最小值为________。
12、过点A(2,1),且在坐标轴截距相等的直线方程是_________________。
13、已知圆:(x-1)2+y2=1,作弦OA,则OA中点的轨迹方程是__________________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com