
3、不等式的解法;
2、不等式的证明;
1、不等式的概念及性质;
(三)解答题
14、求以达原点与圆x2+y2-4x+3=0相切的两直线为渐近线且过椭圆4x2+y2=4两焦点的双曲线方程。
15、已知P(x,y)为平面上的动点且x≥0,若P到y轴距离比到点(1,0)距离小1
(1)求点P轨迹C的方程;
(2)设过M(m,0)的直线交双曲线C于A、B两点,问是否存在这样的m,使得以线段AB为直径的圆恒过原点。
16、设抛物线y2=4ax(a>0)的焦点为A,以B(a+4,0)为圆心,|BA|为半径,在x轴上方画圆,设抛物线与半圆交于不同两点M、N,点P是MN中点
(1)求|AM|+|AN|的值;
(2)是否存在这样的实数a,恰使|AM|,|AP|,|AN|成等差数列?若存在,求出a;若不存在,说明理由。
17、设椭圆中心为0,一个焦点F(0,1),长轴和短轴长度之比为t
(1)求椭圆方程;
(2)设过原点且斜率为t的直线与椭圆在y轴右边部分交点为Q,点P在该直线上,且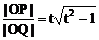 ,当t变化时,求点P轨迹。
,当t变化时,求点P轨迹。
18、已知抛物线y2=2px(p>0),过动点M(a,0)且斜率为1的直线l与该抛物线交于不同两点A、B,|AB|≤2p,
(1)求a取值范围;
(2)若线段AB垂直平分线交x同于点N,求△NAB面积的最大值。
(二)填空题
9、已知A(4,0),B(2,2)是椭圆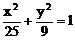 内的点,M是椭圆上的动点,则|MA|+|MB|的最大值是____________。
内的点,M是椭圆上的动点,则|MA|+|MB|的最大值是____________。
10、椭圆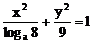 的离心率为
的离心率为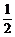 ,则a=__________。
,则a=__________。
11、高5米和3m的旗竿在水平地面上,如果把两旗竿底部的坐标分别定为A(-5,0),B(5,0),则地面上杆顶仰角相等的点的轨迹是__________。
12、若x,y∈R,且3x2+2y2=6,则x2+y2最大值是________,最小值是________。
13、抛物线y2=2x上到直线x-y+3=0距离最短的点的坐标为__________。
(一)选择题
1、方程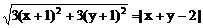 表示的曲线是
表示的曲线是
A、 椭圆 B、双曲线 C、抛物线 D、不能确定
2、把椭圆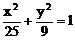 绕它的左焦点顺时针方向旋转
绕它的左焦点顺时针方向旋转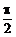 ,则所得新椭圆的准线方程是 A、
,则所得新椭圆的准线方程是 A、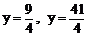 B、
B、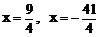
C、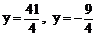 D、
D、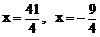
3、方程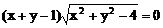 的曲线形状是
的曲线形状是
A、圆 B、直线 C、圆或直线 D、圆或两射线
4、F1、F2是椭圆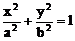 (a>b>0)的两焦点,过F1的弦AB与F2组成等腰直角三角形ABF2,其中∠BAF2=900,则椭圆的离心率是
(a>b>0)的两焦点,过F1的弦AB与F2组成等腰直角三角形ABF2,其中∠BAF2=900,则椭圆的离心率是
A、  B、
B、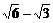 C、
C、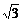 D、
D、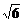
5、若方程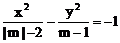 表示焦点在y轴上的双曲线,则它的半焦距C的取值范围是
表示焦点在y轴上的双曲线,则它的半焦距C的取值范围是
A、(0,1) B、(1,2) C、(1,+∞) D、与m有关
6、以抛物线y2=2px(p>0)的焦半径|PF|为直径的圆与y轴位置关系是
A、相交 B、相切 C、相离 D、以上三种均有可能
7、直线y=kx-2交抛物线y2=8x于A、B两点,若AB中点横坐标为2,则|AB|为
A、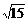 B、
B、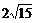 C、
C、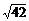 D、
D、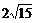
8、已知圆x2+y2=1,点A(1,0),△ABC内接于圆,∠BAC=600,当BC在圆上运动时,BC中点的轨迹方程是
A、x2+y2=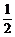 B、x2+y2=
B、x2+y2=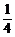
C、x2+y2=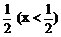 D、x2+y2=
D、x2+y2=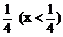
4、圆锥曲线中参数取值范围问题通常从两个途径思考,一是建立函数,用求值域的方法求范围;二是建立不等式,通过解不等式求范围。
3、直线和圆锥曲线位置关系
(1)位置关系判断:△法(△适用对象是二次方程,二次项系数不为0)。
其中直线和曲线只有一个公共点,包括直线和双曲线相切及直线与双曲线渐近线平行两种情形;后一种情形下,消元后关于x或y方程的二次项系数为0。
直线和抛物线只有一个公共点包括直线和抛物线相切及直线与抛物线对称轴平行等两种情况;后一种情形下,消元后关于x或y方程的二次项系数为0。
(2)直线和圆锥曲线相交时,交点坐标就是方程组的解。
当涉及到弦的中点时,通常有两种处理方法:一是韦达定理;二是点差法。
2、三种圆锥曲线的研究
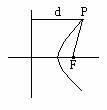 (1)统一定义,三种圆锥曲线均可看成是这样的点集:
(1)统一定义,三种圆锥曲线均可看成是这样的点集: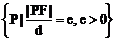 ,其中F为定点,d为P到定直线的l距离,F
,其中F为定点,d为P到定直线的l距离,F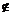 l,如图。
l,如图。
因为三者有统一定义,所以,它们的一些性质,研究它们的一些方法都具有规律性。
当0<e<1时,点P轨迹是椭圆;当e>1时,点P轨迹是双曲线;当e=1时,点P轨迹是抛物线。
(2)椭圆及双曲线几何定义:椭圆:{P||PF1|+|PF2|=2a,2a>|F1F2|>0,F1、F2为定点},双曲线{P|||PF1|-|PF2||=2a,|F1F2|>2a>0,F1,F2为定点}。
(3)圆锥曲线的几何性质:几何性质是圆锥曲线内在的,固有的性质,不因为位置的改变而改变。
①定性:焦点在与准线垂直的对称轴上
椭圆及双曲线中:中心为两焦点中点,两准线关于中心对称;椭圆及双曲线关于长轴、短轴或实轴、虚轴成轴对称,关于中心成中心对称。
②定量:
|
|
椭 圆 |
双 曲 线 |
抛 物 线 |
|
|
焦
距 |
2c |
|
||
|
长轴长 |
2a |
-- |
|
|
|
实轴长 |
-- |
2a |
|
|
|
短轴长 |
2b |
|
||
|
焦点到对应 准线距离 |
P=2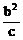 |
p |
||
|
通径长 |
2· |
2p |
||
|
离心率 |
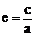 |
1 |
||
|
基本量关系 |
a2=b2+c2 |
C2=a2+b2 |
|
|
(4)圆锥曲线的标准方程及解析量(随坐标改变而变)
举焦点在x轴上的方程如下:
|
|
椭 圆 |
双 曲 线 |
抛 物 线 |
|
标准方程 |
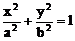 (a>b>0) |
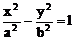 (a>0,b>0) |
y2=2px(p>0) |
|
顶
点 |
(±a,0) (0,±b) |
(±a,0) |
(0,0) |
|
焦
点 |
(±c,0) |
(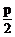 ,0) ,0) |
|
|
准
线 |
X=±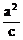 |
x=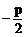 |
|
|
中
心 |
(0,0) |
|
|
|
有界性 |
|x|≤a |y|≤b |
|x|≥a |
x≥0 |
|
焦半径 |
P(x0,y0)为圆锥曲线上一点,F1、F2分别为左、右焦点 |
||
|
|PF1|=a+ex0 |PF2|=a-ex0 |
P在右支时: |PF1|=a+ex0 |PF2|=-a+ex0 P在左支时: |PF1|=-a-ex0 |PF2|=a-ex0 |
|PF|=x0+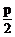 |
总之研究圆锥曲线,一要重视定义,这是学好圆锥曲线最重要的思想方法,二要数形结合,既熟练掌握方程组理论,又关注图形的几何性质,以简化运算。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com