
4.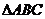 中,若
中,若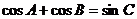 ,则
,则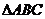 的形状是 ( )
的形状是 ( )
A.等腰三角形 B.等边三角形 C.等腰直角三角形 D.直角三角形
3.设函数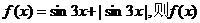 为 ( )
为 ( )
A.周期函数,最小正周期为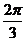 B.周期函数,最小正周期为
B.周期函数,最小正周期为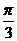
C.周期函数,数小正周期为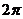 D.非周期函数
D.非周期函数
2.果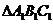 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于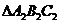 的三个内角的正弦值,则 ( )
的三个内角的正弦值,则 ( )
A.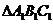 和
和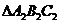 都是锐角三角形
都是锐角三角形
B.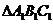 和
和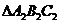 都是钝角三角形
都是钝角三角形
C.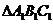 是钝角三角形,
是钝角三角形,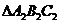 是锐角三角形
是锐角三角形
D.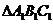 是锐角三角形,
是锐角三角形,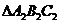 是钝角三角形
是钝角三角形
1.使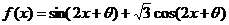 为奇函数,且在
为奇函数,且在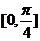 上是减函数的
上是减函数的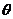 的一个值
的一个值
是 ( )
A.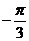 B.
B.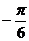 C.
C.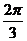 D.
D.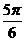
22.(14分)(理)在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2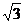 ,M、N分别为AB、SB的中点。
,M、N分别为AB、SB的中点。
(Ⅰ)证明:AC⊥SB;(Ⅱ)求二面角N-CM-B的大小;
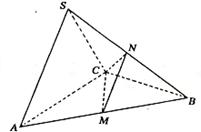 (Ⅲ)求点B到平面CMN的距离.
(Ⅲ)求点B到平面CMN的距离.
(文)如图,三定点A(2,1),B(0,-1),C(-2,1);三动点D,E,M满足= t, = t ,=t ,t∈[0,1].
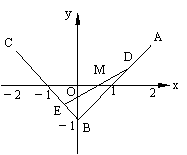 (Ⅰ)求动直线DE斜率的变化范围;
(Ⅰ)求动直线DE斜率的变化范围;
21.(12分)(理)在长方体ABCD-A1B1C1D1,中,AD=AA1=1,AB=2,点E在棱AD上移动.
(I)证明:D1E⊥A1D;
(II)当E为AB的中点时,求点E到面ACD1的距离;
(III)AE等于何值时,二面角D1-EC-D的大小为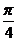 。
。
(文)已知两定点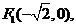
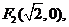 满足条件
满足条件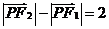 的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A、B两点。
的点P的轨迹是曲线E,直线y=kx-1与曲线E交于A、B两点。
(Ⅰ)求k的取值范围;
(Ⅱ)如果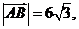 且曲线E上存在点C,使
且曲线E上存在点C,使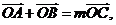 求中
求中 。
。
20.(12分)(理)如图9-6-6,矩形ABCD中,AB=1,BC= a,PA⊥平面ABCD
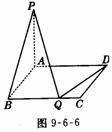 (Ⅰ)问BC边上是否存在Q点,使
(Ⅰ)问BC边上是否存在Q点,使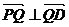 ,说明理由.
,说明理由.
(Ⅱ)问当Q点惟一,且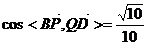 时,
时,
求点P的位置.
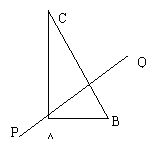
(文)如图,在Rt△ABC中,已知BC=a,若长为2a的线段PQ以点A为中点,问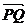 与
与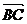 的夹角θ取何值时,
的夹角θ取何值时,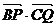 的值最大?并求出这个最大值。
的值最大?并求出这个最大值。
19.(12分)已知向量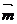 =(1,1),向量
=(1,1),向量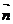 与向量
与向量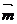 夹角为
夹角为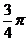 ,且
,且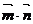 =-1.
=-1.
(Ⅰ)求向量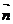 ;
;
(Ⅱ)若向量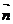 与向量
与向量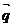 =(1,0)的夹角为
=(1,0)的夹角为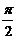 ,向量
,向量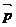 =
=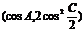 ,其中A、C为△ABC的内角,且A、B、C依次成等差数列. 求|
,其中A、C为△ABC的内角,且A、B、C依次成等差数列. 求|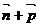 |的取值范围;
|的取值范围;
18.(12分)设向量 .
.
(Ⅰ)求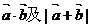 ;
;
(Ⅱ)若函数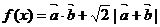 ,求
,求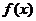 的最小值、最大值.
的最小值、最大值.
17.(12分)已知向量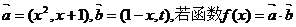 在区间(-1,1)上是增函数,求t的取值范围.
在区间(-1,1)上是增函数,求t的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com