2.下列四地的农业生产活动，合理的是

A.甲--育用材林　　　　　　　　　 B.乙--培育橡胶

C.丙--种植棉花　　　　　　　　　 D.丁--发展茶园

[解析]橡胶树对生长环境的要求极为严格，它是典型的热带雨林树种，喜高温、高湿、静风、沃土。目前，主要的橡胶产地是海南岛和云南的西双版纳。丙处等高线密集，坡度大，不能种植棉花，应当种植林木。甲处地势相对平坦，可以发展种植业。

[答案]D

1.图示区域内拥有且最突出的旅游资源是

A.瀑布飞流　　　　 B.湖光山色　　　 C.云海日出　　　 D.奇峰峡谷

[解析]图中的河流②、④在200米等高线处注入湖泊，湖泊周围是山脉。

[答案]B

22.(2008·南京模拟)(14分)已知函数y=f(x)是定义在区间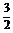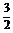［-，］上的偶函数，且x∈［0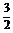，］时，f(x)=-x²-x+5.　

(1)求函数f(x)的解析式；　

(2)若矩形ABCD的顶点A，B在函数y=f(x)的图象上，顶点C，D在x轴上，求矩形ABCD面积的最大值.　

解　 (1)当x∈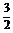［-，0］时，-x∈［0，］.　

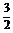∴f(-x)=-(-x)²-(-x)+5=-x²+x+5.又∵f(x)是偶函数，　

∴f(x)=f(-x)=-x²+x+5.　∴f(x)=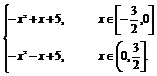　

(2)由题意，不妨设A点在第一象限，坐标为(t,-t²-t+5),其中t∈(0，］.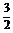　

由图象对称性可知B点坐标为(-t，-t²-t+5).则S(t)=S_矩形ABCD=2t(-t²-t+5)=-2t³-2t²+10t.　

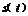=-6t²-4t+10.由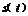=0，得t₁=-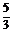(舍去)，t₂=1.当0＜t＜1时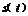，＞0;t＞1时,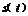＜0.　

　∴S(t)在(0，1］上单调递增，在［1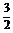，］上单调递减.∴当t=1时，矩形ABCD的面积取得极大值6，

且此极大值也是S(t)在t∈(0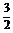，］上的最大值.从而当t=1时，矩形ABCD的面积取得最大值6.

21.(12分)已知定义域为R的函数f(x)满足f(f(x)-x²+x)=f(x)-x²+x.　

(1)若f(2)=3,求f(1);又若f(0)=a,求f(a);　

(2)设有且仅有一个实数x₀,使得f(x₀)=x₀,求函数f(x)解析表达式.　

解 (1)因为对任意x∈R,有f(f(x)-x²+x)=f(x)-x²+x,　

所以f(f(2)-2²+2)=f(2)-2²+2又由f(2)=3,得f(3-2²+2)=3-2²+2,即f(1)=1.　

若f(0)=a,则f(a-0²+0)=a-0²+0,即f(a)=a.　

(2)因为对任意x∈R,有f(f(x)-x²+x)=f(x)-x²+x.又因为有且只有一个实数x₀,使得f(x₀)=x₀.　

所以对任意x∈R,有f(x)-x²+x=x₀.在上式中令x=x₀,有f(x₀)-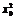+x₀=x₀.　

又因为f(x₀)=x₀,所以x₀-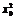=0,故x₀=0或x₀=1.若x₀=0,则f(x)-x²+x=0,即f(x)=x²-x.　

但方程x²-x=x有两个不同实根，与题设条件矛盾，故x₀≠0.　

若x₀=1，则有f(x)-x²+x=1,即f(x)=x²-x+1.易验证该函数满足题设条件.　

20.(12分)设a,b∈R，且a≠2,定义在区间(-b,b)内的函数f(x)=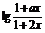是奇函数.　

(1)求b的取值范围；　

(2)讨论函数f(x)的单调性.　

解 (1)f(x)=lg 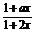(-b＜x＜b)是奇函数等价于：　

对任意x∈(-b,b)都有　

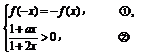①式即为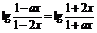，由此可得　

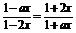,也即a²x²=4x²,此式对任意x∈(-b,b)都成立相当于a²=4,因为a≠2,所以a=-2，

代入②式，得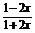＞0,即-＜x＜,此式对任意x∈(-b,b)都成立相当于-≤-b＜b≤,　

所以b的取值范围是(0, ］.　

(2)设任意的x₁,x₂∈(-b,b)，且x₁＜x₂,由b∈(0，］，得-≤-b＜x₁＜x₂＜b≤,　

所以0＜1-2x₂＜1-2x₁,0＜1+2x₁＜1+2x₂,　

从而f(x₂)-f(x₁)=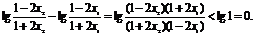

因此f(x)在(-b,b)内是减函数，具有单调性.

19.(2008·深圳模拟)(12分)据调查，某地区100万从事传统农业的农民，人均收入3 000元，为了增加农民的收入，当地政府积极引进资本，建立各种加工企业，对当地的农产品进行深加工，同时吸收当地部分农民进入加工企业工作，据估计，如果有x (x＞0)万人进企业工作，那么剩下从事传统农业的农民的人均收入有望提高2x%,而进入企业工作的农民的人均收入为3 000a元 (a＞0).　

(1)在建立加工企业后，要使从事传统农业的农民的年总收入不低于加工企业建立前的农民的年总收入，试求x的取值范围；　

(2)在(1)的条件下，当地政府应该如何引导农民(即x多大时)，能使这100万农民的人均年收入达到最大.　

解(1)由题意得　

(100-x)·3 000·(1+2x%)≥100×3 000,即x²-50x≤0,解得0≤x≤50.　

又∵x＞0,∴0＜x≤50.　

(2)设这100万农民的人均年收入为y元,　

则y=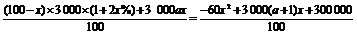

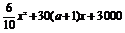=-.∴若25(a+1)≤50,即0＜a≤1时，当x=25(a+1)时，

y_max=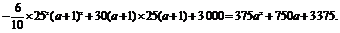

若a＞1时，函数在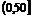上是增函数. ∴当x=50时，

y_max=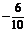×50²+30(a+1)×50+3 000=-1 500+1 500a+1 500+3 000=1 500a+3 000.

答 若0＜a≤1,当x=25(a+1)时,使100万农民人均年收入最大.　

若a＞1,当x=50时,使100万农民的人均年收入最大.　

18.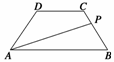(12分)等腰梯形ABCD的两底分别为AB=10，CD=4，两腰AD=CB=5，动点P由B点沿折线BCDA向A运动，设P点所经过的路程为x，三角形ABP的面积为S　

(1)求函数S=f(x)的解析式；　

(2)试确定点P的位置，使△ABP的面积S最大.　

解 (1)过C点作CE⊥AB于E，　

在△BEC中，CE=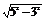=4，∴sinB=.　

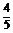由题意，当x∈(0，5］时，过P点作PF⊥AB于F，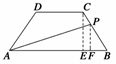　

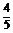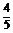∴PF=xsinB=x，∴S=×10×x=4x,　

当x∈(5，9］时，∴S=×10×4=20.　

当x∈(9，14］时，AP=14-x，PF=AP·sinA=，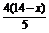　

∴S=×10×(14-x) ×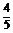=56-4x.综上可知,函数S=f(x)=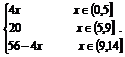

(2)由(1)知,当x∈(0,5］时,f(x)=4x为增函数,所以,当x=5时,取得最大值20.　

当x∈(5,9］时,f(x)=20,最大值为20.当x∈(9,14］时,f(x)=56-4x为减函数,无最大值.　

综上可知:当P点在CD上时,△ABP的面积S最大为20.

17.(12分)设直线x=1是函数f(x)的图象的一条对称轴，对于任意x∈R，f(x+2)=-f(x),当-1≤x≤1时，f(x)=x³.

(1)证明：f(x)是奇函数；　

(2)当x∈［3，7］时，求函数f(x)的解析式.　

(1)证明　 ∵x=1是f(x)的图象的一条对称轴，　

∴f(x+2)=f(-x).又∵f(x+2)=-f(x),　

∴f(x)=-f(x+2)=-f(-x),即f(-x)=-f(x).∴f(x)是奇函数.　

(2)解　 ∵f(x+2)=-f(x)，∴f(x+4)=f［(x+2)+2］　

=-f(x+2)=f(x)，∴T=4.若x∈［3，5］，则(x-4)∈［-1，1］，　

∴f(x-4)=(x-4)³.又∵f(x-4)=f(x),　

∴f(x)=(x-4)³,x∈［3，5］.若x∈(5，7］，则(x-4)∈(1，3］，f(x-4)=f(x).　

由x=1是f(x)的图象的一条对称轴可知f［2-(x-4)］=f(x-4)　

且2-(x-4)=(6-x)∈［-1，1］，故f(x)=f(x-4)=f(6-x)=(6-x)³=-(x-6)³.　

综上可知f(x)=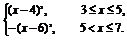

16.(2008·福州模拟)对于函数f(x)定义域中任意的x₁,x₂ (x₁≠x₂),　

有如下结论：　

①f(x₁+x₂)=f(x₁)f(x₂);　

②f(x₁·x₂)=f(x₁)+f(x₂);　

③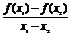＞0;　

④f()＜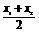

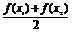
当f(x)=2^x时，上述结论中正确结论的序号是　　　　　 .　

答案　 ①③④　

15.(2008·通州模拟)用二分法求方程x³-2x-5=0在区间［2，3］内的实根，取区间中点x₀=2.5,那么下一个有实根的区间是　　　 .　

答案 (2，2.5)