3.已知光线每通过一块玻璃板，光线的强度要损失10%，要使通过玻璃板的光线的强度减弱到原来强度的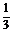以下，则至少需要重叠玻璃板数为　　　　　　　　　　　　　　　　　　　　　　 　　　(　 )　

A.8块　　 　　　　　　　B.9块　　　　　　　 C.10块　　　　　　　 D.11块　

答案?D?　

2.我国为了加强对烟酒生产的宏观调控，除了应征税外还要征收附加税，已知某种酒每瓶售价为70元，不收附加税时，每年大约销售100万瓶，若每销售100元国家要征附加税为x元(税率x%)，则每年销售量减少10x 万瓶，为了要使每年在此项经营中收取的附加税额不少于112万元，则x的最小值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　(　 )

A.2　　　　　　　 　　 　B.6 　　　　　　　　　C.8　　　　　　　　　　 D.10　

答案?A?　

1.一等腰三角形的周长是20，底边y是关于腰长x的函数，它的解析式为　　　　　　　 　　(　 )　

A.y=20-2x (x≤10)　　　　　　　　　　　　　 B.y=20-2x (x＜10)　

C.y=20-2x (5≤x≤10)?　　　　　　　　　　　 D.y=20-2x (5＜x＜10)　

答案?D?　

12.已知函数f(x)=2^x+1，将函数y=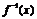的图象向左平移2个单位，再向上平移1个单位，就得到y=g(x)的图象.

(1)写出y=g(x)的解析式；　

(2)求出F(x)=g(x²)-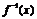的最小值及取得最小值时x的值.　

解(1)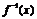=log₂x-1,　

则向左平移2个单位，再向上平移1个单位，得y=log₂(x+2)-1+1=log₂(x+2)(x＞-2),　

∴g(x)=log₂(x+2)(x＞-2).　

(2)F(x)=log₂(x²+2)-(log₂x-1) (x＞0)=log₂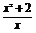+1≥log₂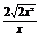+1=,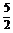　

当且仅当x²=2且x＞0,∴当x=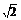时，F(x)_min=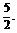

§2.9　 函数模型及其应用

基础自测

11.(1)已知函数y=f(x)的定义域为R，且当x∈R时f(m+x)=f(m-x)恒成立.

求证：y=f(x)的图象关于直线x=m对称；　

(2)若函数y=log₂|ax-1|的图象的对称轴是x=2,求非零实数a的值.　

(1)证明 设P(x₀,y₀)是y=f(x)图象上任意一点，则y₀=f(x₀).又设P点关于x=m的对称点为P′，则P′的

坐标为(2m-x₀,y₀).　

由已知f(m+x)=f(m-x),　

得f(2m-x₀)=f［m+(m-x₀)］=f［m-(m-x₀)］　

=f(x₀)=y₀.

即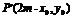在y=f(x)图象上，　

∴y=f(x)的图象关于直线x=m对称.　

(2)解 ∵对定义域内的任意x,有f(2-x)=f(2+x)恒成立.　

∴|a(2-x)-1|=|a(2+x)-1|恒成立，　

即|-ax+(2a-1)|=|ax+(2a-1)|恒成立.　

又a≠0,∴2a-1=0,得a=.

10.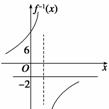已知函数f(x)=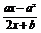(a≠0)的反函数的图象如图所示，求a、b的值并写出f ^-1(x)的解析式.　

解 由图象知f ^-1(x)的图象过点(0，6).　

所以f(x)的图象必过点(6，0)，　

得到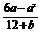=0.　

解得a=6或a=0(舍去).所以f(x)=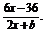又由图象知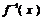的值域为{y|y≠-2}.　

即函数f(x)的定义域为{x|x≠-2},　

又f(x)= 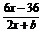的定义域为,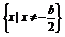　

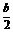∴-=-2,∴b=4.　

∴f(x)==.∴=.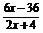

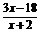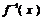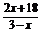9.设函数f(x)=x²-2|x|-1 (-3≤x≤3).　

(1)证明：f(x)是偶函数；　

(2)画出函数的图象；　

(3)指出函数f(x)的单调区间，并说明在各个单调区间上f(x)是增函数还是减函数；　

(4)求函数的值域.　

(1)证明 　f(-x)=(-x)²-2|-x|-1　

=x²-2|x|-1=f(x),　

即f(-x)=f(x),∴f(x)是偶函数.　

(2)解 当x≥0时，f(x)=x²-2x-1=(x-1)²-2,　

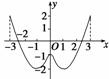当x＜0时，f(x)=x²+2x-1=(x+1)²-2,　

即f(x)=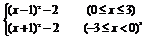

根据二次函数的作图方法，可得函数图象如图所示.　

(3)解 函数f(x)的单调区间为［-3，-1)，［-1，0)，［0，1)，［1，3］.

f(x)在区间［-3，-1)和［0，1)上为减函数，在［-1，0)，［1，3］上为增函数.　

(4)解 当x≥0时，函数f(x)=(x-1)²-2的最小值为-2,最大值为f(3)=2;　

当x＜0时，函数f(x)=(x+1)²-2的最小值为-2,　

最大值为f(-3)=2;　

故函数f(x)的值域为［-2，2］.

8.设f(x)是定义在R上的奇函数，在(0，)上单调递减，且f(x)=f(-x-1).给出下列四个结论：　

①函数f(x)的图象关于直线x=对称；②f(x)在(,1)上单调递增；③对任意的x∈Z，都有f(x)=0；

④函数y=f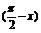的图象是中心对称图形，且对称中心为(.　

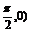其中正确命题的序号是　　　　　　　 .　

答案　 ①②③④　

7.使log₂(-x)＜x+1成立的x的取值范围是　　　　　 .　

答案 (-1，0)　

6.(2008·安徽理，9)在同一平面直角坐标系中，函数y=g(x)的图象与y=e^x的图象关于直线y=x对称，而函数y=f(x)的图象与y=g(x)的图象关于y轴对称，若f(m)=-1，则m的值为　　　　 (　 )　?A.-e　　　　　　　　　　　 B.-?　　　　 　　　　　　C.e??　　　　　　　　　 D.　

答案?B?