
1. 设abc≠0,“ac>0”是“曲线ax2+by2=c为椭圆”的 ( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分又不必要条件
6. 向量的坐标形式及应用是解析法的重要补充,应注意把二者有机地结合起来
[模拟试题](满分100分,时间60分钟)
5. 求出轨迹方程后要注意检验,以保证方程的解与曲线上的点具有一一对应的关系,尤其是题中涉及三角形、斜率、参数方程中参数的限制,往往使方程产生增根
4. 求轨迹方程的主要方法有:直接法、定义法、代入法、参数法
3. 注意用好以下数学思想、方法:
①方程思想;②函数思想;③对称思想;④参数思想;⑤转化思想;⑥分类思想
除上述几种常用数学思想外,整体思想、数形结合思想、主元分析思想、正难则反思想、构造思想等也是解析几何解题中不可缺少的思想方法 在学习中必须给予足够的重视,真正发挥数学解题思想作为联系知识与能力中的作用,从而提高简化计算能力
在学习中必须给予足够的重视,真正发挥数学解题思想作为联系知识与能力中的作用,从而提高简化计算能力
2. 四点重视:①重视定义在解题中的作用;②重视平面几何知识在解题中的简化功能;③重视根与系数关系在解题中的作用;④重视曲线的几何特征与方程的代数特征的统一
解析几何是联系初等数学与高等数学的纽带,它本身侧重于形象思维、推理运算和数形结合,综合了代数、三角、几何、向量等知识 反映在解题上,就是根据曲线的几何特征准确地转换为代数形式,根据方程画出图形,研究几何性质
反映在解题上,就是根据曲线的几何特征准确地转换为代数形式,根据方程画出图形,研究几何性质 学习时应熟练掌握函数与方程的思想、数形结合的思想、参数的思想、分类与转化的思想等,以达到优化解题的目的
学习时应熟练掌握函数与方程的思想、数形结合的思想、参数的思想、分类与转化的思想等,以达到优化解题的目的
具体来说,有以下三方面:
(1)确定曲线方程,实质是求某几何量的值;含参数系数的曲线方程或变化运动中的圆锥曲线的主要问题是定值、最值、最值范围问题,这些问题的求解都离不开函数、方程、不等式的解题思想方法 有时题设设计的非常隐蔽,这就要求认真审题,挖掘题目的隐含条件作为解题突破口
有时题设设计的非常隐蔽,这就要求认真审题,挖掘题目的隐含条件作为解题突破口
(2)解析几何也可以与数学其他知识相联系,这种综合一般比较直观,在解题时保持思维的灵活性和多面性,能够顺利进行转化,即从一知识转化为另一知识
(3)解析几何与其他学科或实际问题的综合,主要体现在用解析几何知识去解有关知识,具体地说就是通过建立坐标系,建立所研究曲线的方程,并通过方程求解来回答实际问题 在这一类问题中“实际量”与“数学量”的转化是易出错的地方,这是因为在坐标系中的量是“数量”,不仅有大小还有符号
在这一类问题中“实际量”与“数学量”的转化是易出错的地方,这是因为在坐标系中的量是“数量”,不仅有大小还有符号
[典型例题]
例1 如图,O为坐标原点,直线l在x轴和y轴上的截距分别是a和b(a>0,b≠0),且交抛物线y2=2px(p>0)于M(x1,y1),N(x2,y2)两点
(1)写出直线l的截距式方程;
(2)证明: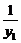 +
+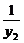 =
=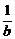 ;
;
(3)当a=2p时,求∠MON的大小
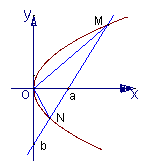
分析:易知直线l的方程为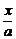 +
+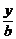 =1,欲证
=1,欲证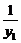 +
+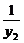 =
=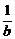 ,即求
,即求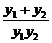 的值,为此只需求直线l与抛物线y2=2px交点的纵坐标
的值,为此只需求直线l与抛物线y2=2px交点的纵坐标 由根与系数的关系易得y1+y2、y1y2的值,进而证得
由根与系数的关系易得y1+y2、y1y2的值,进而证得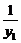 +
+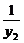 =
=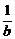
 由
由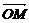 ·
·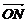 =0易得∠MON=90°
=0易得∠MON=90° 亦可由kOM·kON=-1求得∠MON=90°
亦可由kOM·kON=-1求得∠MON=90°
(1)解:直线l的截距式方程为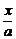 +
+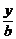 =1
=1
(2)证明:由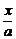 +
+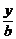 =1及y2=2px消去x可得by2+2pay-2pab=0
=1及y2=2px消去x可得by2+2pay-2pab=0
点M、N的纵坐标为y1、y2,
故y1+y2=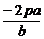 ,y1y2=-2pa
,y1y2=-2pa
所以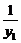 +
+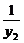 =
=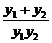 =
=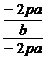 =
=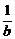

(3)解:设直线OM、ON的斜率分别为k1、k2,
则k1=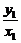 ,k2=
,k2=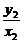

当a=2p时,由(2)知,y1y2=-2pa=-4p2,
由y12=2px1,y22=2px2,相乘得(y1y2)2=4p2x1x2,
x1x2=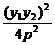 =
=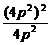 =4p2,
=4p2,
因此k1k2=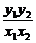 =
=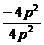 =-1
=-1
所以OM⊥ON,即∠MON=90°
点评:本题主要考查直线、抛物线等基本知识,考查运用解析几何的方法分析问题和解决问题的能力
例2 已知椭圆C的方程为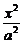 +
+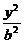 =1(a>b>0),双曲线
=1(a>b>0),双曲线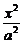 -
-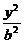 =1的两条渐近线为l1、l2,过椭圆C的右焦点F作直线l,使l⊥l1,又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B
=1的两条渐近线为l1、l2,过椭圆C的右焦点F作直线l,使l⊥l1,又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B (如图)
(如图)
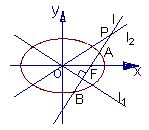
(1)当l1与l2夹角为60°,双曲线的焦距为4时,求椭圆C的方程;
(2)当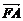 =λ
=λ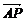 时,求λ的最大值
时,求λ的最大值
分析:(1)求椭圆方程即求a、b的值,由l1与l2的夹角为60°易得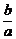 =
=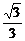 ,由双曲线的焦距为4易得a2+b2=4,进而可求得a、b
,由双曲线的焦距为4易得a2+b2=4,进而可求得a、b
(2)由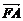 =λ
=λ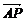 ,欲求λ的最大值,需求A、P的坐标,而P是l与l1的交点,故需求l的方程
,欲求λ的最大值,需求A、P的坐标,而P是l与l1的交点,故需求l的方程 将l与l2的方程联立可求得P点的坐标,进而可求得点A的坐标
将l与l2的方程联立可求得P点的坐标,进而可求得点A的坐标 将点A的坐标代入椭圆方程可求得λ的最大值
将点A的坐标代入椭圆方程可求得λ的最大值
解:(1)∵双曲线的渐近线为y=±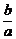 x,两渐近线夹角为60°,
x,两渐近线夹角为60°,
又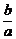 <1,∴∠POx=30°,即
<1,∴∠POx=30°,即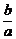 =tan30°=
=tan30°=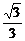
 ∴a=
∴a=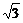 b
b
又a2+b2=4, ∴a2=3,b2=1
故椭圆C的方程为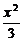 +y2=1
+y2=1
(2)由已知l:y=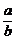 (x-c),与y=
(x-c),与y=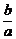 x解得P(
x解得P(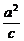 ,
,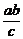 ),
),
由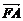 =λ
=λ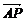 得A(
得A(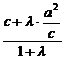 ,
,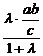 )
)
将A点坐标代入椭圆方程得
(c2+λa2)2+λ2a4=(1+λ)2a2c2
∴(e2+λ)2+λ2=e2(1+λ)2
∴λ2=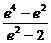 =-[(2-e2)+
=-[(2-e2)+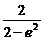 ]+3≤3-2
]+3≤3-2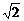

∴λ的最大值为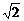 -1
-1
点评:本题考查了椭圆、双曲线的基础知识,及向量、定比分点公式、重要不等式的应用 解决本题的难点是通过恒等变形,利用重要不等式解决问题的思想
解决本题的难点是通过恒等变形,利用重要不等式解决问题的思想 本题是培养学生分析问题和解决问题能力的一道好题
本题是培养学生分析问题和解决问题能力的一道好题
例3 设椭圆中心是坐标原点,长轴在x轴上,离心率e=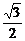 ,已知点P(0,
,已知点P(0,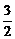 )到这个椭圆上的点的最远距离是
)到这个椭圆上的点的最远距离是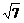 ,求这个椭圆方程,并求椭圆上到点P的距离等于
,求这个椭圆方程,并求椭圆上到点P的距离等于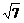 的点的坐标
的点的坐标
分析:设椭圆方程为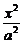 +
+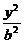 =1,由e=
=1,由e=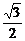 知椭圆方程可化为x2+4y2=4b2,然后将距离转化为y的二次函数,二次函数中含有一个参数b,在判定距离有最大值的过程中,要讨论y=-
知椭圆方程可化为x2+4y2=4b2,然后将距离转化为y的二次函数,二次函数中含有一个参数b,在判定距离有最大值的过程中,要讨论y=-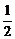 是否在y的取值范围内,最后求出椭圆方程和P点坐标
是否在y的取值范围内,最后求出椭圆方程和P点坐标
解法一:设所求椭圆的直角坐标方程是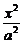 +
+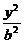 =1,其中a>b>0待定
=1,其中a>b>0待定
由e2=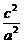 =
=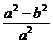 =1-(
=1-(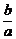 )2
)2
可知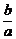 =
=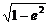 =
=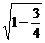 =
=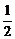 ,即a=2b
,即a=2b
设椭圆上的点(x,y)到点P的距离为d,
则d2=x2+(y-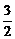 )2=a2(1-
)2=a2(1-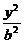 )+y2-3y+
)+y2-3y+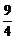
= 4b2-3y2-3y+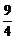 =-3(y+
=-3(y+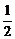 )2+4b2+3,其中-b≤y≤b
)2+4b2+3,其中-b≤y≤b
如果b<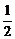 ,则当y=-b时d2(从而d)有最大值,
,则当y=-b时d2(从而d)有最大值,
由题设得(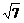 )2=(b+
)2=(b+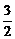 )2,
)2,
由此得b=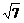 -
-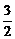 >
>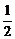 ,与b<
,与b<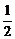 矛盾
矛盾
因此必有b≥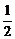 成立,于是当y=-
成立,于是当y=-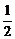 时d2(从而d)有最大值,
时d2(从而d)有最大值,
由题设得(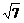 )2=4b2+3,由此可得b=1,a=2
)2=4b2+3,由此可得b=1,a=2
故所求椭圆的直角坐标方程是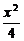 +y2=1
+y2=1
由y=-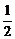 及求得的椭圆方程可得,椭圆上的点(-
及求得的椭圆方程可得,椭圆上的点(-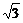 ,-
,-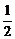 ),点(
),点(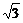 ,-
,-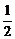 )到点P的距离都是
)到点P的距离都是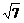

解法二:根据题设条件,设椭圆上任意一点的坐标为(x,y)则
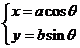 其中a>b>0待定,0≤θ<2π,
其中a>b>0待定,0≤θ<2π,
∵e=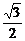 ,∴a=2b
,∴a=2b
设椭圆上的点(x,y)到点P的距离为d,则
d2=x2+(y-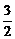 )2=a2cos2θ+(bsinθ-
)2=a2cos2θ+(bsinθ-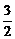 )2=-3b2·(sinθ+
)2=-3b2·(sinθ+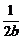 )2+4b2+3
)2+4b2+3
如果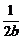 >1,即b<
>1,即b<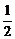 ,
,
则当sinθ=-1时,d2(从而d)有最大值,
由题设得(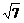 )2=(b+
)2=(b+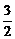 ) 2,
) 2,
由此得b=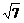 -
-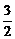 >
>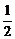 ,与b<
,与b<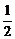 矛盾
矛盾
因此必有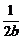 ≤1成立,于是当sinθ=-
≤1成立,于是当sinθ=-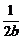 时,d2(从而d)有最大值,
时,d2(从而d)有最大值,
由题设得(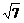 )2=4b2+3
)2=4b2+3 由此得b=1,a=2
由此得b=1,a=2
所以椭圆参数方程为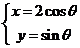
消去参数得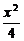 +y2=1,
+y2=1,
由sinθ=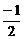 ,cosθ=±
,cosθ=±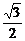 知椭圆上的点(-
知椭圆上的点(-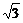 ,-
,-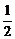 ),(
),(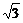 ,-
,-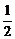 )到P点的距离都是
)到P点的距离都是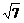

点评:本题体现了解析几何与函数、三角知识的横向联系,解答中要注意讨论
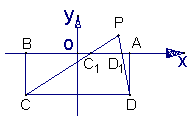
例4 如图,矩形ABCD中,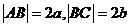 ,以AB边所在的直线为x轴,AB的中点为原点建立直角坐标系,P是x轴上方一点,使PC、PD与线段AB分别交于
,以AB边所在的直线为x轴,AB的中点为原点建立直角坐标系,P是x轴上方一点,使PC、PD与线段AB分别交于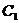 、
、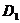 两点,且
两点,且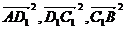 成等比数列,求动点P的轨迹方程
成等比数列,求动点P的轨迹方程
解:显然有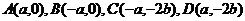 ,
,
设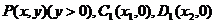 ,
,
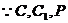 三点共线,
三点共线,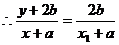 ,
,
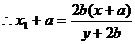 ,又
,又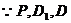 三点共线,
三点共线,
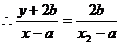 ,
,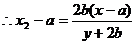 ,
,
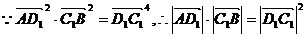 ,
,
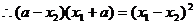 ,
,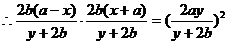 ,
,
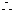 化简得动点P的轨迹方程为
化简得动点P的轨迹方程为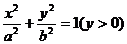

例5 设双曲线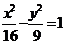 的两个焦点分别是F1和F2,A 、B分别是双曲线两条渐进线上的动点,且
的两个焦点分别是F1和F2,A 、B分别是双曲线两条渐进线上的动点,且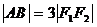 ,求线段AB中点的轨迹方程
,求线段AB中点的轨迹方程
分析:复习双曲线性质,注意点在直线上使横纵坐标互相转换
解:设A点在渐进线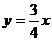 上,B点在渐进线
上,B点在渐进线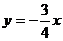 上,
上,
A(x1,y1),B(x2,y2),线段AB中点 M(x,y),
由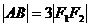 =30,得:
=30,得: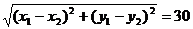 ,
,
又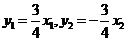 ,
,
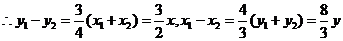
代入上式得: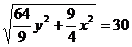 ,化简得:
,化简得: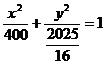
小结:
解析几何与函数、三角、数列、向量等知识联系密切,正是考查综合能力的地方。为此在学习时应抓住以下几点:
1. 客观题求解时应注意画图,抓住涉及到的一些元素的几何意义,用数形结合法去分析解决
教学重点:
掌握椭圆的定义、标准方程和椭圆的简单几何性质,理解椭圆的参数方程 (2)掌握双曲线的定义、标准方程和双曲线的简单几何性质
(2)掌握双曲线的定义、标准方程和双曲线的简单几何性质 (3)掌握抛物线的定义、标准方程和抛物线的简单几何性质
(3)掌握抛物线的定义、标准方程和抛物线的简单几何性质 (4)了解圆锥曲线的初步应用
(4)了解圆锥曲线的初步应用
教学难点:
解析几何知识的综合运用,以及与其它知识的灵活运用。
圆锥曲线的综合问题
22.甲、乙两袋均装有标有数字1、2、3、4、5的大小相同的小球各一个,从甲袋中任取1个小球,从乙袋中任取2个小球,用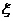 表示取出的3个小球上的最小数字。
表示取出的3个小球上的最小数字。
求:(1)取出的3个小球上的数字互不相同的概率;
(2)求P(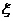 =2或
=2或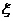 =3)的值
=3)的值
 江西省丰城中学高二年级第五次月考
江西省丰城中学高二年级第五次月考
|
座位号 |
|
|
|
|
数学试题 (理科零班卷) 2009.3.14
命题人:熊海荣 审题人:黄汉乐
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com