
6.同角三角函数的基本关系: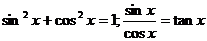 ;
;
5.⑴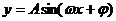 对称轴:
对称轴: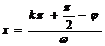 ;对称中心:
;对称中心: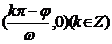 ;
;
⑵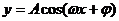 对称轴:
对称轴: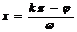 ;对称中心:
;对称中心: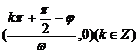 ;
;
4.诱导公式记忆规律:“函数名不(改)变,符号看象限”;
3.三角函数符号规律:一全正,二正弦,三两切,四余弦;
2.三角函数定义:角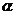 中边上任意一点
中边上任意一点 为
为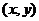 ,设
,设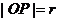 则:
则:
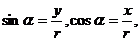
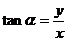
1.⑴角度制与弧度制的互化: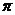 弧度
弧度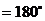 ,
,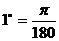 弧度,
弧度,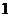 弧度
弧度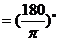
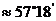
⑵弧长公式: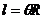 ;扇形面积公式:
;扇形面积公式: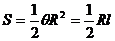 。
。
13.导数 ⑴导数定义:f(x)在点x0处的导数记作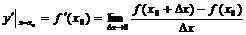 ;
;
⑵常见函数的导数公式: ①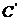
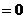 ;②
;②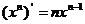 ;③
;③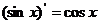 ;
;
④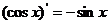 ;⑤
;⑤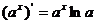 ;⑥
;⑥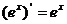 ;⑦
;⑦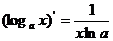 ;
;
⑧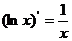 。⑶导数的四则运算法则:
。⑶导数的四则运算法则: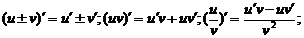
⑷(理科)复合函数的导数: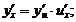
⑸导数的应用:①利用导数求切线:注意:ⅰ所给点是切点吗?ⅱ所求的是“在”还是“过”该点的切线?②利用导数判断函数单调性:ⅰ 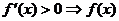 是增函数;
是增函数;
ⅱ 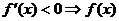 为减函数;ⅲ
为减函数;ⅲ 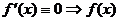 为常数;
为常数;
③利用导数求极值:ⅰ求导数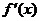 ;ⅱ求方程
;ⅱ求方程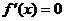 的根;ⅲ列表得极值。
的根;ⅲ列表得极值。
④利用导数最大值与最小值:ⅰ求的极值;ⅱ求区间端点值(如果有);ⅲ得最值。
14.(理科)定积分
⑴定积分的定义: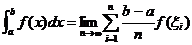
⑵定积分的性质:①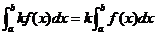 (
(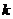 常数);
常数);
②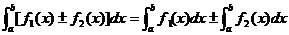 ;
;
③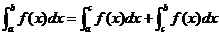 (其中
(其中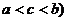 。
。
⑶微积分基本定理(牛顿-莱布尼兹公式):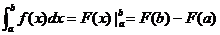
⑷定积分的应用:①求曲边梯形的面积: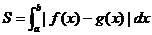 ;
;
①
求变速直线运动的路程: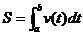 ;③求变力做功:
;③求变力做功: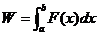 。
。
12.函数零点的求法:⑴直接法(求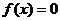 的根);⑵图象法;⑶二分法.
的根);⑵图象法;⑶二分法.
11.函数图象(曲线)对称性的证明
(1)证明函数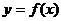 图像的对称性,即证明图像上任意点关于对称中心(对称轴)的对称点仍在图像上;
图像的对称性,即证明图像上任意点关于对称中心(对称轴)的对称点仍在图像上;
(2)证明函数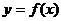 与
与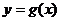 图象的对称性,即证明
图象的对称性,即证明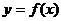 图象上任意点关于对称中心(对称轴)的对称点在
图象上任意点关于对称中心(对称轴)的对称点在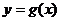 的图象上,反之亦然;
的图象上,反之亦然;
注:①曲线C1:f(x,y)=0关于点(a,b)的对称曲线C2方程为:f(2a-x,2b-y)=0;
②曲线C1:f(x,y)=0关于直线x=a的对称曲线C2方程为:f(2a-x, y)=0;
③曲线C1:f(x,y)=0,关于y=x+a(或y=-x+a)的对称曲线C2的方程为f(y-a,x+a)=0(或f(-y+a,-x+a)=0);④f(a+x)=f(b-x)
(x∈R) y=f(x)图像关于直线x=
y=f(x)图像关于直线x=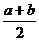 对称;
对称;
特别地:f(a+x)=f(a-x) (x∈R) y=f(x)图像关于直线x=a对称;
y=f(x)图像关于直线x=a对称;
⑤函数y=f(x-a)与y=f(b-x)的图像关于直线x=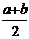 对称;
对称;
10.函数图象⑴图象作法 :①描点法(注意三角函数的五点作图)②图象变换法③导数法
⑵图象变换:
① 平移变换:ⅰ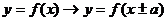 ,
,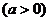 ---左“+”右“-”;
---左“+”右“-”;
ⅱ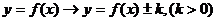 ---上“+”下“-”;
---上“+”下“-”;
② 伸缩变换:
ⅰ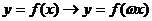 , (
, (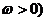 ---纵坐标不变,横坐标伸长为原来的
---纵坐标不变,横坐标伸长为原来的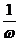 倍;
倍;
ⅱ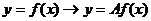 , (
, (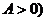 ---横坐标不变,纵坐标伸长为原来的
---横坐标不变,纵坐标伸长为原来的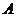 倍;
倍;
③ 对称变换:ⅰ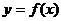
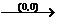
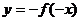 ;ⅱ
;ⅱ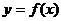
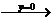
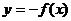 ;
;
ⅲ 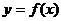
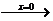
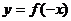 ; ⅳ
; ⅳ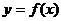
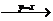
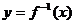 ;
;
④ 翻转变换:
ⅰ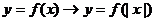 ---右不动,右向左翻(
---右不动,右向左翻(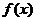 在
在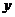 左侧图象去掉);
左侧图象去掉);
ⅱ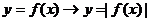 ---上不动,下向上翻(|
---上不动,下向上翻(|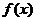 |在
|在 下面无图象);
下面无图象);
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com