11．若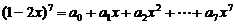,则　　　　 ,

　 　,　 　,　 　.

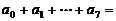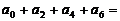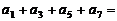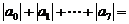10．求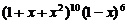展开式中各项系数的和.

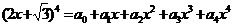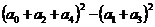9.若,则的值为

A.1　　　　　　 B.－1　　　　　　 C.0　　　　 　　D.2

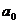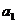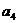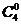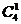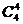
解：题中的，，…，是二项展开式的各项系数而不是各项的二项式系数，它们不等于，，…，令x＝1或－1可得它们的不同形式的代数和，于是可得结论答案选A.

8.在代数式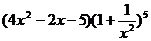的展开式中，常数项为_____.(答案:15)

7.用1、2、3、4、5、6六个数字组成没有重复数字的四位数中，是9的倍数的共有(　 　)

A.360个　　　 B.180个　　　　 C.120个　　　　 D.24个

解：因为3+4+5+6=18能被9整除，所以共有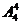=24个.

6.已知碳元素有3种同位素¹²C、¹³C、¹⁴C，氧元素也有3种同位素¹⁶O、¹⁷O、¹⁸O，则不同的原子构成的CO₂分子有(　 )

A.81种　　　　 B.54种　　　　　 C.27种　　　　 D.9种

解：分步计数原理，先选碳原子，再选第一个氧原子，第二个氧原子.所以

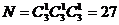(种)

5. 四面体的顶点和各棱中点共10个点，在其中取4个不共面的点，不同的取法有________种.

解：取出的4点不共面比取出的4点共面的情形要复杂，因此宜用间接法：用任意取出四点的组合总数减去这四点共面的取法数.取出四点共面时有三种可能第一类：四点共面于四面体的某一个面时，有4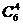种取法；第二类：由四面体的一条棱上三点及对棱中点所确定的平面有6个；第三类：过四面体中的四条棱的中点，而与另外两条棱平行的平面有3个.故取4个点不共面时的不同取法有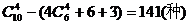

4.　 从5男4女中选4位代表，其中至少有2位男同志，且至少有1位女同志，分别到4个不同的工厂调查，不同的分派方法有(　 )

A.100种　　　 B.400种　　　 C.480种　　　 D.2400种

解：分两种情况，采取先取后排的思想可得符合要求的选法共有

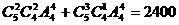　　　 (种)

3. 由数字1、2、3、4、5、6、7组成无重复数字的七位数.

(1)求有3个偶数相邻的7位数的个数；

(2)求3个偶数互不相邻的7位数的个数.

答案：用捆绑法可得(1)为720个；用插空法可得(2)为1440个.

2.一名数学教师和四名获奖学生排成一行留影，若老师不排在两端，则共有_____种不同的排法.

分析：(法一)、从特殊元素出发，由于数学教师是特殊元素，所以他除了两端外，还有3个位置可排共有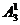种排法，然后排学生共有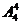种排法，由分步计数原理可得答案是72.

(法二)从特殊位置出发，由于两端是特殊位置，除数学教师外先从四名学生中选2人排在两端共有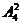种排法，然后剩余的学生及老师排剩余的位置共有A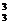种排法.由分步计数原理可得答案是72.