9. ．(4分)①扣合材料信息，突出音乐会某一特点(2分)；②合情合理(1分)；③语言简明生动(1分)。

4. 图示法

由波的传播方向确定质点的振动方向的方法有多种，但最简单、最直观的方法还是“图示法”，因为波的传播方向与质点的振动方向存在着非常简单的图示关系，如图6所示。

用此法判断时，须取正半周或负半周波形，以取正半周为例，由于峰点不振动，而两侧的质点振动反向，要求表示传播方向的箭头要与峰点相切，于是表示质点振动方向的箭头与表示波传播方向的箭头间必有：“箭头跟箭头相对”或“箭尾跟箭尾相对”的关系，负半周同理。为便于记忆，可简记为“头头相对”或“尾尾相对”。

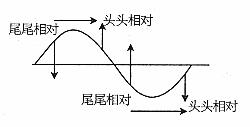
图6

例3. 已知一列简谐横波沿x轴正方向传播，如图7所示，试标明此时刻a、b、c、d各质点的振动方向。

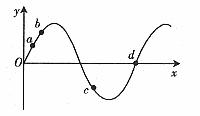
图7

解析：由“头头相对”或“尾尾相对”可知，各质点的振动方向如图8所示。

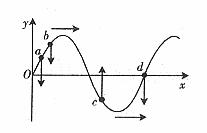
图8

例4. 已知一列简谐横波如图9所示，此时刻P点的振动方向沿y轴正方向，试标明波的传播方向。

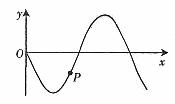
图9

解析：由“尾尾相对”可知，此波沿x轴负方向传播，如图10所示。

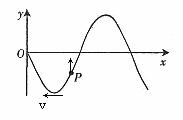
图10

3. 观察法(也称波形法)

将简谐波的波形想象成一条凹凸起伏的“坡路”，当沿着波的传播方向行走时，在“上坡”段各质点的振动方向向下；在“下坡”段各质点的振动方向向上。可简单记为“上坡向下，下坡向上”。这种方法简捷、直观，应用更广泛。

解析：“观察法”：通过前两种方法得到的结果可看出，沿波的传播方向看去，图象“上坡”段的质点均向上振动，而“下坡”段的质点向上振动，如图4所示，由此结论可快速判定质点振动方向(或波的传播方向)。

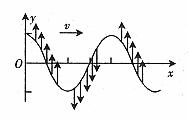
图4

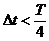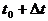若已知某质点振动方向而要求判断波的传播方向，仍可利用上述思想方法得出“微振法”，即将已知振动方向的质点(如图5中的M点)沿其振动方向作一微小运动()，找到时刻M的位置M'，再过M'作波形图，从波峰的移动方向(以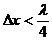为准)即可确定波的传播方向(图5中波的传播方向向左)。当然也可直接用“观察法”。

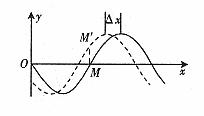
图5

2. 特殊点法

在质点P靠近波源一方附近(不超过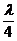)图象上找另一点P'，若P'在P上方则P向上运动，若P'在P下方则P向下运动。

例2. 题目同例1。

解析：特殊点法：由于沿波的传播方向，后一质点(远离波源的质点)总是重复前一质点(靠近波源的质点)的振动，但在时间上滞后，故可在M的前面(靠近波源一方)附近(不超过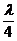)找到另一质点P，由M重复但滞后于P的振动可知M此时刻应向下(y轴负方向)运动，如图3所示。

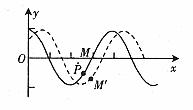
图3

1. 微平移法

作出经微小时间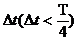后的波形，就知道了各质点经过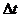时间到达的位置，运动方向就知道了。

例1. 已知一列沿x轴正方向传播的简谐横波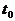时刻的波形如图1实线所示，判断该时刻质点M的振动方向。

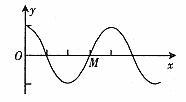
图1

解析：微平移法，将波沿其传播方向平移一小段距离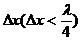，如图2的虚线所示，这对应着质点M在其平衡位置O'附近振动了一小段时间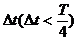后到达M'点，故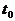时刻质点M正在沿y轴负方向振动。

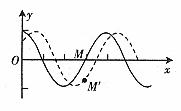
图2

8．(05年连云港)一个矩形线圈在一匀强磁场中绕垂直于磁场方向的中心轴匀速转动，产生的交变电动势表达式为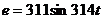V，试求：

(1)电动势的最大值、有效值和频率；

(2)若矩形线圈是100匝，线圈平面面积为0.02m²，匀强磁场的磁感应强度B是多少?

(3)当线圈平面从中性面开始转过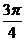时，电动势的瞬时值是多大?

答案：(1)将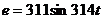(V)　跟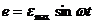对应比较，可知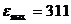V　　

有效值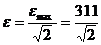：　 V＝220V　

频率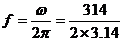：　 Hz＝50Hz

(2)由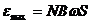得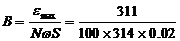T＝0.5T　　

(3)线圈从中性面转过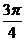，即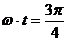　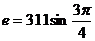　　 V＝311×0.707V＝220V

7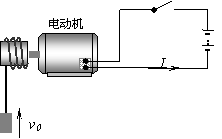．(05年宿迁)如图所示，是用直流电动机提升重物的装置示意图，电源电动势E＝100V，内电阻r₁＝1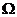，电动机的线圈电阻r₂＝4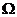。重物质量m＝36kg，重物被电动机以v＝0.5m/s的速度匀速提起，不计重物运动中所受的阻力，取g＝10m/s²，试求：电路中的电流I和电源的输出功率P。

答案：电源的输出功率：P＝UI　 由闭合电路欧姆定律　E＝U+Ir₁　 即　P＝I(E－Ir₁)　

电动机的热功率：P_热＝I ²r₂ 　电动机的输出机械功率：P_出＝mgv　则：P＝mgv+I ²r₂

所以得：I²(r₂+r₁)－IE+mgv＝0　　 代入数据化简，得：I ²－20I+36＝0

所以I＝2(A)　(I＝18A舍去)　　　　　　 得P＝196(W)

6．(05年南通)如图所示，电源的电动势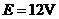，内阻不计，电阻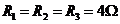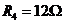，，电容器的电容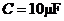，其中有一带电微粒恰好处于静止状态。若在工作的过程中，电阻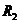突然发生断路。电流表可看作理想电表。求：

(1)带电微粒加速度的大小和方向。

(2)从电阻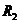断路到电路稳定的过程中，流经电流表的电量。

答案：(1)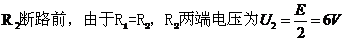　

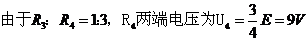
电容器两端电压为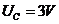，带电量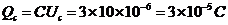(上板带负电)

带电微粒静止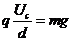　　　

断路后，电路稳定后，电容器两端电压，

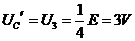电容器带电量为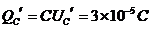(上板带正电)　　

带电微粒的加速度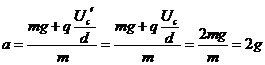，方向竖直向下。　

(2)从电阻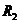断路到电路稳定的过程中，流经电流表的电量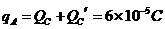

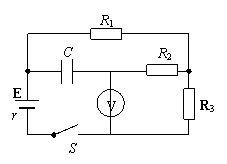
5．(06年南京)所示电路中，电源电动势E=10V，内阻r=1Ω，电容器电容C=40μF，电阻R₁=R₂=4Ω，R₃=5Ω。接通电键S，待电路稳定后，求：

(1)理想电压表V的读数；

(2)电容器的带电量。

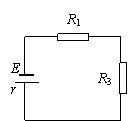答案：当开关合上后，等效电路如图所示，这时电压表测得　 的是R₃两端的电压U₃，电容器两端的电压为R₁两端的电压U₁

(1)流过电路中的总电流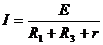

代入数据得I=1A　　 U₃=IR₃ U₃=5V

(2)U₁=IR₁ U₁=4V　　 C=Q/U₁ Q=CU=1.6×10 ^-4C

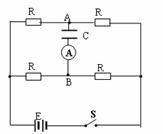
4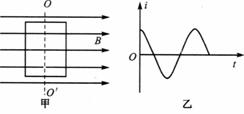．如图甲所示，一矩形闭合线圈在匀强磁场中绕垂直于磁场方向的转轴ΟΟ′以恒定的角速度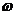转动，当线圈平面与磁场方向平行时开始计时，线圈中产生的交变电流按照图乙所示的余弦规律变化．在 t=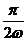时刻 　(　 CD　 )

A．线圈中的电流最大

B．穿过线圈的磁通量为零

C．线圈所受安培力的力矩为零

D．线圈消耗的电功率为零