
1.(2002全国文,7)椭圆5x2+ky2=5的一个焦点是(0,2),那么k等于( )
A.-1
B.1
C.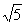 D.
-
D.
-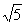
2(2002全国文,11)设θ∈(0,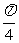 ),则二次曲线x2cotθ-y2tanθ=1的离心率的取值范围为( )
),则二次曲线x2cotθ-y2tanθ=1的离心率的取值范围为( )
A.(0,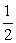 ) B.(
) B.(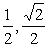 ) C.(
) C.(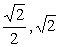 )
D.(
)
D.(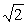 ,+∞)
,+∞)
3(2002北京文,10)已知椭圆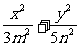 和双曲线
和双曲线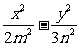 =1有公共的焦点,那么双曲线的渐近线方程是(
)
=1有公共的焦点,那么双曲线的渐近线方程是(
)
A.x=±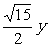 B.y=±
B.y=±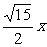 C.x=±
C.x=±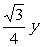 D.y=±
D.y=±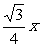
4(2002京皖春,13)若双曲线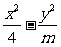 =1的渐近线方程为y=±
=1的渐近线方程为y=±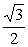 x,则双曲线的焦点坐标是 .
x,则双曲线的焦点坐标是 .
5(2002全国文,16)对于顶点在原点的抛物线,给出下列条件:
①焦点在y轴上;
②焦点在x轴上;
③抛物线上横坐标为1的点到焦点的距离等于6;
④抛物线的通径的长为5;
⑤由原点向过焦点的某条直线作垂线,垂足坐标为(2,1).能使这抛物线方程为y2=10x的条件是 .(要求填写合适条件的序号)
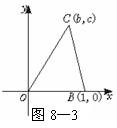 例1(2002北京,21)已知O(0,0),B(1,0),C(b,c)是△OBC的三个顶点.如图8-3.
例1(2002北京,21)已知O(0,0),B(1,0),C(b,c)是△OBC的三个顶点.如图8-3.
(Ⅰ)写出△OBC的重心G,外心F,垂心H的坐标,并证明G、F、H三点共线;
(Ⅱ)当直线FH与OB平行时,求顶点C的轨迹.
例2.(2002江苏,20)设A、B是双曲线x2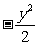 =1上的两点,点N(1,2)是线段AB的中点.
=1上的两点,点N(1,2)是线段AB的中点.
(Ⅰ)求直线AB的方程;
(Ⅱ)如果线段AB的垂直平分线与双曲线相交于C、D两点,那么A、B、C、D四点是否共圆,为什么?
例3(2002上海,18)已知点A(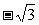 ,0)和B(
,0)和B(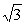 ,0),动点C到A、B两点的距离之差的绝对值为2,点C的轨迹与直线y=x-2交于D、E两点,求线段DE的长.
,0),动点C到A、B两点的距离之差的绝对值为2,点C的轨迹与直线y=x-2交于D、E两点,求线段DE的长.
例4(2003上海春,21)设F1、F2分别为椭圆C: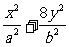 =1(a>b>0)的左、右两个焦点.
=1(a>b>0)的左、右两个焦点.
(1)若椭圆C上的点A(1, )到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
)到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
(2)设点K是(1)中所得椭圆上的动点,求线段F1K的中点的轨迹方程;
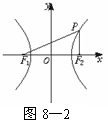 (3)已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值.试对双曲线
(3)已知椭圆具有性质:若M、N是椭圆C上关于原点对称的两个点,点P是椭圆上任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,那么kPM与kPN之积是与点P位置无关的定值.试对双曲线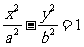 写出具有类似特性的性质,并加以证明.
写出具有类似特性的性质,并加以证明.
3.(2002京皖春,3)已知椭圆的焦点是F1、F2,P是椭圆上的一个动点.如果延长F1P到Q,使得|PQ|=|PF2|,那么动点Q的轨迹是( )
A.圆 B.椭圆 C.双曲线的一支 D.抛物线
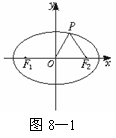 4(2003京春,16)如图8-1,F1、F2分别为椭圆
4(2003京春,16)如图8-1,F1、F2分别为椭圆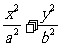 =1的左、右焦点,点P在椭圆上,△POF2是面积为
=1的左、右焦点,点P在椭圆上,△POF2是面积为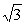 的正三角形,则b2的值是_____.
的正三角形,则b2的值是_____.
5(2003上海春,4)直线y=x-1被抛物线y2=4x截得线段的中点坐标是_____.
6(2002上海春,2)若椭圆的两个焦点坐标为F1(-1,0),F2(5,0),长轴的长为10,则椭圆的方程为 .
2.(2003京春理,7)椭圆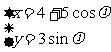 (
(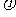 为参数)的焦点坐标为( )
为参数)的焦点坐标为( )
A.(0,0),(0,-8) B.(0,0),(-8,0)
C.(0,0),(0,8) D.(0,0),(8,0)
1.(2003京春文9,理5)在同一坐标系中,方程a2x2+b2y2=1与ax+by2=0(a>b>0)的曲线大致是( )
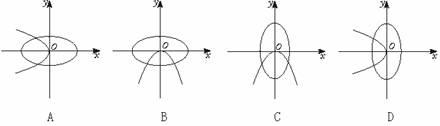
12.如图所示装置是医生给病人输液用的普通输液器.在输液时,A管与空气相连,B管下面连接一小容器C,然后再用皮管连接到注射器,溶液沿皮管下流到容器C中被隔断(C内有少量的空气),并以液滴形式下滴,再经皮管和注射器进入人体.试分析:
(1)容器C的作用.
(2)设输液瓶口到注射针头D的平均高度h为70 cm,人体血管内血液的平均压强约为一个大气压,普通人注射用针头的内径为0.3 mm,并假设液体流动时,所受粘滞等阻力为重力的1/2,试估算注射500 mL盐水所需的时间.(g取10 m/s2)
答案 (1)用来观察输液的快慢 (2)45分钟
11.我国陆地面积S=960万平方千米,若地面大气压p0=1.0×105 Pa,地面附近重力加速度g取10 m/s2,空气平均摩尔质量为M0=3.0×10-2 kg·mol-1,阿伏加德罗常数NA=6×1023 mol-1,试估算:
(1)我国陆地上空空气的总质量M总.
(2)我国陆地上空空气的分子总数n总.
(3)地面附近温度为270 K的1 m3空气,在温度为300 K时的体积.
 答案 (1)9.6×1016
kg (2)1.9×1042
(3)1.1 m3
答案 (1)9.6×1016
kg (2)1.9×1042
(3)1.1 m3
10.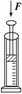 如图是用导热性能良好的材料制成的气体实验装置,开始时封闭的空气柱长度为22 cm,现用竖直向下的外力F压缩气体,使封闭的空气柱长度变为2 cm,人对活塞做功100 J,大气压强为p0=1×105
Pa,不计活塞的重力.问:
如图是用导热性能良好的材料制成的气体实验装置,开始时封闭的空气柱长度为22 cm,现用竖直向下的外力F压缩气体,使封闭的空气柱长度变为2 cm,人对活塞做功100 J,大气压强为p0=1×105
Pa,不计活塞的重力.问:
(1)若用足够长的时间缓慢压缩,求压缩后气体的压强有多大?
(2)若以适当的速度压缩气体时,向外散失的热量为20 J,则气体的内能增加多少?(活塞的横截面积S=1 cm2)
答案 (1)1.1×106 Pa (2)82 J
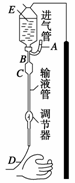
9.如图所示为一种测定“肺活量”(标准大气压下人一次呼出气体的体积)的装置,A为开口薄壁圆筒,排尽其中的空气,倒扣在水中.测量时,被测者尽力吸足空气,再通过B管用力将气体吹入A中,使A浮起.设整个过程中呼出气体的温度保持不变.
(1)呼出气体的分子热运动的平均动能 (填“增大”、“减小”或“不变”).
(2)设圆筒A的横截面积为S,大气压强为p0,水的密度为 ,桶底浮出水面的高度为h,桶内外水面的高度差为Δh,求被测者的“肺活量”.
,桶底浮出水面的高度为h,桶内外水面的高度差为Δh,求被测者的“肺活量”.
答案 (1)不变 (2)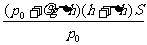
8.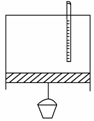 某校开展探究性课外活动,一同学用如图所示的装置研究气体压强、体积、温度三量之间的变化关系.该同学选用导热良好的气缸将其开口向下,内有理想气体,并将气缸固定不动,缸内活塞可自由滑动且不漏气.把一温度计通过缸底小孔插入缸内,插口处密封良好,活塞下挂一个沙桶,沙桶装满沙子时,活塞恰好静止,现给沙桶底部钻一个小洞,让细沙慢慢漏出,外部环境温度恒定,则( )
某校开展探究性课外活动,一同学用如图所示的装置研究气体压强、体积、温度三量之间的变化关系.该同学选用导热良好的气缸将其开口向下,内有理想气体,并将气缸固定不动,缸内活塞可自由滑动且不漏气.把一温度计通过缸底小孔插入缸内,插口处密封良好,活塞下挂一个沙桶,沙桶装满沙子时,活塞恰好静止,现给沙桶底部钻一个小洞,让细沙慢慢漏出,外部环境温度恒定,则( )
A.外界对气体做功,内能增大
B.外界对气体做功,温度计示数不变
C.气体体积减小,温度计示数减小
D.外界对气体做功,温度计示数增加
答案 B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com