
2.例2.已知三棱柱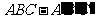 的底面为直角三角形,两直角边
的底面为直角三角形,两直角边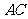 和
和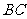 的长分别为
的长分别为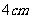 和
和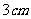 ,侧棱
,侧棱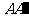 的长为
的长为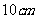 ,求满足下列条件的三棱柱的体积:
,求满足下列条件的三棱柱的体积:
(1)
侧棱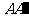 垂直于底面;
垂直于底面;
(2)
侧棱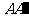 与底面所成的角为
与底面所成的角为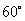 .
.
解:(1)因为侧棱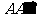 底面
底面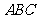 ,所以三棱柱的高
,所以三棱柱的高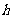 等于侧棱
等于侧棱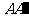 的长,而底面三角形
的长,而底面三角形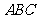 的面积
的面积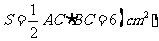 ,于是三棱柱的体积
,于是三棱柱的体积
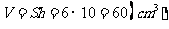 .
.
(2)如图所示,过 作平面
作平面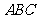 的垂线,垂足为
的垂线,垂足为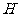 ,
,
 于是
于是 为三棱柱的高.因为侧棱
为三棱柱的高.因为侧棱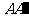 与底面所成的角为
与底面所成的角为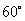 ,所以
,所以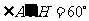 ,可计算得
,可计算得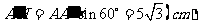
又由(1)可知底面三角形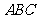 的面积
的面积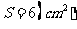 ,故三棱柱的体积
,故三棱柱的体积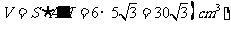
1.引例的解答:这是一个底面是梯形的直四棱柱的体积问题.
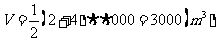 .
.
8.祖暅原理的简单应用:
(1) 底面积和高都相等的圆柱和长方体的体积相等吗?
(2) 底面积和高都相等的斜六棱柱和三棱锥的体积相等吗?
7. 介绍祖冲之父子及我国古代数学家和西方数学家对几何体体积的研究:
中国古代数学,在魏晋南北朝达到新的高峰.这一时期的代表人物是刘徽(公元263年左右)、祖冲之(429-500)和他的儿子祖暅.刘徽为《九章算术》作注,祖冲之父子在此基础上撰写了《缀术》等著作.祖冲之精确地计算圆周率,提出约率和密率,是世界数学史上的重大成就.他们三人还先后研究并最终给出了球的体积公式.在这过程中,他们利用了“夫叠棊成立积,缘幂势既同,则积不容异”的原理,唐朝的李淳风在为《九章算术》作注时称求球体体积公式的方法是“祖暅之开立园术”,祖暅之即祖暅,因此我国称之为祖暅原理.意大利数学家卡瓦列里1635年提出了相同的原理,西方称之为卡瓦列里原理,为微积分学创立作了准备.
6. 利用祖暅原理推导棱柱体积公式:
(1)利用祖暅原理推导棱柱体积,需要构造一个几何体,此几何体必须符合两个条件: 它的计算公式是已知的;
它的计算公式是已知的; 它符合祖暅原理的条件,即该几何体与棱柱能夹在两个平行平面之间,且用平行于这两个平面的任意一个平面去截它们时,截得的截面面积总相等.
它符合祖暅原理的条件,即该几何体与棱柱能夹在两个平行平面之间,且用平行于这两个平面的任意一个平面去截它们时,截得的截面面积总相等.
(2)方法:如果一个棱柱与一个长方体的高相同(都为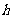 )且底面面积相等(都为
)且底面面积相等(都为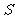 ),那么当我们用一个与底面平行的平面去截它们时,可以证明截面的面积都等于各自底面的面积
),那么当我们用一个与底面平行的平面去截它们时,可以证明截面的面积都等于各自底面的面积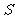 ,根据祖暅原理可知,棱柱的体积与长方体的体积相等,即
,根据祖暅原理可知,棱柱的体积与长方体的体积相等,即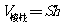 ,其中
,其中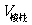 表示棱柱的体积,
表示棱柱的体积,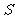 表示棱柱底面的面积,
表示棱柱底面的面积,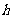 表示棱柱的高.
表示棱柱的高.
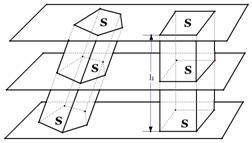
5.祖暅原理:“夫叠棊成立积,缘幂势既同,则积不容异”.
(1)内容解释:这里的“幂”是指水平截面的面积,“势”是指高.
即体积可看成是由面积叠加而成,用一组平行平面截两个空间图形,若在任意等高处的截面面积都对应相等,则两空间图形的体积必然相等.
还可表达为:夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.(我国古代数学家祖暅在实践的基础上,明确肯定了这一点)
(2)由“面积都相等”推出“体积相等”,体会辩证法的思想.
(3)祖暅原理实际上是一个定理,但证明它需要用到高等数学的相关知识,中学阶段不能证明.它只能判定两个几何体是否等积,不能用它具体求出某几何体的体积.要想完成求体积的任务,还必须已知一个几何体的体积作为基础.
(4)几何画板动态演示任意一个平面截两个几何体所得截面的各种位置.
4.祖暅原理的引入--利用“小试验”验证以上猜想:
(1)取一叠裁切相同的纸张堆放在水平桌面上,然后用手推一下以改变其形状.
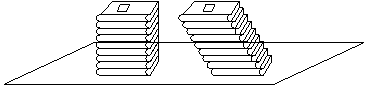
启发思考:
1) 推斜以后体积变化了吗?(几何体所占空间的大小不变)
2) 推斜前后的两个几何体(前为长方体,后为平行六面体)还有什么共同之处?(高度没有改变,每页纸张的顺序和面积也没有改变)
3) 这种共同之处是不是就是两个几何体体积相等的条件呢?
(2)用一摞不同的书,推移成各种形状,继续探讨结论是否正确.(不一定是棱柱)
(3)由学生总结归纳出祖暅原理的大致内容.
3.从平面到空间的类比猜想:(利用几何画板的动态演示)
(1)等底等高的长方形和平行四边形的面积有何关系?
(2)等底等高的三角形的面积有何关系?
(3)等底等高的梯形的面积有何关系?
结论:根据面积公式我们可以得到面积均相等.初中我们学过的面积公式的推导是因为任意平面多边形(直边形)都可以用割补的方法转化为长方形的面积得到.在利用几何画板动态演示的过程中,我们发现,用平行于底边的任意直线截两个平面图形得到的截线长度总相等.
启发思考:这是否可以成为两个平面图形面积相等的条件呢?
继续探究:线是由无穷多个点构成的,面是由无穷多条线构成的,立体是由无穷多个平面构成的.因此我们可以得到:夹在两条平行直线之间的两个平面图形,被平行于这两条直线的任意直线所截,如果所得的两条截线长度相等,那么,这两个平面图形的面积相等.
猜想:类比到两个空间图形体积相等的条件有什么相似的结论呢?用平行于底面的任意平面截两个空间图形得到的截面面积总相等,则这两个空间图形的体积相等.
2.进一步考虑正方体、长方体的体积公式的来龙去脉:
(1)请学生谈谈对体积的理解,并小结:几何体占空间部分的大小叫做它的体积.
(2) 提问:体积是如何度量的?(类比长度的度量和面积的度量)
学生讨论后小结:
1)我们在度量长度时,有一个标准,比如说,1米,1厘米等;将一段线段用1厘米来截,看这个线段是1厘米的多少个倍数,就是这个线段有多少厘米.5倍就是5厘米,1.5倍就是1.5厘米.
2)在度量面积时,也有一个标准,比如说1平方米即边长为1米的正方形作为1个单位面积,去度量平面图形的面积.因此,我们容易得到正方形的面积等于棱长的平方,长方形的面积等于底乘以高.因为任意多边形都可以分割成若干个三角形,三角形可以补成平行四边形,平行四边形可以割补成长方形,所以任意平面多边形的面积都可以度量.(直边形)
3)在体积中,我们也要先选定一个单位,用来度量体积,然后求出几何体是单位体积的多少倍,多少个倍数就是几何体的体积数值.通常把棱长等于单位长度的正方体所占空间的大小作为一个体积单位.只要直接把单位正方体尽可能地堆在所量的几何体内,来确定所量几何体的体积的量数.因此我们容易得到正方体和长方体的体积公式,但是不容易得到一般棱柱的体积公式.(可以先把一般棱柱分割成三棱柱,三棱柱补成平行六面体,平行六面体割补成长方体)
4)如何找到长方体的体积和一般棱柱的体积之间的关系?
1.从已知到未知,从特殊到一般:
首先想到已经学过的正方体、长方体的体积公式,然后探究一般棱柱的体积公式.
(1)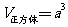 (
(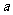 -棱长);
-棱长);
(2)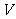 长方体
长方体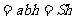 (
(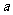 -长,
-长,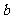 -宽,
-宽,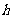 -高,
-高,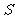 -底面积)
-底面积)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com