
6.数列的递推公式:如果已知数列的第一项(或前几项)及相邻两项(或几项)间关系可以用一个公式来表示,则这个公式就叫做这个数列的递推公式.递推公式是给出数列的一种重要方法,其关健是先求出a1,a2,然后用递推关系逐一写出数列中的项.
5. 无穷数列:项数无限的数列叫做无穷数列
4. 有穷数列:项数有限的数列叫做有穷数列.
3.通项公式:一般地,如果数列{an}的第n项与序号n之间的关系可以用一个公式来表示,那么这个公式叫做这个数列的通项公式.
2.项:数列中的每一个数都叫做这个数列的项,各项依次叫做这个数列的第1项(或首项),第2项,…,第n项,….
1.数列:按一定次序排成的一列数叫做数列.
在初中几何中我们曾经学过“点到直线的距离以垂线为最短。”此结论对于求极小值问题,是一条捷径。
例6如图1-1所示,船A从港口P出发去拦截正以速度υ0沿直线航行的船B 。P与B所在航线的垂直距离为a,A起航时与B船相距为b,b>a 。如果略去A船起动时的加速过程,认为它一起航就匀速运动。则A船能拦截到B船的最小速率为多少?
 分析与解:分析本题是两个运动物体求它们之间的相对位置的问题。若以地球为参照系,两个物体都运动,且运动方向不一致,它们之间的相对位置随时间变化的关系比较复杂,一时不容易做出正确的判断与解答。但如果把参照系建立在某一运动的物体上,(如B上)由于以谁为参照系,就认为谁不动,此题就简化为一个物体,(如A)在此运动参照系的运动问题了。当然解一个物体的运动问题比解两个物体都运动的问题自然容易多了。
分析与解:分析本题是两个运动物体求它们之间的相对位置的问题。若以地球为参照系,两个物体都运动,且运动方向不一致,它们之间的相对位置随时间变化的关系比较复杂,一时不容易做出正确的判断与解答。但如果把参照系建立在某一运动的物体上,(如B上)由于以谁为参照系,就认为谁不动,此题就简化为一个物体,(如A)在此运动参照系的运动问题了。当然解一个物体的运动问题比解两个物体都运动的问题自然容易多了。
 以B为参照系,B不动,在此参照系中A将具有向左的分速度υ0,如图1-2所示。在此参照系中A只要沿着PB方向就能拦截到B 。应用“点到直线的距离以垂线为最短”的结论。过O点作PB的垂线,交PB于E点,OE即为A船对地的速度的最小值υA,在△AOE中
以B为参照系,B不动,在此参照系中A将具有向左的分速度υ0,如图1-2所示。在此参照系中A只要沿着PB方向就能拦截到B 。应用“点到直线的距离以垂线为最短”的结论。过O点作PB的垂线,交PB于E点,OE即为A船对地的速度的最小值υA,在△AOE中
∵υA=υ0Sinθ 而  ∴
∴ ,由于灵活运用了几何知识,使较为复杂的问题,变为简单的几何问题了。
,由于灵活运用了几何知识,使较为复杂的问题,变为简单的几何问题了。
例7如图1-3所示,重为G的物体与水平地面的动摩擦因数为μ,欲以一个拉力F使物体沿地面匀速前进。问F与水平地面的夹角θ为何值时最省力?这个最小拉力是多大? 分析与解:画出物体的受力分析图,如图1-4所示。物体受到四个力的作用。有重力G、拉力F、地面的支持力N及地面对物体的滑动摩擦力f,其中f=Nμ。这四个力为共点力,合力为零。可将N与f合成为一个力N′,N与f的作用将被N′等效,N′与N、f的关系满足平行四边形法则。再画出物体受N′、G、F的力的矢量三角形,如图1-5所示。N′的方向如图,应用“点到直线的距离以垂线为最短”的结论。过B点作N′的垂线交N′于C点,则BC的长度即表示最小作用力Fmin,由于Fmin与水平面夹角为θ,




∴∠CAB=∠θ Fmin=Gsinθ
由图1-6可知,
 即
即 θ=arctanμ
几何法一般用于求极小值问题,其特点是简单、直观,把物体运动的较为复杂的极值问题,转化为简单的几何问题去解,便于学生掌握。
以上求极值的方法是解高中物理题的常用方法。在使用中,还要注意题目中的条件及“界”的范围。求最大和最小值问题,这类问题往往是物理学公式结合必要的数学知识才得出结论,这就要求学生不仅理解掌握物理概念、规律,还要具备较好的运用数学解决问题的能力。
解决极值问题的关键是扎实掌握高中物理的基本概念,基本规律,在分析清楚物理过程后,再灵活运用所学的数学知识。
综上所述,无论采用何种方法解物理极值问题,首先都必须根据题意,找出符合物理规律的物理方程或物理图象,这也是解决物理问题的核心,决不能盲目地将物理问题纯数学化。
θ=arctanμ
几何法一般用于求极小值问题,其特点是简单、直观,把物体运动的较为复杂的极值问题,转化为简单的几何问题去解,便于学生掌握。
以上求极值的方法是解高中物理题的常用方法。在使用中,还要注意题目中的条件及“界”的范围。求最大和最小值问题,这类问题往往是物理学公式结合必要的数学知识才得出结论,这就要求学生不仅理解掌握物理概念、规律,还要具备较好的运用数学解决问题的能力。
解决极值问题的关键是扎实掌握高中物理的基本概念,基本规律,在分析清楚物理过程后,再灵活运用所学的数学知识。
综上所述,无论采用何种方法解物理极值问题,首先都必须根据题意,找出符合物理规律的物理方程或物理图象,这也是解决物理问题的核心,决不能盲目地将物理问题纯数学化。
(二)利用“化一”法求三角函数极值。对于复杂的三角函数,例如
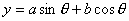 ,要求极值时,先需要把不同名的三角函数
,要求极值时,先需要把不同名的三角函数 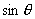 和
和
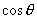 ,变成同名的三角函数,这个过程叫做“化一”。
,变成同名的三角函数,这个过程叫做“化一”。
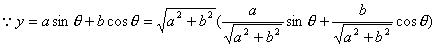
令 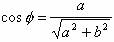 ,则有
,则有
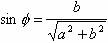
y
y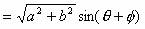
故 y的极大值为  。
。
例题4 物体放置在水平地面上,物理与地面之间的动摩擦因数为μ,物体重为G,欲使物体沿水平地面做匀速直线运动,所用的最小拉力F为多大?
该题的已知量只有 μ和G,说明最小拉力的表达式中最多只含有μ和G,但是,物体沿水平地面做匀速直线运动时,拉力F可由夹角的不同值而有不同的取值。因此,可根据题意先找到F与夹角有关的关系式再作分析。
解:设拉力 F与水平方向的夹角为θ,根据题意可列平衡方程式,
即 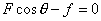 ……①
……①
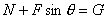 ……②
……②
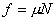 …………③
…………③
由联立①②③解得:
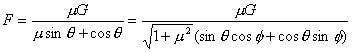
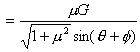 ,
,
其中 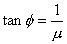 ,∴
,∴ 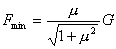
四 利用向量求极值
向量就是物理学中的矢量,当物体受三力平衡时,将三矢量首尾相连后,必定构成三角形。利用点到直线的垂直线段最短可求极值。
 对于例题 4,我们也可用矢量知识求极值。
对于例题 4,我们也可用矢量知识求极值。
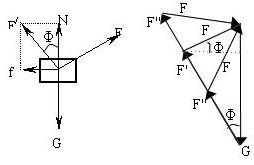
将摩擦力 f和地面对木块的弹力N合成一个力F',如图,F'与竖直方向的夹角为
 (为一定值)。这样木块可认为受到三个力:重力G,桌面对木块的作用力F'和拉力F的作用。尽管F大小方向均未确定,F'方向一定,但大小未定,但三力首尾相连后必构成三角形,如右图所示。只用当F与F'垂直时,即拉力与水平方向成
(为一定值)。这样木块可认为受到三个力:重力G,桌面对木块的作用力F'和拉力F的作用。尽管F大小方向均未确定,F'方向一定,但大小未定,但三力首尾相连后必构成三角形,如右图所示。只用当F与F'垂直时,即拉力与水平方向成 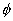 角时,拉力F最小为
角时,拉力F最小为 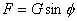
而 
故 
五 用图像法求极值
通过分析物理过程遵循的物理规律,找到变量之间的函数关系,做出其图像,由图像可求得极值。
例 5 从车站开出的汽车作匀加速运动,它开出一段时间后,突然发现有乘客未上车,于是立即制动做匀减速运动,结果汽车从开动到停下来共用20秒,前进了50米。求这过程中汽车达到的最大速度。
解:设最大速度为 V m ,即加速阶段的末速度为V m 。
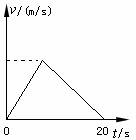 画出其速度时间图象如右图所示,图线与 t轴围成的面积等于位移。即
画出其速度时间图象如右图所示,图线与 t轴围成的面积等于位移。即
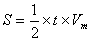
即: 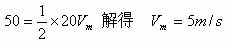
(一)利用三角函数的有界性求极值
如果所求物理量表达式中含有三角函数,可利用三角函数的有界性求极值。若所求物理量表达式可化为“ 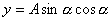 ”的形式,可变为
”的形式,可变为
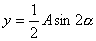 ,
,
当 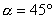 时,
时,
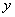 有极值
有极值
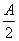 。
。
例 3如图所示,底边恒定为b,当斜面与底边所成夹角θ为多大时,物体沿此光滑斜面由静止从顶端滑到底端所用时间才最短?
此题的关键是找出物体从斜面顶端滑至底端所用时间与夹角的关系式 ,这是一道运动学和动力学的综合题,应根据运动学和动力学的有关知识列出物理方程。
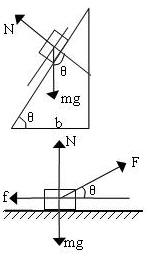 解:设斜面倾角为θ时,斜面长为 S,物体受力如 图所示,由图知
解:设斜面倾角为θ时,斜面长为 S,物体受力如 图所示,由图知
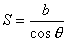 …………………①
…………………①
由匀变速运动规律得:  …………②
…………②
由牛顿第二定律提: mgsinθ=ma…………③
联立①②③式解得:
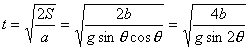
可见,在 90°≥θ≥0°内,当2θ=90°时,sin2θ有最大值,t有最小值。
即θ =45°时,有最短时间为: 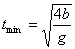
(二)如果a,b,c为正数,则有 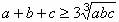 ,当且仅当a=b=c时,上式取“=”号。
,当且仅当a=b=c时,上式取“=”号。
推论:
1.三个正数的积一定时,三数相等时,其和最小。
2.三个正数的和一定时,三数相等时,其积最大。
例 2一轻绳一端固定在O点,另一端拴一小球,拉起小球使轻绳水平,然后无初速度的释放,如图所示,小球在运动至轻绳达到竖直位置的过程中,小球所受重力的瞬时功率在何处取得最大值?
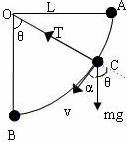 解:当小球运动到绳与竖直方向成θ角的 C时,重力的功率为:
解:当小球运动到绳与竖直方向成θ角的 C时,重力的功率为:
P=mgυcosα=mgυsinθ…………①
小球从水平位置到图中 C位置时,机械能守恒有:
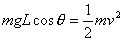 ……………②
……………②
解①②可得: 
令 y=cosθsin2θ

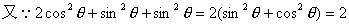
根据基本不等式
 ,定和求积知:
,定和求积知:
当且仅当
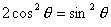 ,y有最大值
,y有最大值
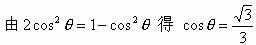
由此我们可以得出结论:当
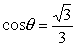 时,y及功率P有最大值。
时,y及功率P有最大值。
三 利用三角函数求极值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com