
1.已知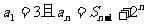 ,求
,求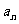 及
及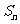 。
。
[例1]已知数列1,4,7,10,…,3n+7,其中后一项比前一项大3.(1)指出这个数列的通项公式;(2)指出1+4+…+(3n-5)是该数列的前几项之和.
错解:(1)an=3n+7;
(2) 1+4+…+(3n-5)是该数列的前n项之和.
错因:误把最后一项(含n的代数式)看成了数列的通项.(1)若令n=1,a1=10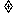 1,显然3n+7不是它的通项.
1,显然3n+7不是它的通项.
正解:(1)an=3n-2;
(2) 1+4+…+(3n-5)是该数列的前n-1项的和.
[例2]
已知数列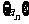 的前n项之和为①
的前n项之和为① 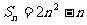 ②
② 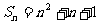

求数列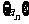 的通项公式。
的通项公式。
错解: ① 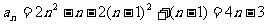

② 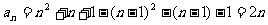

错因:在对数列概念的理解上,仅注意了an=Sn-Sn-1与的关系,没注意a1=S1.
正解: ①当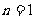 时,
时,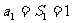

当 时,
时,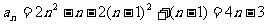

经检验
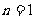 时
时 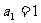 也适合,
也适合,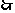
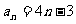

②当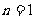 时,
时,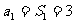

当 时,
时,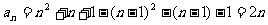

∴ 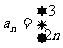
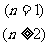

[例3] 已知等差数列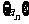 的前n项之和记为Sn,S10=10 ,S30=70,则S40等于
。
的前n项之和记为Sn,S10=10 ,S30=70,则S40等于
。
错解:S30= S10·2d. 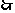 d=30,
d=30, 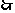 S40= S30+d =100.
S40= S30+d =100.
错因:将等差数列中Sm, S2m -Sm,
S3m -S2m成等差数列误解为Sm, S2m,
S3m成等差数列.
正解:由题意: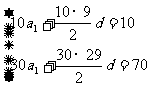 得
得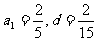

代入得S40 =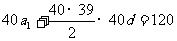 。
。
[例4]等差数列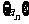 、
、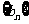 的前n项和为Sn、Tn.若
的前n项和为Sn、Tn.若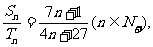 求
求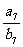 ;
;
错解:因为等差数列的通项公式是关于n的一次函数,故由题意令an=7n+1;bn=4n+27.
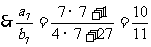

错因:误认为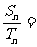
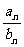

正解: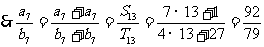

[例5]已知一个等差数列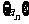 的通项公式an=25-5n,求数列
的通项公式an=25-5n,求数列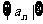 的前n项和;
的前n项和;
错解:由an 0得n
0得n 5
5
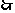
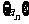 前5项为非负,从第6项起为负,
前5项为非负,从第6项起为负,
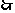 Sn=a1+a2+a3+a4+a5=50(n
Sn=a1+a2+a3+a4+a5=50(n 5)
5)
当n 6时,Sn=|a6|+|a7|+|a8|+…+|an|=
6时,Sn=|a6|+|a7|+|a8|+…+|an|=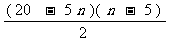

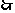 Sn=
Sn=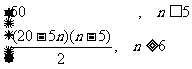

错因:一、把n 5理解为n=5,二、把“前n项和”误认为“从n
5理解为n=5,二、把“前n项和”误认为“从n 6起”的和.
6起”的和.
正解: 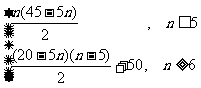

[例6]已知一个等差数列的前10项的和是310,前20项的和是1220,
由此可以确定求其前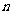 项和的公式吗?
项和的公式吗?
解:理由如下:由题设: 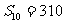
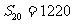

得: 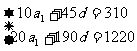
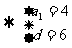

∴ 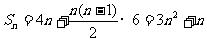

[例7]已知: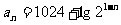 (
(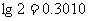 )
)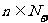 (1) 问前多少项之和为最 大?(2)前多少项之和的绝对值最小?
(1) 问前多少项之和为最 大?(2)前多少项之和的绝对值最小?
解:(1) 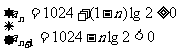
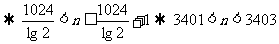 ∴
∴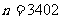

(2)


当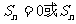 近于0时其和绝对值最小
近于0时其和绝对值最小
令: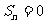 即 1024+
即 1024+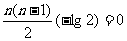

得: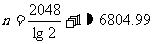

∵ 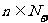 ∴
∴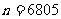

[例8]项数是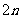 的等差数列,中间两项为
的等差数列,中间两项为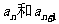 是方程
是方程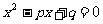 的两根,求证此数列的和
的两根,求证此数列的和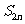 是方程
是方程 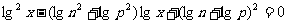 的根。 (
的根。 (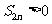 )
)
证明:依题意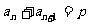

∵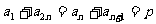 ∴
∴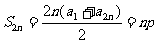

∵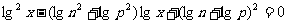

∴ 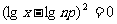 ∴
∴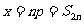 (获证)。
(获证)。 
6、在解决等差数列问题时,如已知,a1,an,d,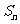 ,n中任意三个,可求其余两个。
,n中任意三个,可求其余两个。
5、对等差数列的前n项之和公式的理解:等差数列的前n项之和公式可变形为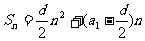 ,若令A=
,若令A=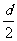 ,B=a1-
,B=a1-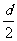 ,则
,则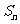 =An2+Bn.
=An2+Bn.
4.从函数的角度考查等差数列的通项公式:an=
a1+(n-1)d=d·n+ a1-d, an是关于n的一次式;从图像上看,表示等差数列的各点(n,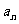 )均匀排列在一条直线上,由两点确定一条直线的性质,不难得出,任两项可以确定一个等差数列.
)均匀排列在一条直线上,由两点确定一条直线的性质,不难得出,任两项可以确定一个等差数列.
3.数列{an}的前n项的和Sn与an之间的关系: 若a1适合an(n>2),则
若a1适合an(n>2),则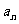 不用分段形式表示,切不可不求a1而直接求an.
不用分段形式表示,切不可不求a1而直接求an.
2.一个数列的通项公式通常不是唯一的.
1.数列的概念应注意几点:(1)数列中的数是按一定的次序排列的,如果组成的数相同而排列次序不同,则就是不同的数列;(2)同一数列中可以出现多个相同的数;(3)数列看做一个定义域为正整数集或其有限子集({1,2,3,…,n})的函数.
8.等差中项:如果a,A,b这三个数成等差数列,那么A=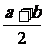 .我们把A=
.我们把A=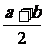 叫做a和b的等差中项.
叫做a和b的等差中项. 
7.等差数列:一般地,如果一个数列从第二项起,每一项减去它的前一项所得的差都等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用d表示.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com