
(一)如果a,b为正数,那么有:
 ,当且仅当a=b时,上式取“=”号。
,当且仅当a=b时,上式取“=”号。
推论:
1.两个正数的积一定时,两数相等时,其和最小。
2.两个正数的和一定时,两数相等时,其积最大。
(三)利用配方法求极值
对于二次函数 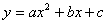 ,函数解析式经配方可变为
,函数解析式经配方可变为
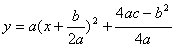
(1)若a>0时,当 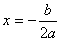 时,y有极小值为
时,y有极小值为 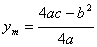
(2)若a<0时,当 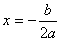 时,y有极大值为
时,y有极大值为 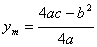
对于例题 1还可用配方法求解。
(二)利用一元二次方程判别式求极值
对于二次函数y = ax2 + bx + c,(a ≠0)可变形为一元二次方程
ax2 + bx + c - y=0
用判别式法 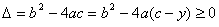 即:
即:
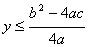
则由不等式可知 y的极值为: 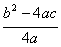
对于例题 1,我们可以转化为二次方程求解。
将 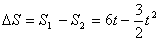 可转化为一元二次方程:
可转化为一元二次方程:
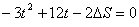
要使方程有解,必使判别式 
解不等式得: 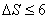 ,即最大值为6m
,即最大值为6m
例1.一个质量为m的电子与一个静止的质量为M的原子发生正碰,碰后原子获得一定速度,并有一定的能量E被贮存在这个原子内部。求电子必须具有的最小初动能是多少?
分析与解:设电子碰前的速度为υ1,碰后的速度为 ,静止的原子被碰后的速度为
,静止的原子被碰后的速度为 。
由动量守恒定律有
。
由动量守恒定律有 (1)
由能量守恒有
(1)
由能量守恒有 (2)
在以上两个方程中,有三个未知数,υ1、
(2)
在以上两个方程中,有三个未知数,υ1、 、
、 ,一般的同学认为少一个方程,难以求解。但由(1)式解出
,一般的同学认为少一个方程,难以求解。但由(1)式解出 代入(2)
可得:
代入(2)
可得: 进一步整理可得:(M+m)m
进一步整理可得:(M+m)m -2m2υ1
-2m2υ1 +(m-M)mυ12+2ME=0
此式是关于
+(m-M)mυ12+2ME=0
此式是关于 的一元二次方程,因电子碰后的速度
的一元二次方程,因电子碰后的速度 必为实数,所以此方程的判别式B2-4AC≥0 即
4m4
必为实数,所以此方程的判别式B2-4AC≥0 即
4m4 -4(M+m)m[(m-M)m
-4(M+m)m[(m-M)m +2ME]≥0
根据上式整理可得:
+2ME]≥0
根据上式整理可得: 所以电子必须具有的最小的初动能是
所以电子必须具有的最小的初动能是
例2.如图2-1所示,顶角为2θ的光滑圆锥,置于磁感应强度大小为B,方向竖直向下的匀强磁场中,现有一个质量为m,带电量为+q的小球,沿圆锥面在水平面作匀速圆周运动,求小球作圆周运动的轨道半径。 分析与解:小球在运动时将受重力mg,圆锥面对球的弹力N,及洛仑兹力f的作用,如图2-2所示。设小球作匀速圆周运动的轨道半径为R,速率为υ。


由正交分解可得 联立(1)、(2)试可得
联立(1)、(2)试可得
 上式有υ、R两个未知量,似乎不可解,但因为是求极值问题,可用一元二次方程判别式求解。因为υ有实数解,由B2-4AC≥0
即
上式有υ、R两个未知量,似乎不可解,但因为是求极值问题,可用一元二次方程判别式求解。因为υ有实数解,由B2-4AC≥0
即  ∴小球作圆周运动的最小半径为
∴小球作圆周运动的最小半径为
例3.在掷铅球的运动中,如果铅球出手时距地面的高度为h,速度为υ0,求υ0与水平方向成何角度时,水平射程最远?并求此最大的水平射程Xmax。
分析与解:以出手点为坐标原点,可分别列出水平方向与竖直方向的位移方程。
 上式为关于tgθ的一元二次方程。若tgθ存在实数解,则判别式B2-4AC≥0
即
上式为关于tgθ的一元二次方程。若tgθ存在实数解,则判别式B2-4AC≥0
即  解出结果后,我们可联系实际进行如下验证。设出手高度h=0,
则
解出结果后,我们可联系实际进行如下验证。设出手高度h=0,
则 θ=45°。这就是我们过去曾经知道的一个物体做斜抛运动,当θ=45°时其射程最远。
θ=45°。这就是我们过去曾经知道的一个物体做斜抛运动,当θ=45°时其射程最远。
(二)用二次函数极值公式求极值。
对于典型的一元二次函数y = ax2 + bx + c,(a ≠0)
若a > 0, 则当 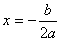 时 ,y 有极小值,为 ymin=
时 ,y 有极小值,为 ymin=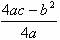 ;
;
若 a < 0, 则当 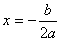 时 ,y 有极大值,为 ymax=
时 ,y 有极大值,为 ymax=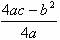 。
。
例 1 一辆汽车在十字路口等候绿灯,当绿灯亮时汽车以 3m/s 2 的加速度开始行驶。恰在这时一辆自行车以 6m/s 的速度匀速驶来,从后边赶过汽车。汽车从路口开动后,在追上自行车之前过多长时间两车相距最远?此时距离是多少?
分析:根据题意,自行车做匀速运动,汽车做匀加速运动。汽车与自行车的位移之差是一个关于时间的二次函数,所以可以用二次函数极值公式求极值。
解:经过时间 t后,自行车做匀速运动,其位移为S1=Vt,
汽车做匀加速运动,其位移为: 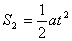
两车相距为: 
这是一个关于 t的二次函数,因二次项系数为负值,故ΔS有最大值。
当 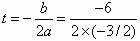 =2(s)时ΔS有最大值。
=2(s)时ΔS有最大值。

在解物理问题时,若列出的物理方程满足二次函形式,则可由求二次函数极值的方法求解物理极值。主要有以下几种类型:
44.下图为我国某区域等温线图,表格为乙地区气候资料图,完成下列要求。 (8分)
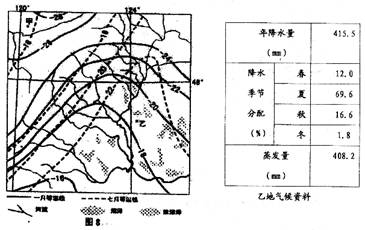
(1)简述该地一月份等温线的分布特征。
(2)甲地与乙地纬度仅相差2度,但气温差异却很大,试分析甲地冬季气温低的原因。

43.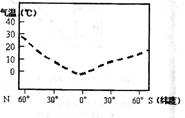 读各纬度平均气温年较差示意图,同答下列问题。
读各纬度平均气温年较差示意图,同答下列问题。
(1)气温年较差的分布规律是 ,有
此规律的原因是 。
(2)60°N与60°S相比,平均气温年较差 更
大,有此现象的原因是 。
(3)我国各地的气温年较差的分布规律是 。
(提示:注意(2)题的思路)
42.读我国东部地区不同月份的雨带图,完成下列问题。(14分)
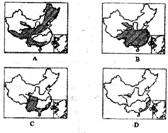 (1)按雨带推移的时间顺序,将A、B、C、D
(1)按雨带推移的时间顺序,将A、B、C、D
重新排序为 。
(2)雨带的推移主要是由 风的进退决
定的,雨带的降雨类型属于 雨。
(3)据图说明我国南方雨季和北方雨季长短的
差别。
(4)与“黄梅时节家家雨,青草池塘处处蛙”
的景象对应的是 图,与华北平原春旱对应的是 图,与伏早天气对应的是一图。
41.读下图,按要求完成下列各小题。(8分)
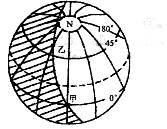
(1)该图表示的是每年 (节气)日的情况,此刻太阳直射点的地理坐标
是 , 。
(2)图中,甲乙两地均位于晨昏线中的 线上,乙地日出时刻是 点钟。
(3)按图中所示情况,北京时间是 点钟,我国南极昆仑考察站的黑夜长 小时。
(4)在图中所示的这一天,下列地点中正午太阳高度角最大的是( )
A.北京 B.广州 C.甲地 D.乙地
(5)按图中所示,如果是晴天,过64小时后能看到北极星的有下列地点中的( )
A.北京 B.纽约 C.莫斯科 D.悉尼
降水量的分布。读图7,回答39-40题.
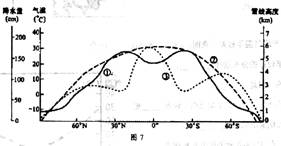
39.表示多年平均雪线高度、气温、降水量的曲线依次是
A:①②③ B.①③② C.③②① D.③①②
40.多年平均雪线高度
A.随纬度增高而降低 B.在副热带地区最高
C.在降水量大的地区较高 D.在南半球低纬度地区最低
第Ⅱ卷(非选择题,共40分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com