8.在函数y＝f(x)的图象上有点列{x_n，y_n}，若数列{x_n}是等差数列，数列{y_n}是等比数列，则函数y＝f(x)的解析式可能为　　　　　　　　　　　　　　　　　　　　 (　)

A.f(x)＝2x+1 　　　B.f(x)＝4x² C.f(x)＝log₃x　 　　　　　D.f(x)＝()^x

解析：结合选项，对于函数f(x)＝()^x上的点列{x_n，y_n}，有y_n＝()x_n.由于{x_n}是等差数列，所以x_n+1－x_n＝d，因此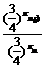＝＝()x_n+1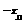＝()^d，这是一个与n无关的常数，故{y_n}是等比数列.

答案：D

7.在数列{a_n}中，a₁＝1，a₂＝2，a_n+2－a_n＝1+(－1)ⁿ，那么S₁₀₀的值等于　　　 (　)

A.2500　 　　　B.2600　　　　　 C.2700　 　　　　　　D.2800

解析：据已知当n为奇数时，

a_n+2－a_n＝0⇒a_n＝1，

当n为偶数时，a_n+2－a_n＝2⇒a_n＝n，

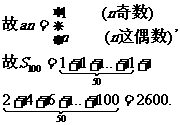
答案：B

6.定义：在数列{a_n}中，a_n＞0且a_n≠1，若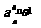为定值，则称数列{a_n}为“等幂数列”.已知数列{a_n}为“等幂数列”，且a₁＝2，a₂＝4，S_n为数列{a_n}的前n项和，则S₂₀₀₉＝　　　　　　　　　　　　　　　

(　)

A.6026　 　　　　　B .6024　　　　　　　 C.2　　　　　　　　　 　D.4

解析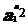：＝2⁴＝16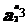＝＝4a₃，

得a₃＝2，同理得a₄＝4，a₅＝2，…，

这是一个周期数列.

∴S₂₀₀₉＝×(2+4)+2＝6026.

答案：A

答案：B

5.记数列{a_n}的前n项和为S_n，且S_n＝2n(n－1)，则该数列是　　　　　　　　　 (　)

A.公比为2的等比数列　　　　　　　 B.公比为的等比数列

C.公差为2的等差数列　　　　　　　 D.公差为4的等差数列

解析：由条件可得n≥2时，a_n＝S_n－S_n－1＝2n(n－1)－2(n－1)(n－2)＝4(n－1)，当n＝1时，a₁＝S₁＝0，代入适合，故a_n＝4(n－1)，故数列{a_n}表示公差为4的等差数列.

答案：D

4.在等差数列{a_n}中，若a₂+a₄+a₆+a₈+a₁₀＝80，则a₇－·a₈的值为　　　　　　 (　)

A.4　 　　　　　B.6　　　　　　 C.8 　　　　　　　D.10

解析：由已知得：(a₂+a₁₀)+(a₄+a₈)+a₆＝5a₆＝80⇒a₆＝16，又分别设等差数列首项为a₁，公差为d，则a₇－a₈＝a₁+6d－(a₁+7d)＝(a₁+5d)＝a₆＝8.

答案：C

3.已知{a_n}是等差数列，a₄＝15，S₅＝55，则过点P(3，a₃)，Q(4，a₄)的直线斜率为(　)

A.4 　　　　　B.　　　　　　 C.－4　　　　　　　 　D.－

解析：∵{a_n}是等差数列，

∴S₅＝5a₃＝55，∴a₃＝11.

∴a₄－a₃＝15－11＝4，

∴k_PQ＝＝＝4.

答案：A

2.等差数列{a_n}的通项公式是a_n＝1－2n，其前n项和为S_n，则数列{}的前11项和为

(　)

A.－45　 　　　　B.－50　　　　 C.－55　　　　　 　D.－66

解析：S_n＝，∴＝＝－n，

∴{}的前11项的和为－66.

答案：D

1.已知实数列－1，x，y，z，－2成等比数列，则xyz等于　　　　　　　　　 (　)

A.－4　　　　B.±4　　　　　　 C.－2 　　　　　　　　D.±2

解析：∵xz＝(－1)×(－2)＝2，y²＝2，∴y＝－(正不合题意)，∴xyz＝－2.

答案：C

21.(本小题满分14分)已知函数f(x)＝(x²－3x+3)·e^x的定义域为[－2，t](t>－2)，设f(－2)＝m，f(t)＝n.

(1)试确定t的取值范围，使得函数f(x)在[－2，t]上为单调函数；

(2)求证：n>m；

解：(1)因为f′(x)＝(x²－3x+3)·e^x+(2x－3)·e^x＝x(x－1)·e^x，

由f′(x)>0⇒x>1或x<0；由f′(x)<0⇒0<x<1，

所以f(x)在(－∞，0)，(1，+∞)上单调递增，在(0,1)上单调递减，

欲使f(x)在[－2，t]上为单调函数，则－2<t≤0.

(2)因为f(x)在(－∞，0)，(1，+∞)上单调递增，在(0,1)上单调递减，所以f(x)在x＝1处取得极小值f(1)＝e.

又f(－2)＝<e，所以f(x)仅在x＝－2处取得[－2，t]上的最小值f(－2)，

从而当t>－2时，f(－2)<f(t)，即m<n.

20.(本小题满分13分)定义在R上的函数f(x)满足f(x)＝f(x+4)，当2≤x≤6时，f(x)＝

()^|x－m|+n，f(4)＝31.

(1)求m，n的值；

(2)比较f(log₃m)与f(log₃n)的大小.

解：(1)因为函数f(x)在R上满足f(x)＝f(x+4)，

所以4是函数f(x)的一个周期.

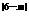可得f(2)＝f(6)，即()+n＝()+n，　　　　　　　　　　　　　　　 ①

又f(4)＝31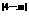，()+n＝31，　　　　　　　　　　　　　　　　　　　　　 ②

联立①②组成方程组解得m＝4，n＝30.

(2)由(1)知，函数f(x)＝()+30，x∈[2,6].

因为1<log₃4<2，所以5<log₃4+4<6.

f(log₃m)＝f(log₃4)＝f(log₃4+4)

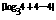＝()+30

＝()^|log₃^4|+30.

又因为3<log₃30<4，