
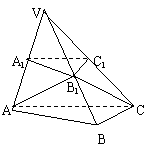
7. (2006山东)如图,已知平面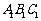 平行于三棱锥
平行于三棱锥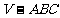 的底面ABC,等边△
的底面ABC,等边△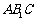 所在的平面与底面ABC垂直,且∠ACB=90°,设
所在的平面与底面ABC垂直,且∠ACB=90°,设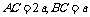
(1)求证直线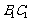 是异面直线
是异面直线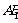 与
与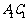 的公垂线;
的公垂线;
(2)求点A到平面VBC的距离;
(3)求二面角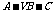 的大小.
的大小.

证明(Ⅰ)∵平面
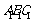 ∥平面
∥平面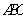 ,
,
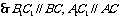
∵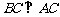 ∴
∴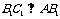
又∵平面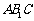 ⊥平面
⊥平面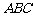 ,平面
,平面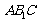 ∩平面
∩平面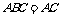 ,∴
,∴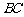 ⊥平面
⊥平面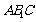 ,
,
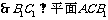
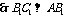 ,
,
又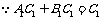 ,
,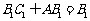 .
.
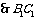 为
为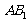 与
与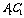 的公垂线.
的公垂线.
解(Ⅱ):过A作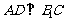 于D,
于D,
∵△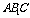 为正三角形,∴D为
为正三角形,∴D为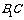 的中点.
的中点.
∵BC⊥平面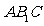 ∴
∴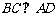 ,
,
又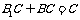 ,∴AD⊥平面
,∴AD⊥平面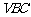 ,
,
∴线段AD的长即为点A到平面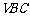 的距离.
的距离.
在正△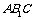 中,
中,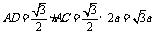 .
.
∴点A到平面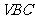 的距离为
的距离为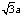 .
.
解法2:取AC中点O连结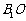 ,则
,则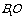 ⊥平面
⊥平面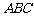 ,且
,且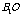 =
=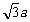 .
.
由(Ⅰ)知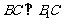 ,设A到平面
,设A到平面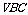 的距离为x,
的距离为x,
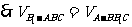 ,
,
即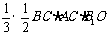
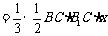 ,
,
解得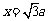 .即A到平面
.即A到平面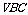 的距离为
的距离为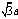 .
.
则
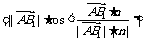
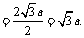
∴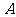 到平面
到平面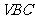 的距离为
的距离为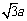 .
.
(III)过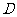 点作
点作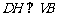 于
于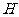 ,连
,连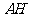 ,由三重线定理知
,由三重线定理知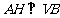
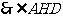 是二面角
是二面角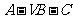 的平面角.
的平面角.
在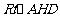 中,
中,
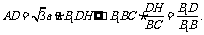
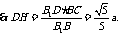
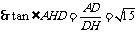 .
.
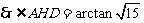 .
.
所求二面角大小为arctan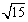 .
.
5. 4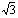 192π; 6.距离为12.
192π; 6.距离为12.
[解答题]
6.已知球面上的三点A、B、C,AB=6,BC=8,AC=10,球的半径为13,则球心到平面ABC的距离为 .
◆答案提示: 1-3.ACC; 4. 1∶3∶5;
5.(2004年北京)地球仪上北纬30°纬线的长度为12πcm,该地球仪的半径是_________cm,表面积是_________cm2.
4.过棱锥高的三等分点作两个平行于底面的截面,它们将棱锥的侧面分成三部分的面积的比(自上而下)为__________.
3.各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是( )
A.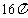 B.
B.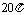 C.
C.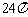 D.
D.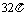
[填空题]
2.长方体的一个顶点上三条棱长为3、4、5,且它的八个顶点都在一个球面上,这个球的表面积是 ( )
A.20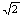 π B.25
π B.25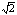 π C.50π D.200π
π C.50π D.200π
1.P是长方体AC1上底面A1C1内任一点,设AP与三条棱AA1、AB、AD所成的角为α、β、γ,则cos2α+cos2β+cos2γ的值是 ( )
A.1 B.2 C. 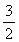 D.不确定
D.不确定
4.要正确地区别球面上两点间的直线距离与球面距离.搞清纬度、经度、纬度差、经度差等概念.
同步练习 9.6棱柱、棱锥和球
[选择题]
3.球的概念和性质以及面积、体积是解决有关问题的重要依据;它的轴截面是解决问题的重要“场所”,球半径、截面圆半径、圆心距都在这个图形内,它把空间问题转化为平面问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com