
5.已知集合P={(x,y)||x|+|y|=1},Q={(x,y)|x2+y2≤1},则P与Q的关系为 .
答案 P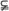 Q
Q
4.集合A={y∈R|y=lgx,x>1},B={-2,-1,1,2},则( RA)∩B= .
RA)∩B= .
答案 {-2,-1}
3.设全集U=R,集合M={x|x≤1或x≥3},集合P=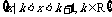 ,且
,且 UM
UM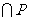 ≠
≠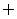 ,则实数k的取值
,则实数k的取值
范围是 .
答案 0<k<3
2.已知全集U={0,1,3,5,7,9},A∩ UB={1},B={3,5,7},那么(
UB={1},B={3,5,7},那么( UA)∩(
UA)∩( UB)=
.
UB)=
.
答案 {0,9}
1.(2008·江西理,2)定义集合运算:A*B=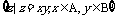 设A=
设A=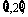 B
B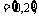 则集合A*B
则集合A*B
的所有元素之和为 .
答案 6
12.在区间[0,1]上给定曲线y=x2,试在此区间内确定点t的值,使图中阴影部分的面积S1与S2之和最小.
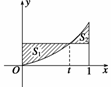 解 S1面积等于边长为t与t2的矩形面积去掉曲线y=x2与x轴、直线x=t所围成的面积,即
解 S1面积等于边长为t与t2的矩形面积去掉曲线y=x2与x轴、直线x=t所围成的面积,即
S1=t·t2-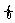 x2dx=
x2dx=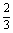 t3.
t3.
S2的面积等于曲线y=x2与x轴、x=t,x=1围成的面积减去矩形面积,
矩形边长分别为t2,(1-t),即
S2=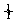 x2dx-t2(1-t)=
x2dx-t2(1-t)=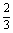 t3-t2+
t3-t2+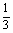 .
.
所以阴影部分的面积S为
S=S1+S2=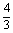 t3-t2+
t3-t2+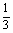 (0≤t≤1).
(0≤t≤1).
∵S′(t)=4t2-2t=4t(t-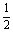 )=0时,得t=0,t=
)=0时,得t=0,t=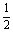 .
.
当t=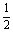 时,S最小,∴最小值为S(
时,S最小,∴最小值为S(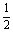 )=
)=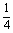 .
.
11.如图所示,抛物线y=4-x2与直线y=3x的两交点为A、B,点P在抛物线上从A向B运动.
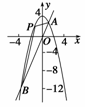 (1)求使△PAB的面积最大的P点的坐标(a,b);
(1)求使△PAB的面积最大的P点的坐标(a,b);
(2)证明由抛物线与线段AB围成的图形,被直线x=a分为面积相等的两部分.
(1)解 解方程组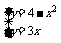 ,得x1=1,x2=-4.
,得x1=1,x2=-4.
∴抛物线y=4-x2与直线y=3x的交点为
A(1,3),B(-4,-12),
∴P点的横坐标a∈(-4,1).
点P(a,b)到直线y=3x的距离为d=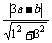 ,
,
∵P点在抛物线上,∴b=4-a2,
 =
=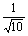 ·(4-3a-a2)′=
·(4-3a-a2)′=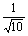 (-2a-3)=0,
(-2a-3)=0,
∴a=-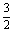 ,即当a=-
,即当a=-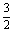 时,d最大,
时,d最大,
这时b=4-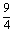 =
=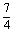 ,
,
∴P点的坐标为(-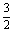 ,
,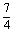 )时,△PAB的面积最大.
)时,△PAB的面积最大.
(2)证明 设上述抛物线与直线所围成图形的面积为S,
位于x=-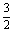 右侧的面积为S1.
右侧的面积为S1.
S=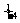 (4-x2-3x)dx=
(4-x2-3x)dx=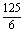 ,
,
S1=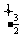 (4-x2-3x)dx=
(4-x2-3x)dx=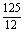 ,
,
∴S=2S1,即直线x=-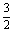 平分抛物线与线段AB围成的图形的面积.
平分抛物线与线段AB围成的图形的面积.
10.设函数f(x)=x3+ax2+bx在点x=1处有极值-2.
(1)求常数a,b的值;
(2)求曲线y=f(x)与x轴所围成的图形的面积.
解 (1)由题意知f′(x)=3x2+2ax+b,
f(1)=-2且f′(1)=0,
即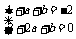 ,解得a=0,b=-3,
,解得a=0,b=-3,
即f(x)=x3-3x.
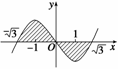 (2)作出曲线y=x3-3x的草图,所求面积为阴影部分的面积,由x3-3x=0得曲线y=x3-3x与x轴的交点坐标是(-
(2)作出曲线y=x3-3x的草图,所求面积为阴影部分的面积,由x3-3x=0得曲线y=x3-3x与x轴的交点坐标是(-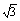 ,0),(0,0)和(
,0),(0,0)和(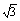 ,0),而y=x3-3x是R上的奇函数,函数图象关于原点中心对称.
,0),而y=x3-3x是R上的奇函数,函数图象关于原点中心对称.
所以(-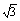 ,0)的阴影面积与(0,
,0)的阴影面积与(0, 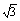 )的阴影面积相等.
)的阴影面积相等.
所以所求图形的面积为
S=2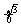 [0-(x3-3x)]dx
[0-(x3-3x)]dx
=-2(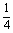 x4-
x4-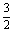 x2)|
x2)|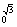 =
=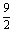 .
.
9.证明:把质量为m(单位:kg)的物体从地球的表面升高h(单位:m)处所做的功W=G·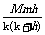 ,其中G是地球引力常数,M是地球的质量,k是地球的半径.
,其中G是地球引力常数,M是地球的质量,k是地球的半径.
证明 根据万有引力定律:知道对于两个距离为r,质量分别为m1、m2的质点,它们之间的引力为f(r)=G·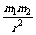 ,其中G为引力常数.
,其中G为引力常数.
则当质量为m的物体距地面高度为x(0≤x≤h)时,地心对它的引力f(x)=G·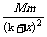 .
.
故该物体从地面升到h高处所做的功为
W=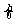 f(x)dx=
f(x)dx=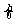 G·
G·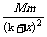 ·dx
·dx
=GMm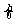
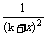 d(k+x)
d(k+x)
=GMm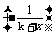 |
|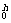
=GMm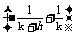
=G·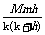 .
.
8.若f(x)是一次函数,且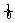 f(x)dx=5,
f(x)dx=5, 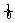 xf(x)dx=
xf(x)dx=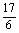 ,那么函数f(x)的解析式是
.
,那么函数f(x)的解析式是
.
答案 f(x)=4x+3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com